Círculo de Mohr
El círculo de Mohr es una técnica usada en ingeniería y geofísica para representar gráficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tensiones, adaptando los mismos a las características de una circunferencia (radio, centro, etc.). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.
Este método fue desarrollado hacia 1882 por el ingeniero civil alemán Christian Otto Mohr (1835-1918).
Circunferencia de Mohr para esfuerzos
Caso bidimensional

En dos dimensiones, la Circunferencia de Mohr permite determinar la compresión máxima y mínima, a partir de dos mediciones de la tensión normal y tangencial sobre dos ángulos que forman 45°:
- NOTA: El eje vertical se encuentra invertido, por lo que esfuerzos positivos van hacia abajo y esfuerzos negativos se ubican en la parte superior.
Usando ejes rectangulares, donde el eje horizontal representa la tensión normal y el eje vertical representa la tensión cortante o tangencial para cada uno de los planos anteriores. Los valores de la circunferencia quedan representados de la siguiente manera:
- Centro del círculo de Mohr:
- Radio de la circunferencia de Mohr:
Las tensiones máxima y mínima vienen dados en términos de esas magnitudes simplemente por:
Estos valores se pueden obtener también calculando los valores propios del tensor tensión que en este caso viene dado por:
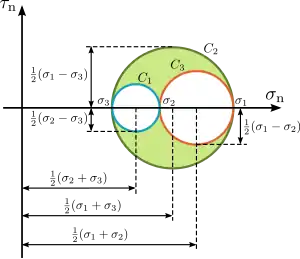
Caso tridimensional
Tensores esféricos y desviadores
Tensor Esférico
Dan lugar a cambios de volumen pero nunca de forma, es decir, su sentido físico es el de fuerzas de distintas direcciones convergentes hacia un mismo punto, como por ejemplo la presión que ejerce el agua a un objeto que se encuentra en las profundidades, la presión hace que el sistema se colapse hacía el interior.
Tensor Desviador Dan lugar a cambios de forma pero no de volumen. En algunos tipos de plasticidad la superficie de fluencia se calcula a partir del tensor desviador; no del tensor completo.
Circunferencia de Mohr para momentos de inercia
Para sólidos planos y casi-planos, puede aplicarse la misma técnica de la circunferencia de Mohr que se usó para tensiones en dos dimensiones. En muchas ocasiones es necesario calcular el momento de inercia alrededor de un eje que se encuentra inclinado, la circunferencia de Mohr puede ser utilizado para obtener este valor. También es posible obtener los momentos de inercia principales. En este caso las fórmulas de cálculo del momento de inercia medio y el radio de la circunferencia de Mohr para momentos de inercia son análogas a las del cálculo de esfuerzos:
- Centro de la circunferencia:
- Radio de la circunferencia: