Camino óctuple (física)
En física, el camino óctuple es un término acuñado por el físico estadounidense Murray Gell-Mann para una teoría que organiza los bariones y mesones en octetes (haciendo referencia al noble camino óctuple del budismo). La teoría fue propuesta independientemente por el físico israelí Yuval Ne'eman y condujo al posterior desarrollo del modelo de quarks.
Además de organizar los mesones y los bariones de espín 1/2 en un octete, los principios del camino óctuple también se aplican a los bariones de espín 3/2, que forman un decuplete. Sin embargo, una de las partículas de este decuplete nunca se había observado anteriormente. Gell-Mann llamó a esta partícula Ω− y predijo en 1962 que tendría extrañeza −3, carga eléctrica −1 y una masa cercana a 1680 MeV/c2. En 1964, un grupo del acelerador de partículas en Brookhaven descubrió una partícula de características muy próximas a estas predicciones.[1] Gell-Mann recibió en 1969 el premio Nobel de Física por su trabajo en la teoría de partículas elementales.
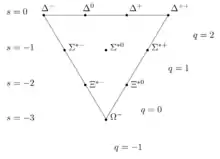
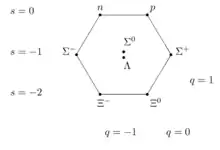

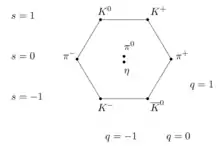
El camino óctuple se puede entender en términos modernos como consecuencia de las simetrías de sabor entre varias clases de quarks. Dado que la fuerza nuclear fuerte afecta a los quarks del mismo modo independientemente de su sabor; reemplazar un sabor de quark por otro en un hadrón no modifica mucho su masa. Matemáticamente, esta sustitución puede ser descrita por elementos del grupo SU(3). Los octetes y otros arreglos son representaciones de este grupo.[cita requerida]
Simetría de sabor
Hay un espacio vectorial tridimensional abstracto:
y las leyes de físicas son aproximadamente invariantes al aplicar una transformación unitaria de determinante 1 a este espacio (a veces llamada una rotación de sabor):
Aquí, SU(3) se refiere al grupo de Lie de matrices 3×3 unitarias con determinante 1 (grupo unitario especial). Por ejemplo, la rotación de sabor
es una transformación que simultáneamente convierte todos los quarks up en el universo a quarks down y viceversa. Más específicamente, estas rotaciones de sabor son simetrías exactas si solo se tienen en cuenta las interacciones fuertes, pero no son verdaderamente simetrías exactas del universo porque los tres quarks tienen masas diferentes y diferentes interacciones electrodébiles.
Esta la simetría aproximada se llama simetría de sabor, o más específicamente simetría de sabor SU(3).
(Esta es una descripción ligeramente simplificada de las rotaciones de sabor, ignorando anti-quarks etc.)
Conexión con la teoría de las representaciones
Supongamos que tenemos una partícula—por ejemplo, un protón—en un estado cuántico . Si aplicamos una de las rotaciones de sabor a nuestra partícula, se convierte en un nuevo estado cuántico . Dependiendo de A, este estado nuevo podría ser un protón, o un neutrón, o una superposición de un protón y un neutrón, o varias otras posibilidades. El conjunto de todos estados cuánticos posibles abarca un espacio vectorial.
La teoría de las representaciones es una teoría matemática que describe la situación donde elementos de un grupo (aquí, las rotaciones de sabor A en el grupo SU(3)) son automorfismos de un espacio vectorial (aquí, el conjunto de todos estados cuánticos posibles que se consiguen con rotaciones de sabor de un protón). Por tanto, estudiando la teoría de las representaciones de SU(3), podemos aprender cómo es el espacio vectorial y cómo está afectado por simetría de sabor.
Como las rotaciones de sabor son simetrías aproximadas, no exactas, cada estado ortogonal en el espacio vectorial corresponde a una especie de partícula diferente. En el ejemplo anterior, cuando un protón se transforma por cada rotación de sabor posible , resulta que se mueve en un espacio vectorial de dimensión 8. Estas 8 dimensiones corresponden a las 8 partículas en el "octete de bariones" (protón, neutrón, Σ+, Σ0, Σ−, Ξ−, Ξ0, Λ). Esto corresponde a una representación de dimensión 8 ("octete") del grupo SU(3). Dado que es una simetría aproximada, todas las partículas en este octete tienen masa similar.
Todo grupo de Lie tiene un álgebra de Lie correspondiente, y cada representación del grupo está relacionada con la correspondiente representación del álgebra de Lie en el mismo espacio vectorial. El álgebra (3) se puede escribir como el conjunto de matrices 3×3 Hermíticas de traza nula (matrices de Gell-Mann). Los físicos normalmente emplean la teoría de representaciones del álgebra de Lie (3) en lugar de la del grupo SU(3), ya que la primera es más simple, y las dos son equivalentes.
Desarrollo histórico
En el texto anterior, la simetría de sabor se define y motiva en términos del conocimiento moderno de los quarks. Pero históricamente fue al revés: los quarks estuvieron motivados por la simetría de sabor. Primero se descubrió que los grupos de partículas estaban relacionados entre sí de un modo que reproducía la teoría de representación de SU(3). De ahí se infirió que hay una simetría aproximada del universo qué es parametrizada por el grupo SU(3). Finalmente, esto condujo al descubrimiento de los quarks, tres de los cuales se intercambian en las transformaciones de SU(3) (los tres más ligeros: up, down y strange).[cita requerida]
Referencias
- V. E. Barnes (1964). «Observation of a Hyperon with Strangeness Minus Three». Physical Review Letters 12 (8): 204. Bibcode:1964PhRvL..12..204B. doi:10.1103/PhysRevLett.12.204.
- D. Griffiths (2008). Introduction to Elementary Particles 2nd.Ed. Wiley-VCH. ISBN 3527406018.ISBN 3527406018.
- M. Gell-Mann; Y. Ne'eman, eds. (1964). The Eightfold Way. W. A. Benjamin. LCCN 65013009. Archivado desde el original el 14 de julio de 2014. Consultado el 23 de marzo de 2016.LCCN 65013009.