Potencial de Yukawa

Hideki Yukawa demostró en los años 1930 que ese potencial aparece por el intercambio de campos escalares masivos. Este tipo de potencial tiene varias aplicaciones entre ellas, la interacción entre dos nucleones. Dos nucleones pueden experimentar interacción fuerte de tipo atractivo debido al intercambio de piones cargados, de una manera similar a como dos partículas interaccionan electromagnéticamente mediante intercambio de fotones. Así como el campo electromagnético es "transportado" por fotones, el campo piónico descrito por potencial de yukawa expresa es "transportado" por piones.

En la expresión del potencial de Yukawa como expresión de un campo piónico estático, la masa del pion ${\displaystyle m_{\pi }}$ es el parámetro que aparece en el exponente del potencial de Yukawa. Como el campo piónico mediador entre nucleones es masivo, la fuerza correspondiente tiene un cierto rango debido a su decaimiento, siendo el rango inversamente proporcional a la masa. La masa de los piones predice unas distancias típicas de actuación de la fuerza nuclear fuerte del orden del núcleo atómico. Es decir, el potencial de Yukawa aclaraba el porqué la fuerza nuclear fuerte tiene un alcance tan pequeño (del orden del núcleo atómico), ya que al ser las partículas mediadoras del campo masivas su intensidad tenía que decaer mucho más rápido que la ley de la inversa del cuadrado. Nótese que cuando las partículas mediadores tienen masa nula el exponente del potencial de Yukawa es cero y el potencial de Yukawa se convierte en un potencial de Coulomb, que posee un rango infinito y decae con la inversa del cuadrado.

En la ecuación dada, el potencial es negativo, denotando que la fuerza resultante es atractiva. La constante g es un número real llamada constante de acoplamiento entre el campo de mesones y el campo fermiónico con los que interactúa. En física nuclear, los fermiones pueden ser tanto el protón como el neutrón.

El potencial de Yukawa de un conjunto estacionario de partículas satisface la ecuación de Klein-Gordon:

${\displaystyle \left(\nabla ^{2}-{\frac {m^{2}c^{2}}{\hbar ^{2}}}\right)V(\mathbf {r} )=-g_{s}\delta (\mathbf {r} )}$

Para estimar el valor numérico de la intensidad de la fuerza nuclear pueden utilizarse los parámetros del Deuterón: alcance efectivo ${\displaystyle R\sim 2\,fm}$ y profundidad del pozo ${\displaystyle V_{0}\sim 30\,MeV}$ para dar:

${\displaystyle {\frac {g_{s}^{2}}{4\pi }}\sim 100\,MeV\cdot fm}$

Si se considera la constante de acoplamiento adimensionalizada se ve que:

${\displaystyle \alpha _{s}={\frac {g_{s}^{2}}{4\pi \hbar c}}\simeq 0.04}$.

Intercambio de un único mesón bosónico.

El potencial de Yukawa propiamente dicho sólo es una aproximación clásica a la interacción existente entre un par de fermiones que interactúan mediante un campo bosónico escalar. Puede demostrarse que da la amplitud de orden más bajo a la verdadera interacción entre dos fermiones que interactúan mediante intercambio de bosones escalares, es decir, la interacción de Yukawa acopla el campo fermiónico ${\displaystyle \psi (x)}$ a un campo mesónico ${\displaystyle \phi (x)}$ con un término asociado en el lagrangiano de la forma:

${\displaystyle {\mathcal {L}}_{\mathrm {int} }(x)=g{\overline {\psi }}(x)\phi (x)\psi (x).}$

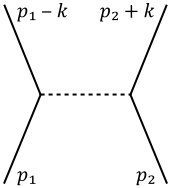
La amplitud de difusión para dos fermiones, uno con momento inicial ${\displaystyle p_{1}}$ y otro con momento ${\displaystyle p_{2}}$, que intercambiando un mesón de momento k, viene dada por el diagrama de Feynman mostrado a la derecha.

Las reglas de Feyman para cada vértice asocian un factor g con la amplitud, puesto que este diagrama tiene dos vértices, la amplitud total contendrá el factor ${\displaystyle g^{2}}$. La línea discontinua del medio que conecta las dos líneas fermiónicas (trazo continuo), representa al mesón intercambiado. La regla de Feynman para un intercambio de partícula es usar el propagador. El propagador de un mesón masivo es ${\displaystyle -4\pi /(k^{2}+m^{2})}$. Por tanto, la amplitud de Feynman para este grafo es precisamente:

${\displaystyle V(\mathbf {k} )=-g^{2}{\frac {4\pi }{k^{2}+m^{2}}}.}$

Esta amplitud, es precisamente, la transformada de Fourier del potencial de Yukawa.