Capacidad de penetración
La capacidad de penetración mide la distancia que un proyectil recorre dentro de un blanco antes de detenerse. El físico inglés Isaac Newton desarrolló por primera vez esta idea para obtener aproximaciones de la profundidad del impacto de proyectiles lanzados a altas velocidades.
- penetración
siendo
- Longitud del proyectil
- Densidad del proyectil
- Densidad del blanco
Como se aprecia en la fórmula no se tiene en cuenta la velocidad, pero no se debe olvidar que si la velocidad es baja no se puede aplicar la falta de cohesión. Tampoco depende del diámetro del proyectil.
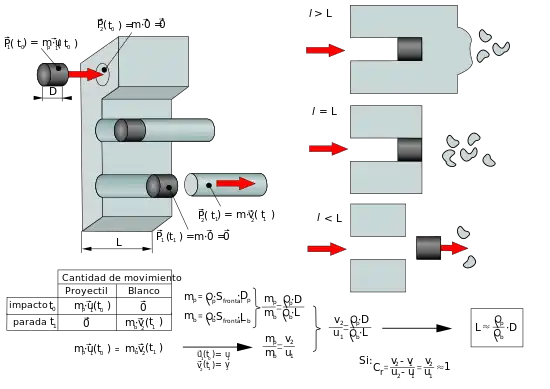
Si tenemos un blanco con un espesor menor que la capacidad de penetración el proyectil perderá parte de su velocidad por transferencia de cantidad de movimiento pero continuara aunque a menor velocidad. Si es espesor fuera justo la capacidad de penetración el proyectil se pararía justo antes de salir. Si el espesor es mayor el proyectil llegaría igualmente a hasta la capacidad de penetración. Hay que notar que según este modelo aunque se detenga el proyectil la parte del blanco desprendida tiene la misma cantidad de movimiento. En la realidad se producen deformaciones, desprendimiento de astillas, etc.
Aplicaciones
- Proyectil : El proyectil debe ser de un material metálico de alta densidad, tal como uranio 3) plomo 3) o wolframio 3). De acuerdo a la aproximación de Newton, un proyectil fabricado completamente de uranio perforará hasta aproximadamente 2.5 veces su propia longitud los blindajes de acero. Como es importante obtener una gran velocidad y una gran longitud se emplean proyectiles APFSDS con Sabot.
- Carga hueca: Para que una carga hueca (antitanque) perfore placas de acero. La carga tiene un hueco cónico recubierto de un metal denso como cobre o tantalio. Cuando explota este metal es impulsado para formar un chorro de metal a alta velocidad, donde los factores determinantes son que sea de gran densidad y longitud. Este chorro se mueve con lo que se puede considerar como el proyectil de la aproximación de Newton.
- Meteorito. Como puede concluirse de la presión del aire, el material de la atmósfera es equivalente a aproximadamente 10 m de agua. Ya que el hielo tiene aproximadamente la misma densidad que el agua, un trozo de hielo desde el espacio moviéndose a unos 15 km/s debe tener una longitud mayor de 10 m para alcanzar la superficie de la tierra a alta velocidad. Un trozo de hielo más pequeño se detendrá en pleno vuelo y explotará. Un trozo de hielo con un diámetro de 50 m o más, sin embargo, también se puede detener en el aire, siempre y cuando entre en un ángulo pequeño (por lo que debe atravesar un gran espesor de la atmósfera). El evento de Tunguska se explica a veces de esta manera. Un meteorito de hierro con un diámetro de 1.3 m penetrará la atmósfera, pero uno más pequeño se detendrá en el aire, y, finalmente, caerá en caída libre por la atracción gravitatoria llegando a la superficie con su velocidad terminal. La Piedra Negra, por ejemplo, con un diámetro de esta categoría.
- Revienta búnkeres . Una masa del impactador podrá utilizarse en lugar de una ojiva nuclear para penetrar búnkeres. De acuerdo a la aproximación de Newton, un proyectil de uranio de 1 m de longitud, moviéndose a alta velocidad llegaría a perforar 6 m de roca (con una densidad de3g/cm3), antes de detenerse. Un impactador de este tipo a una velocidad de 5-15 km/s, tiene más energía cinética que la contenida por una ojiva explosiva de la misma masa en forma de energía química.
Bibliografía
- Young, C.W. (1967). The Development of Empirical Equations for Predicting Depth of an Earth Penetrating Projectile (Report). SC-DR-67-60. Albuquerque NM: Sandia National Laboratories.
- Alekseevskii, V. P. (1966). «Penetration of a Rod into a Target at High Velocity». Combustion, Explosion, and Shock Waves (Fizika Goreniya i Vzryva) 2 (2): 99-106. ISSN 0010-5082. doi:10.1007/BF00749237.
- Tate, A. (1 de noviembre de 1967). «A Theory for the Deceleration of Long Rods After Impact». Journal of the Mechanics and Physics of Solids 15 (6): 387-399. doi:10.1016/0022-5096(67)90010-5. Archivado desde el original el 26 de marzo de 2012. Consultado el 23 de junio de 2011.
- Bernard, Robert S. (1978). Depth and Motion Prediction for Earth Penetrators (Report). ADA056701. Vicksburg, MS: Army Engineer Waterways Experiment Station Vicksburg. Archivado desde el original el 8 de abril de 2013. Consultado el 16 de julio de 2012.
- Walters, William P.; Segletes, Steven B. (1991). «An Exact Solution of the Long Rod Penetration Equations». International Journal of Impact Engineering 11 (2): 225-231. doi:10.1016/0734-743X(91)90008-4.
- Segletes, Steven B.; Walters, William P. (2002). Efficient Solution of the Long-Rod Penetration Equations of Alekseevskii-Tate (Report). ARL-TR-2855. Aberdeen, MD: Army Research Lab Aberdeen Proving Ground MD. Archivado desde el original el 23 de marzo de 2012. Consultado el 16 de julio de 2012.
- Segletes, Steven B.; Walters, William P. (2003). «Extensions to the Exact Solution of the Long-Rod Penetration/Erosion Equations». International Journal of Impact Engineering 28 (4): 363-376. doi:10.1016/S0734-743X(02)00071-4. Consultado el 23 de junio de 2011.
Enlaces externos
- Impact Earth Impact Effects Program Archivado el 5 de mayo de 2010 en Wayback Machine.