Centro radical

Centro radical de tres circunferencias es el punto que tiene igual potencia respecto de las tres circunferencias. Para determinarlo se halla la intersección del eje radical de una pareja de circunferencias con el eje radical de otro par de circunferencias.

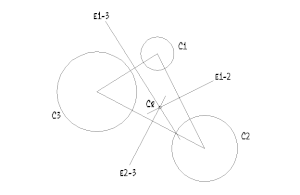
Representación gráfica del Centro radical.

El tercer eje radical de la tercera pareja pasará por la intersección hallada anteriormente (propiedad transitiva), ya que si P(C) es la potencia de un punto P respecto de una circunferencia C, se verifica que:

Si P(C1) = P(C2) y P(C2) = P(C3) => P(C1) = P(C3)

Las tangentes a las tres circunferencias desde el centro radical tienen la misma longitud.