Ordenamiento de burbuja bidireccional
El ordenamiento de burbuja bidireccional (cocktail sort en inglés) es un algoritmo de ordenamiento que surge como una mejora del algoritmo ordenamiento de burbuja.
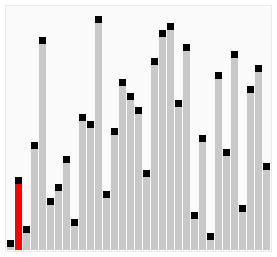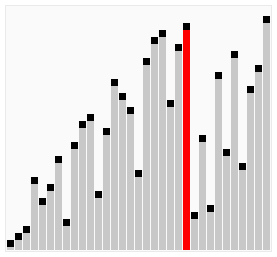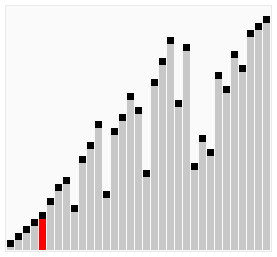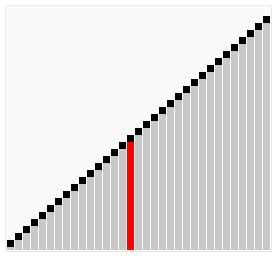
La manera de trabajar de este algoritmo es ir ordenando al mismo tiempo por los dos extremos del vector. De manera que tras la primera iteración, tanto el menor como el mayor elemento estarán en sus posiciones finales. De esta manera se reduce el número de comparaciones aunque la complejidad del algoritmo sigue siendo O(n²).
Hacemos un recorrido ascendente (del primer elemento al último), cogemos el primer elemento y lo comparamos con el siguiente, si el siguiente es menor lo pasamos al puesto anterior, de esta forma al final de la lista nos queda el mayor. Una vez terminada la serie ascendente, hacemos un recorrido descendente (del último elemento al primero) pero esta vez nos quedamos con los menores a los que vamos adelantando posiciones en vez de retrasarlas como hicimos en la serie ascendente. Repetimos las series alternativamente pero reduciendo el ámbito en sus extremos pues ya tendremos allí los valores más bajos y más altos de la lista, hasta que no queden elementos en la serie; en el pseudocódigo de ejemplo: Hasta (izq > der).
A continuación se muestra el pseudo-código del algoritmo:
Procedimiento Ordenacion_Sacudida (v:vector, tam:entero)
Variables
i, j, izq, der, último: tipoposicion;
aux: tipoelemento;
Inicio
//Límites superior e inferior de elementos ordenados
izq <- 2
der <- tam
último <- tam
Repetir
//Burbuja hacia la izquierda}
//Los valores menores van a la izquierda
//der va disminuyendo en 1 hasta llegar a izq
Para i <- der hasta izq hacer
Si v(i-1) > v(i) entonces
aux <- v(i)
v(i) <- v(i-1)
v(i-1) <- aux
último <- i
Fin_si
Fin_para
izq <- último+1
//Burbuja hacia la derecha
//Los valores mayores van a la derecha
Para j <- izq hasta der hacer
Si v(j-1) > v(j) entonces
aux <- v(j)
v(j) <- v(j-1)
v(j-1) <- aux
último <- j
Fin_si
Fin_para
der <- último-1
Hasta (izq > der)
Fin
Enlaces externos
- Distintas implementaciones del algoritmo en Wikibooks (inglés)
- Distintas implementaciones del algoritmo en RosettaCode.org (inglés)