Complejo simplicial
En la matemática, un complejo simplicial es un tipo particular de espacio topológico construido mediante el pegado de puntos, segmentos de línea, triángulos, tetraedros y demás análogos de dimensiones superiores. Este concepto no debe ser confundido con la noción abstracta de conjunto simplicial que surge en la moderna teoría simplicial homotópica
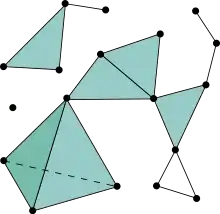
Ejemplo
Sean con que están en posición general, la clausura convexa del conjunto se llama k-símplice de y se denota . Se prueba sin dificultad que:
con y para todas las i.
Los de la representación anterior se llaman coordenadas baricéntricas del punto . Si tomamos , se dice que el r-símplice es una cara de .
Observe que un 0-símplice es un punto, un 1-símplice es un segmento, un 2-símplice es un triángulo y un 3-símplice es un tetraedro.
Caracterización
Un complejo simplicial (finito) es un conjunto finito de - símplices de que cumple las dos condiciones siguientes:
- Si un símplice pertenece a , entonces todas sus caras pertenecen a .
- Si dos símplices de se cortan, su intersección es una cara común.
Referencias
- Weisstein, Eric W. «Complejo simplicial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Hazewinkel, Michiel, ed. (2001), «Complejo simplicial», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.