Conjugado isogonal

En geometría, el conjugado isogonal de un punto ${\displaystyle P}$, respecto de un triángulo ${\displaystyle ABC}$ se construye reflejando las rectas que unen ${\displaystyle P}$ con cada uno de los vértices del triángulo en torno a las bisectrices de ${\displaystyle {\widehat {A}}}$, ${\displaystyle {\widehat {B}}}$ y ${\displaystyle {\widehat {C}}}$ respectivamente. Estas tres rectas reflejadas concurren en el punto conjugado isogonal de ${\displaystyle P}$. Esta definición es válida solamente para los puntos del plano que no se hallen sobre los lados del triángulo ${\displaystyle ABC}$.

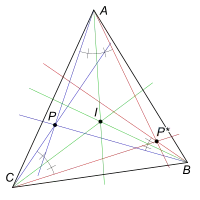
Conjugado Isogonal de P.

El conjugado isogonal de un punto ${\displaystyle P}$ a veces se denota con ${\displaystyle P^{*}}$. El conjugado isogonal de ${\displaystyle P^{*}}$ es ${\displaystyle P}$.