Cuadrilátero armónico

En geometría euclídea, un cuadrilátero armónico o cuadrángulo armónico,[1] es un cuadrilátero que puede inscribirse en una circunferencia (cuadrilátero cíclico) en el que los productos de las longitudes de los lados opuestos son iguales. Tiene varias propiedades importantes.

Cuadrilátero armónico cíclico de lados AB=8; BC=4 ; CD=10; y DA=20. El radio de la circunferencia circunscrita es de aproximadamente 13,855

Propiedades

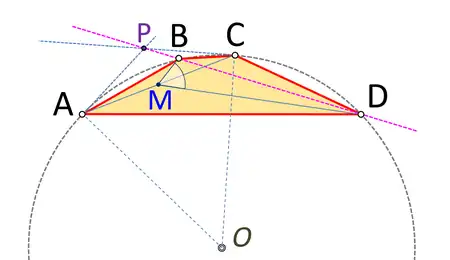
Sea $ABCD$ un cuadrilátero armónico y $M$ el punto medio de la diagonal $AC$ . Entonces:

Las tangentes a la circunferencia circunscrita en los puntos $A$ y $C$ y la línea recta $BD$ se cruzan en un mismo punto o son paralelas entre sí.
Los ángulos $∠BMC$ y $∠DMC$ son iguales.
Las bisectrices de los ángulos de $B$ y $D$ se cruzan en la diagonal $AC$ .
Una diagonal $BD$ del cuadrilátero es una simediana de los ángulos en $B$ y $D$ en los triángulos ∆ $ABC$ y ∆ $ADC$ .

Cuadriláteros armónicos diametrales

Es posible construir cuadriláteros armónicos, de forma que el mayor de los cuatro lados coincida con un diámetro de la circunferencia circunscrita. A continuación se ilustran el caso general y dos casos sencillos:

Caso general

Dado un vétice no diametral, para calcular las coordenadas del segundo vértice no diametral, es necesario efectuar los cálculos siguientes:

Dada una circunferencia de radio 1, se sitúa el lado largo del cuadrilátero armónico sobre el diámetro horizontal. Para calcular los otros dos vértices que definen el cuadrilátero armónico, se definen los parámetros siguientes: $\beta$ : ángulo que fija el primer vértice $k_{x},k_{y}$ : coordenadas del primer vértice ( $k_{x}=\cos \beta$ y $k_{y}=\sin \beta$ ) $L$ : longitud del primer lado $\alpha$ : ángulo para calcular el segundo vértice $(P)$ $c,s$ : coordenadas del segundo vértice $(P)$ ( $c=\cos \alpha$ y $s=\sin \alpha$ ) $L_{1}$ : longitud del segundo lado $L_{2}$ : longitud del tercer lado La condición de que se trate de un cuadrilátero armónico, es que coincida el producto de las longitudes de los lados opuestos. Teniendo en cuenta que el lado que coincide con el diámetro de la circunferencia mide 2: $LL_{2}=2L_{1}$ Expresando estas longitudes en función de los parámetros anteriores, se tiene que: $L={\sqrt {(1-k_{x})^{2}+k_{y}\,^{2}}}$ ; $L_{1}={\sqrt {(c+k_{x})^{2}+(s-k_{y})^{2}}}$ ; $L_{2}={\sqrt {(1-c)^{2}+s^{2}}}$	Sustituyendo en la primera ecuación del producto de las longitudes de los lados opuestos, y elevando ambos términos al cuadrado para eliminar las raíces: $(LL_{2})^{2}=(2L_{1})^{2}$ $(1+k_{x}\,^{2}-2k_{x}+k_{y}\,^{2})(1+c^{2}-2c+s^{2})=4(c^{2}+k_{x}\;^{2}+2ck_{x}+s^{2}+k_{y}\,^{2}-2sk_{y})$ y teniendo en cuenta que $c^{2}+s^{2}=1$ y que $k_{x}\;^{2}+k_{y}\;^{2}=1$ , se opera, y se obtiene que: $2sk_{y}=2{\sqrt {(1-c^{2})}}k_{y}=(k_{x}+1)c+(k_{x}+1)=(k_{x}+1)(c+1)$ Elevando al cuadrado: $4k_{y}\;^{2}(1-c^{2})=(k_{x}+1)^{2}(c+1)^{2}$ $c^{2}((k_{x}+1)^{2}+4k_{y}\,^{2})+c(2(k_{x}+1)^{2})+((k_{x}+1)^{2}-4k_{y}\,^{2})=0$ Esta es una ecuación de segundo grado en $c$ , con los coeficientes $A=(k_{x}+1)^{2}+4k_{y}\,^{2}$ // $B=2(k_{x}+1)^{2}$ // $C=(k_{x}+1)^{2}-4k_{y}\,^{2}$ que se resuelve mediante la fórmula: $c={\frac {-B+{\sqrt {B^{2}-4AC}}}{2A}}$ (en este caso, la solución correcta es con el signo + de la raíz) Una vez calculado $c$ , se tiene que $\alpha ={\text{Arcocos }}c$ , y que el punto buscado tiene las coordenadas del segundo vértice $(P)$ , que son: $P=(\sin \alpha ,\cos \alpha )$

En la tabla siguiente se incluye el resultado obtenido a partir de fijar el primer vértice no diametral mediante intervalos de 5 en cinco grados del ángulo $\beta$ :

Coordenadas y dimensiones de los cuadriláteros armónicos diametrales:
BETA	K_x (cos)	K_y(sin)	L (cuerda)	ALFA	x	y	L₁	L₂	ÁREA	PERÍMETRO	Vértice X	Vértice Y
5	0,996195	0,087156	0,087239	170,018966	-0,984865	0,173322	0,086908	1,992418	0,130239	4,166565	-0,992404	0,17398
10	0,984808	0,173648	0,174311	160,15003	-0,940585	0,339558	0,171703	1,970069	0,256603	4,316083	-0,969845	0,344678
15	0,965926	0,258819	0,261052	150,49711	-0,870331	0,492467	0,252448	1,934079	0,375643	4,447579	-0,932993	0,508967
20	0,939693	0,34202	0,347296	141,1492	-0,778782	0,627295	0,327527	1,886151	0,484657	4,560974	-0,882916	0,664018
25	0,906308	0,422618	0,432879	132,176026	-0,671411	0,741086	0,395725	1,828338	0,581852	4,656942	-0,821001	0,807412
30	0,866025	0,5	0,517638	123,626429	-0,553776	0,832666	0,456253	1,762825	0,666333	4,736716	-0,748873	0,937218
35	0,819152	0,573576	0,601412	115,529137	-0,43097	0,902366	0,508712	1,691727	0,737971	4,801851	-0,668298	1,052025
40	0,766044	0,642788	0,68404	107,895223	-0,307277	0,95162	0,553032	1,616958	0,797204	4,854031	-0,581092	1,150941
45	0,707107	0,707107	0,765367	100,721456	-0,186035	0,982543	0,589391	1,540152	0,844825	4,89491	-0,489042	1,233563
50	0,642788	0,766044	0,845237	93,993857	-0,06965	0,997572	0,618136	1,462634	0,881808	4,926007	-0,393839	1,299916
55	0,573576	0,819152	0,923497	87,690998	0,040289	0,999188	0,639721	1,385432	0,90917	4,948651	-0,297034	1,350386
60	0,5	0,866025	1	81,786789	0,142857	0,989743	0,654654	1,309307	0,927884	4,963961	-0,2	1,385641
65	0,422618	0,906308	1,074599	76,25268	0,23764	0,971353	0,663455	1,234795	0,93883	4,972849	-0,103925	1,406556
70	0,34202	0,939693	1,147153	71,05929	0,32459	0,945855	0,666638	1,162248	0,942774	4,976039	-0,009805	1,414146
75	0,258819	0,965926	1,217523	66,177552	0,403904	0,914801	0,664692	1,091876	0,940364	4,97409	0,08155	1,409503
80	0,173648	0,984808	1,285575	61,579466	0,475939	0,879478	0,658072	1,023778	0,932143	4,967425	0,169496	1,393751
85	0,087156	0,996195	1,35118	57,238555	0,541142	0,840931	0,647198	0,957974	0,918563	4,956353	0,253544	1,368003
90	0	1	1,414214	53,130102	0,6	0,8	0,632456	0,894427	0,9	4,941096	0,333333	1,333333
95	-0,087156	0,996195	1,474555	49,231243	0,653008	0,757351	0,614194	0,833057	0,876773	4,921806	0,408618	1,290761
100	-0,173648	0,984808	1,532089	45,520953	0,700648	0,713507	0,592734	0,773759	0,849157	4,898582	0,479242	1,241231
105	-0,258819	0,965926	1,586707	41,97997	0,743379	0,668871	0,568366	0,71641	0,817398	4,871482	0,545123	1,185615
110	-0,34202	0,939693	1,638304	38,590685	0,781622	0,623753	0,541357	0,660875	0,781723	4,840537	0,606238	1,1247
115	-0,422618	0,906308	1,686783	35,337009	0,815764	0,578385	0,511954	0,607019	0,742346	4,805756	0,662608	1,059198
120	-0,5	0,866025	1,732051	32,204228	0,846154	0,532939	0,480384	0,5547	0,699482	4,767135	0,714286	0,989743
125	-0,573576	0,819152	1,774022	29,178863	0,873102	0,487538	0,44686	0,503782	0,653345	4,724663	0,761346	0,916899
130	-0,642788	0,766044	1,812616	26,248536	0,896884	0,442266	0,411579	0,454128	0,604155	4,678323	0,80388	0,841163
135	-0,707107	0,707107	1,847759	23,401839	0,917742	0,397177	0,374731	0,405606	0,552142	4,628096	0,841983	0,762974
140	-0,766044	0,642788	1,879385	20,62821	0,935886	0,352302	0,336493	0,358089	0,497545	4,573968	0,875755	0,682719
145	-0,819152	0,573576	1,907434	17,917822	0,951499	0,307653	0,297037	0,311452	0,440615	4,515923	0,905294	0,600737
150	-0,866025	0,5	1,931852	15,26148	0,964735	0,263225	0,256527	0,265576	0,381612	4,453955	0,930691	0,517327
155	-0,906308	0,422618	1,952592	12,650524	0,975724	0,219004	0,215122	0,220345	0,320811	4,388059	0,95203	0,432755
160	-0,939693	0,34202	1,969616	10,076738	0,984574	0,174967	0,172977	0,175646	0,258494	4,318238	0,969385	0,347256
165	-0,965926	0,258819	1,98289	7,532266	0,991371	0,131084	0,130244	0,131368	0,194952	4,244502	0,982817	0,261043
170	-0,984808	0,173648	1,992389	5,009537	0,99618	0,087322	0,087072	0,087405	0,130485	4,166867	0,992375	0,17431
175	-0,996195	0,087156	1,998096	2,50119	0,999047	0,04364	0,043609	0,043651	0,065398	4,085356	0,998096	0,087239
70,52877937	0,333333	0,942809	1,154701	70,528779	0,333333	0,942809	0,666667	1,154701	0,942809	4,976068	0	1,414214

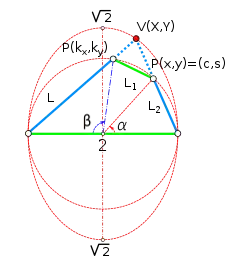
Construcción general de un cuadrilátero armónico diametral

En esta tabla, además de las coordenadas de los puntos del cuadrilátero, se han incluido sus áreas y perímetros. Se puede comprobar que tanto el área como el perímetro máximos corresponden a la solución simétrica (incluida en la última fila de la tabla).

También aparecen las coordenadas de los vértices (X, Y), resultantes de la intersección de prolongar los dos lados adyacentes al diámetro. Se comprueba que todos estos vértices se sitúan sobre una elipse, cuyo centro coincide con el de la circunferencia, el semieje menor mide 1 y coincide con uno de los radios del diámetro que forma parte de los cuadriláteros, y cuyo semieje mayor vale ${\sqrt {2}}=1,414214...$ .

En consecuencia:

Al trazar desde un punto cualquiera de la elipse dos segmentos hasta los extremos del diámetro base, al cortarse con la circunferencia se generan los otros dos vértices de un cuadrilátero armónico diametral

Cuadrilátero armónico diametral ortogonal

Cuadrilátero armónico diametral ortogonal: el lado inferior es un diámetro, uno de los lados azules termina en el extremo de un radio perpendicular al lado diámetral, y el producto de las longitudes de los lados verdes es igual a la de los lados azules

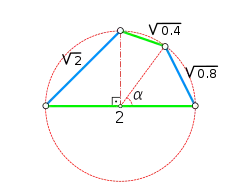
Partiendo de una circunferencia de radio 1, se tiene que la longitud del lado más largo del cuadrilátero coincide con la de un diámetro, y por lo tanto vale 2. El segundo lado conecta uno de los extremos del lado anterior con el extremo de un radio perpendicular al diámetro en cuestión. Las dimensiones de los dos lados restantes del cuadrilátero se calculan determinando el ángulo $\alpha$ que haga que se igualen los productos de las longitudes opuestas, es decir:

{\sqrt {2}}*{\sqrt {(1-\cos \alpha )^{2}+\sin \alpha ^{2}}}=2*{\sqrt {\cos \alpha ^{2}+(1-\sin \alpha )^{2}}}

elevando al cuadrado ambos lados de la ecuación y operando la expresión resultante se llega a:

2(1+\cos \alpha ^{2}-2\cos \alpha +\sin \alpha ^{2})=4(\cos \alpha ^{2}+1+\sin \alpha ^{2}-2\sin \alpha )

de donde se obtiene que

\cos \alpha =1-2(1-\sin \alpha )=2\sin \alpha -1

elevando ambos términos al cuadrado, se tiene que

\cos \alpha ^{2}=(2\sin \alpha -1)^{2}

1-\sin \alpha ^{2}=4\sin \alpha ^{2}-4\sin \alpha +1

5\sin \alpha ^{2}-4\sin \alpha =0

; y entonces

5\sin \alpha -4=0

de donde

\sin \alpha =4/5=0.8

, y

\alpha ={\text{Arcosin}}(0.8)=53.13010235...{\text{°}}

A partir de este ángulo, se tiene que $\cos \alpha =0.6$ , y entonces:

${\text{Lado opuesto al diámetro}}={\sqrt {\cos \alpha ^{2}+(1-\sin \alpha )^{2}}}={\sqrt {0.6^{2}+0.2^{2}}}={\sqrt {0.4}}=0.632455532...$
${\text{Cuarto lado}}={\sqrt {(1-\cos \alpha )^{2}+\sin \alpha ^{2}}}={\sqrt {0.8^{2}+0.4^{2}}}={\sqrt {0.8}}=0.89442719...$

Cuadrilátero armónico diametral simétrico

Cuadrilátero armónico diametral simétrico: el lado inferior es un diámetro, los dos lados azules son de igual longitud, y el producto de las longitudes de los lados verdes es igual a la de los lados azules

Partiendo de una circunferencia de radio 1, se tiene que la longitud del lado más largo del cuadrilátero coincide con la de un diámetro, y por lo tanto vale 2. Las dimensiones de los otros tres lados del cuadrilátero se calculan determinando el ángulo $\alpha$ que haga que se igualen los productos de las longitudes opuestas, es decir:

2*2\cos \alpha ={\Big (}{\sqrt {(1-\cos \alpha )^{2}+\sin \alpha ^{2}}}{\Big )}^{2}

operando esta expresión se llega a:

4\cos \alpha =2-2\cos \alpha

de donde se obtiene que

\cos \alpha =1/3

, y

\alpha ={\text{Arcocos}}(1/3)=70.52877937...{\text{°}}

A partir de este ángulo, se tiene que:

${\text{Lado superior}}=2\cos \alpha =2*1/3=0.6666666$
${\text{Lados laterales}}={\sqrt {(1-\cos \alpha )^{2}+\sin \alpha ^{2}}}={\sqrt {0.444444+0.8888888}}=2{\frac {\sqrt {3}}{3}}=1.154700538...$

Referencias

Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover, p. 100, ISBN 978-0-486-46237-0.

Lecturas relacionadas

Gallatly, W. "The Harmonic Quadrilateral." §124 in The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, pp. 90 and 92, 1913.

Datos: Q12094381

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover, p. 100, ISBN 978-0-486-46237-0.