Curva cuártica
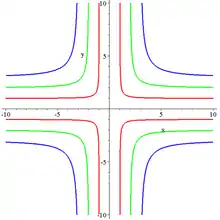
Una curva plana cuártica o curva cuártica es una curva plana de cuarto grado. Se puede definir mediante una ecuación cuártica:
 |  | |||
|---|---|---|---|---|
 |  | |||
Esta ecuación tiene quince constantes. Sin embargo, si se multiplica por cualquier constante no nula, la curva permanece invariante. Por tanto, el espacio de las curvas cuárticas se puede identificar con el espacio real proyectivo . También se sigue de ello el que, dados catorce puntos distintos en posición general, exista exactamente una curva cuártica que pasa por todos ellos, ya que una cuártica tiene 14 grados de libertad.
Una curva cuártica puede tener un máximo de:
- Cuatro componentes conexas;
- Veintiocho bitangentes;
- Tres puntos dobles ordinarios.
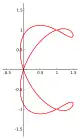
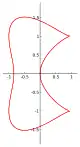
Ejemplos
- Curva deltoide
- Cuártica de Klein
- Lemniscata de Gerono
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.