Dispersión refractiva

Animación esquemática de un haz continuo de luz dispersado por un prisma. El haz blanco representa muchas longitudes de onda de luz visible, de las cuales se muestran 7, al atravesar un vacío a la misma velocidad c. El prisma hace que la luz se ralentice, curvando su camino por el proceso de refracción. Este efecto es más pronunciado en las longitudes de onda más cortas (como el extremo violeta) que en las longitudes de onda más largas (como el extremo rojo), dispersando así los componentes. Al salir del prisma, cada componente vuelve a la misma velocidad original y se refracta nuevamente.

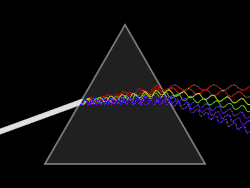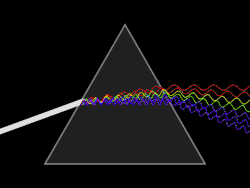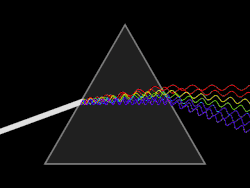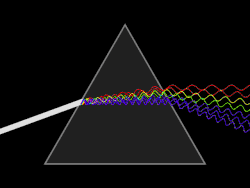
La descomposición de la luz blanca en los diferentes colores que la componen (data del siglo XVIII) debido al físico, astrónomo y matemático Isaac Newton. La luz blanca se descompone en estos colores principales:

• Rojo (el color que experimenta la menor desviación).
• Anaranjado.
• Amarillo.
• Verde.
• Azul.
• Añil.
• Violeta (el color que experimenta la mayor desviación).

Esto demuestra que la luz blanca está constituida por la superposición de todos estos colores. Cada uno de los cuales experimenta una desviación distinta ya que el índice de refracción de, por ejemplo, el vidrio es diferente para cada uno de los colores.

Si la luz de un color específico, proveniente del espectro de la luz blanca, atravesara un prisma, esta no se descompondría en otros colores ya que cada color que compone el espectro es un color puro o monocromático.

La dispersión cromática suele referirse a la dispersión del material a granel, es decir, al cambio del índice de refracción con la frecuencia óptica. Sin embargo, en una guía de ondas también existe el fenómeno de dispersión en guía de ondas, en cuyo caso la velocidad de fase de una onda en una estructura depende de su frecuencia simplemente debido a la geometría de la estructura. En términos más generales, la dispersión de la guía de onda puede ocurrir para las ondas que se propagan a través de cualquier estructura no homogénea (por ejemplo, un cristal fotónico), independientemente de que las ondas estén confinadas en alguna región.{En una guía de ondas, ambos tipos de dispersión estarán generalmente presentes, aunque no son estrictamente aditivos. Por ejemplo, en la fibra óptica la dispersión del material y de la guía de onda pueden anularse mutuamente de forma efectiva para producir una longitud de onda de dispersión cero, importante para la comunicación por fibra óptica rápida.

La variación del índice de refracción vs. la longitud de onda en vacío para varios vidrios. Las longitudes de onda de la luz visible están resaltadas en gris.

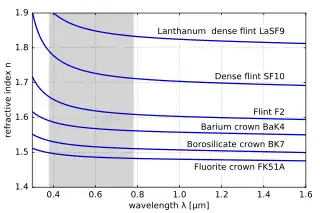
La dispersión del material puede ser un efecto deseable o indeseable en las aplicaciones ópticas. La dispersión de la luz por prismas de vidrio se utiliza para construir espectrómetros y espectroradiómetros. Sin embargo, en las lentes, la dispersión provoca aberración cromática, un efecto no deseado que puede degradar las imágenes en microscopios, telescopios y objetivos fotográficos.

La velocidad de fase, v, de una onda es un dado medio uniforme se expresa como

${\displaystyle v={\frac {c}{n}}}$

donde c es la velocidad de la luz en el vacío y n es el índice de refracción del medio.

En general, el índice de refracción es una función de la frecuencia f de la luz, o sea n = n(f), o de forma alternativa, con respecto a la longitud de onda de la onda n = n(λ). La dependencia de la longitud de onda del índice de refracción del material es por lo general cuantificada por su número de Abbe o sus coeficientes en una fórmula empírica tales como las ecuaciones de Cauchy o Sellmeier.

Debido a las relaciones de Kramers-Kronig, la dependencia de la longitud de onda de la parte real del índice de refracción se encuentra relacionada con la absorción del material, descripta por la componente imaginaria del índice de refracción (también denominado el coeficiente de extinción). En particular, para el caso de materiales no-magnéticos (μ = μ₀), la susceptibilidad χ que aparece en las relaciones de Kramers–Kronig es la susceptibilidad eléctrica χ_e = n² − 1.

La consecuencia comúnmente observada de la dispersión en óptica es la separación de la luz blanca en el espectro de colores mediante un prisma. A partir de la ley de Snell se observa que el ángulo de refracción de la luz en un prisma depende del índice de refracción del material del prisma. Como ese índice de refracción varía con la longitud de onda, se deduce que el ángulo con el que se refracta la luz también variará con la longitud de onda, provocando una separación angular de los colores conocida como dispersión angular.

Para la luz visible, los índices de refracción n de la mayoría de los materiales transparentes (por ejemplo, el aire, los vidrios) disminuyen al aumentar la longitud de onda λ:

${\displaystyle 1<n(\lambda _{\rm {red}})<n(\lambda _{\rm {yellow}})<n(\lambda _{\rm {blue}})\ ,}$

o alternativamente:

${\displaystyle {\frac {dn}{d\lambda }}<0.}$

En este caso, se dice que el medio tiene una dispersión normal. Mientras que, si el índice aumenta con el incremento de la longitud de onda (lo que suele ocurrir en el ultravioleta[1]), se dice que el medio tiene una dispersión anómala.

En la interfaz de dicho material con el aire o el vacío (índice de ~1), la ley de Snell predice que la luz que incide en un ángulo θ con respecto a la normal se refractará en un ángulo arcsin(sin θ/n). Por lo tanto, la luz azul, con un índice de refracción más alto, se refractará más fuertemente que la luz roja, dando como resultado el conocido patrón del arco iris.

Evolución temporal de un pulso corto en un hipotético medio dispersivo (k=w^2) que muestra que los componentes de mayor longitud de onda viajan más rápido que los de menor longitud de onda (GVD positiva), lo que da lugar a un chirrido y a un ensanchamiento del pulso.

Más allá de la simple descripción de un cambio en la velocidad de fase con respecto a la longitud de onda, una consecuencia más grave de la dispersión en muchas aplicaciones se denomina dispersión de la velocidad de grupo (GVD). Mientras que la velocidad de fase v se define como v = c/n, esto describe sólo un componente de frecuencia. Cuando se combinan diferentes componentes de frecuencia, como cuando se considera una señal o un pulso, uno suele estar más interesado en la velocidad de grupo que describe la velocidad a la que se propaga un pulso o información superpuesta a una onda (modulación). En la animación adjunta, se puede ver que la propia onda (naranja-marrón) viaja a una velocidad de fase que es mucho más rápida que la velocidad de la envoltura (negro) que corresponde a la velocidad de grupo. Este pulso podría ser una señal de comunicaciones, por ejemplo, y su información sólo viaja a la velocidad de grupo aunque esté formada por frentes de onda que avanzan a una velocidad mayor (la velocidad de fase).

Es posible calcular la velocidad de grupo a partir de la curva del índice de refracción n(ω) o más directamente a partir del número de onda k = ωn/c donde ω es la frecuencia en radianes ω=2πf. Mientras que una expresión de la velocidad de fase es v_p=ω/k, la velocidad de grupo se puede expresar utilizando la derivada: v_g=dω/dk. O en función de la velocidad de fase v_p,

${\displaystyle {v_{g}}={\frac {v_{p}}{1-{\frac {\omega }{v_{p}}}{\frac {dv_{p}}{d\omega }}}}.}$

Cuando hay dispersión, la velocidad de grupo no sólo no es igual a la velocidad de fase, sino que generalmente varía con la longitud de onda. Esto se conoce como dispersión de la velocidad de grupo y hace que un pulso corto de luz se ensanche, ya que los diferentes componentes de frecuencia dentro del pulso viajan a diferentes velocidades. La dispersión de la velocidad de grupo se cuantifica como la derivada del recíproco de la velocidad de grupo con respecto a la frecuencia del radián, lo que resulta en la dispersión de la velocidad de grupo = d²k/dω².

Si un pulso de luz se propaga a través de un material con dispersión de velocidad de grupo positiva, los componentes de menor longitud de onda viajan más lentamente que los componentes de mayor longitud de onda. Por lo tanto, el pulso se convierte en un "chirrido positivo", o "chirrido ascendente", aumentando la frecuencia con el tiempo. Por otro lado, si un pulso viaja a través de un material con dispersión de velocidad de grupo negativa, los componentes de longitud de onda más cortos viajan más rápido que los más largos, y el pulso se vuelve negativamente chirpado, o down-chirped, disminuyendo en frecuencia con el tiempo.

Un ejemplo cotidiano de señal con chirrido negativo en el ámbito acústico es el de un tren que se aproxima y choca con las deformaciones de una vía soldada. El sonido provocado por el propio tren es impulsivo y viaja mucho más rápido en las vías metálicas que en el aire, por lo que el tren se oye mucho antes de llegar. Sin embargo, desde lejos no se oye como si provocara impulsos, sino que da lugar a un distintivo chirrido descendente, en medio de la reverberación causada por la complejidad de los modos vibratorios de la vía. La dispersión de la velocidad del grupo se percibe en que el volumen de los sonidos permanece audible durante un tiempo sorprendentemente largo, hasta varios segundos.

El parámetro de dispersión de la velocidad de grupo:

${\displaystyle D={\frac {1}{c}}\,{\frac {dn}{d\lambda }}.}$

a menudo se utiliza para cuantificar GVD, que es proporcional a D a través de un factor negativo:

${\displaystyle D=-{\frac {2\pi c}{\lambda ^{2}}}\,{\frac {d^{2}k}{d\omega ^{2}}}.}$

Según algunos autores se dice que un medio tiene una dispersión normal/dispersión anormal para determinadas longitudes de onda en vacío λ₀ si la segunda derivada del índice de refracción calculada en λ₀ es positiva/negativa o, de manera equivalente, si D(λ₀) es negativo/positivo.[2] Esta definición se refiere a la dispersión de la velocidad de grupo y no debe confundirse con la dada en la sección anterior. Las dos definiciones no coinciden en general, por lo que el lector debe entender el contexto.

La descripción de la dispersión cromática de forma perturbativa mediante coeficientes de Taylor es ventajosa para los problemas de optimización en los que es necesario equilibrar la dispersión de varios sistemas diferentes. Por ejemplo, en los amplificadores láser de pulsos chirp, los pulsos se estiran primero en el tiempo mediante un estirador para evitar daños ópticos. Después, en el proceso de amplificación, los pulsos acumulan inevitablemente fase lineal y no lineal al pasar por los materiales esto desenfoca el punto radial del espejo por eso se ve así con esos colores. Y por último, los pulsos se comprimen en varios tipos de compresores. Para cancelar cualquier orden residual superior en la fase acumulada, normalmente se miden y equilibran los órdenes individuales. Sin embargo, para los sistemas uniformes, esta descripción perturbadora no suele ser necesaria (por ejemplo, la propagación en guías de onda). Los órdenes de dispersión se han generalizado de una manera computacionalmente amigable, en forma de transformadas de tipo Lah-Laguerre.[3][4]

Los órdenes de dispersión se definen por la expansión de Taylor de la fase o del vector de onda.

${\displaystyle {\begin{array}{c}\varphi \mathrm {(} \omega \mathrm {)} =\varphi \left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial \varphi }{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}\varphi }{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}\varphi }{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

${\displaystyle {\begin{array}{c}k\mathrm {(} \omega \mathrm {)} =k\left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial k}{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}k}{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}k}{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

Las relaciones de dispersión para el wavector ${\displaystyle k\mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}n\mathrm {(} \omega \mathrm {)} }$ y la fase ${\displaystyle \varphi \mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}{\it {OP}}\mathrm {(} \omega \mathrm {)} }$ puede expresarse como:

${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}k\mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}n\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}n\mathrm {(} \omega \mathrm {)} \right)\ \end{array}}}$, ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}\varphi \mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} \right)\end{array}}(1)}$

Las derivadas de cualquier función diferenciable ${\displaystyle f\mathrm {(} \omega \mathrm {|} \lambda \mathrm {)} }$ en la longitud de onda o el espacio de la frecuencia se especifica a través de una transformada de Lah como:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}(2)}$

Los elementos de la matriz de la transformación son los coeficientes de Lah: ${\displaystyle {\mathcal {A}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {1)!} }{\mathrm {(} m\mathrm {-} \mathrm {1)!} }}}$

Escrita para la GDD la expresión anterior establece que una constante con longitud de onda GGD, tendrá cero órdenes superiores. Los órdenes superiores evaluados a partir del GDD son: ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}GDD\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}GDD\mathrm {(} \lambda \mathrm {)} }\end{array}}}$

Sustituyendo la ecuación (2) expresada para el índice de refracción ${\displaystyle n}$ o el recorrido óptico ${\displaystyle OP}$ en la ecuación (1) se obtienen expresiones de forma cerrada para los órdenes de dispersión. En general la dispersión de orden ${\displaystyle p^{th}}$ POD es una transformada de tipo Laguerre de orden negativo dos:

${\displaystyle POD={\frac {d^{p}\varphi (\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}OP(\lambda )}{d\lambda ^{m}}}}$ ${\displaystyle ,}$ ${\displaystyle POD={\frac {d^{p}k(\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}n(\lambda )}{d\lambda ^{m}}}}$

Los elementos de la matriz de las transformaciones son los coeficientes de Laguerre sin signo de orden menos 2, y están dados como: ${\displaystyle {\mathcal {B}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {2)!} }{\mathrm {(} m\mathrm {-} \mathrm {2)!} }}}$

Los diez primeros órdenes de dispersión, escritos explícitamente para el vector de onda, son:

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GD}}}={\frac {\partial }{\partial \omega }}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \omega \mathrm {)} +\omega {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \lambda \mathrm {)} -\lambda {\frac {\partial n\mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\right)=v_{gr}^{\mathrm {-} \mathrm {1} }\end{array}}}$

El índice de refracción de grupo ${\displaystyle n_{g}}$ se define como: ${\displaystyle n_{g}=cv_{gr}^{\mathrm {-} \mathrm {1} }}$.

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GDD}}}={\frac {{\partial }^{2}}{\partial {\omega }^{\mathrm {2} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {2} {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}+\omega {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}\right)={\frac {\mathrm {1} }{c}}\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)\left({\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TOD}}}={\frac {{\partial }^{3}}{\partial {\omega }^{\mathrm {3} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {3} {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}+\omega {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }{\Bigl (}\mathrm {3} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FOD}}}={\frac {{\partial }^{4}}{\partial {\omega }^{\mathrm {4} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {4} {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}+\omega {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }{\Bigl (}\mathrm {12} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {8} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FiOD}}}={\frac {{\partial }^{5}}{\partial {\omega }^{\mathrm {5} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {5} {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}+\omega {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {60} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {60} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {15} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SiOD}}}={\frac {{\partial }^{6}}{\partial {\omega }^{\mathrm {6} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {6} {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}+\omega {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {360} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {480} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {180} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {24} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+{\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SeOD}}}={\frac {{\partial }^{7}}{\partial {\omega }^{\mathrm {7} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {7} {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {6} }}}+\omega {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {2520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {2100} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {420} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {35} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {EOD}}}={\frac {{\partial }^{8}}{\partial {\omega }^{\mathrm {8} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {8} {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}+\omega {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {20160} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {40320} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {25200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {6720} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {840} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {48} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+{\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {NOD}}}={\frac {{\partial }^{9}}{\partial {\omega }^{\mathrm {9} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {9} {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}+\omega {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {181440} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {423360} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {317520} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {105840} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {17640} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {1512} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {63} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TeOD}}}={\frac {{\partial }^{10}}{\partial {\omega }^{\mathrm {10} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {10} {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}+\omega {\frac {{\partial }^{10}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {1814400} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4838400} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4233600} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{1693440}{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\\+\mathrm {352800} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {40320} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {2520} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {80} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

Explícitamente, escrito para la fase ${\displaystyle \varphi }$, los diez primeros órdenes de dispersión se pueden expresar en función de la longitud de onda utilizando las transformadas de Lah (ecuación (2)) como:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}={-}\left({\frac {\mathrm {2} \pi c}{{\omega }^{\mathrm {2} }}}\right){\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \lambda }}={-}\left({\frac {{\lambda }^{\mathrm {2} }}{\mathrm {2} \pi c}}\right){\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{2}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}={\frac {\partial }{\partial \omega }}\left({\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }\left(\mathrm {2} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+{\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{3}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }\left(\mathrm {6} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {6} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{4}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {24} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {36} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{\mathrm {5} }\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {120} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {240} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {20} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{6}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {720} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1800} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {300} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {30} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}\mathrm {\ +} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{7}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {7} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {5040} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {15120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12600} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {630} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {42} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{8}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {40320} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {141120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {141120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {58800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {11760} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {1176} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {56} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\\+{\lambda }^{\mathrm {8} }{\frac {\partial ^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$ ${\displaystyle {\begin{array}{l}{\frac {{\partial }^{9}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {362880} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1451520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1693440} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {846720} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {211680} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {28224} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {2016} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {72} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {\partial ^{\mathrm {9} }\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{10}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {10} }{\Bigl (}\mathrm {3628800} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {16329600} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {21772800} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {12700800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {3810240} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {635040} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {60480} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {3240} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {90} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

• Dispersión (física)
• Prisma (óptica)

• Hewitt, Paul (2004). «28». Física Conceptual (Novena edición). PEARSON EDUCACIÓN. p. 544. ISBN 970-26-0447-8. |fechaacceso= requiere |url= (ayuda)