Distancia de Damerau-Levenshtein
En la teoría de la información y en la ciencia de computadores, se llama distancia de Damerau-Levenshtein o distancia de edición al número mínimo de operaciones requeridas para transformar una cadena de caracteres en otra. Se entiende por operación, bien una inserción, eliminación, sustitución o transposición de dos caracteres. Lo que la distingue de la distancia de Levenshtein es que esta última cuenta como una sola operación de edición a cualquiera de las tres primeras, pero cuenta la transposición como dos operaciones de edición.
Veamos un ejemplo sencillo, calculemos la distancia Damerau-Levenshtein entre la palabra DAR y la palabra DAS. Observamos que los dos primeros caracteres son iguales, y que simplemente hemos de transformar el tercer caracter, es decir, hemos de hacer una única transformación, que consistirá en sustituir la letra R por la letra S. Puesto que hemos hecho una transformación, la distancia Damerau-Levenshtein entre las palabras DAR y DAS es 1.
Las distancia Damerau-Levenshtein se distingue de la distancia Damerau en que la primera considera que la operación de trasposición es una única operación. Un ejemplo de la operación de trasposición sería la que se daría entre las cadena de texto POTRO y PORTO. La distancia Damerau-Levenshtein entre estas dos palabras es 1 porque hemos hecho una operación para pasar de una a otra, la operación de trasposición.
La distancia Damerau-Levenshtein se emplea, por ejemplo, en motores de búsqueda de cadenas de texto. Uno de los motores de búsqueda más conocidos que emplea esta distancia de edición es Lucene. Lo emplea, por ejemplo, para corregir errores de tecleo: imaginemos que estoy buscando las obras del director de cine "Hitchcock", y lo tecleo de forma incorrecta, tecleo "Hichcock". Este motor de búsqueda, y los motores de búsqueda que se basan en él tales como Solr, nos dan las coincidencias con la palabra tecleada con una distancia de hasta 2, de manera que, pese a tecleáramos mal el nombre del director, aparecerían los resultados correspondientes al nombre correcto del director, dado que entre "Hitchcock" y "Hichcock" la distancia es de 1.
Hemos tomado como ejemplo varios casos sencillos, para cadenas de caracteres más largas y complejas se utiliza una matriz que se va completando de forma algorítmica de acuerdo con una serie de condiciones.
Las condiciones lógicas para rellenar la matriz son las siguientes:
Ejemplo de rellenado de una casilla de la matriz de distancia Damerau-Levensthein
Elaborar una matriz completa es un proceso un tanto laborioso, de manera que nos centraremos en rellenar una casilla concreta de la matriz de distancia Damerau-Levensthein siguiendo las condiciones lógicas para ejemplificar el proceso.
Supongamos que deseamos calcular la distancia entre las cadenas de caracteres (cadena a) HITCHCOCK y (cadena b) HICHCOCK.
Presentaremos a continuación la matriz parcialmente completa y veremos cómo rellenar una de las casillas relevantes.
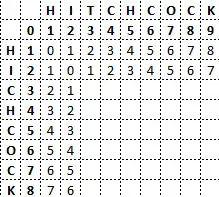
Veamos cómo calcular el valor de la fila(i) = 3,columna(j) = 3.
Su valor Da,b(3,3) es el mínimo de los valores siguientes:
- condición 1. No procede porque i y j son distintos de 0
- condición 2. Valor de Da,b(2,3) + 1 = 1 + 1 = 2
- condición 3. Valor de Da,b(3,2) + 1 = 1 + 1 = 2
- condición 4. Valor de Da,b(2,2) + 1 si a3 diferente de b3 = 0 + 1 = 1
- condición 5. No procede porque a3 es diferente de b2
Por tanto, el valor de la casilla (3,3) es 1.
Es importante fijarse en la condición 3. Dado que a3 y b3 son distintos, su valor es 1. De lo contrario, su valor habría sido 0.
El valor de la distancia Damerau-Levensthein viene dado por la diagonal principal, y ahora pasa a ser 1.
Esta es la matriz actualizada con el valor calculado:
Enlaces externos
- Implementación en C++ de la distancia de Damerau-Levenshtein como UDF para MySQL
- ejemplo de desarrollo completo de una matriz Damerau-Levenshtein
| Control de autoridades |
|
|---|
Datos: Q2657425