Distribución de grado
En el estudio de grafos y redes complejas, el grado de un vértice en una red es el número de conexiones asociadas a un vértice, si se hiciera un recuento en una red del número de nodos por cada grado se tendría una distribución de grado que sería entendido igualmente como la distribución de probabilidad de un grado en la red.[1]
Definición
El grado de un nodo en una red (a veces denominado incorrectamente como conectividad) es el número de conexiones de un vértice o nodo con otros nodos. Si una red es dirigida, esto significa que habrá enlaces que salgan y otros que entren de los nodos y por lo tanto se mencionará que existen grados de salida y de entrada en función de la disposición de los enlaces entrantes y salientes de los nodos.
La distribución de grado en una red se representa habitualmente como P(k) y es definida como la fracción de nodos en la red con un cierto grado k. Es como decir que si la red posee una cantidad de n nodos en total y nk de ellos repartidos en cada grado k, de esta forma se tiene que P(k) = nk/n. La misma información se presenta en forma de una distribución cumulativa de grado que viene a indicar la fracción de nodos con un grado mayor o igual que k.[2]
Tipos
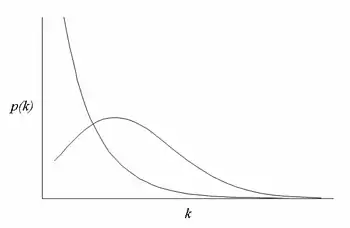
Una de las propiedades más importantes del análisis de la estructura de las redes es quizás la distribución de grado , debido a que proporciona la probabilidad de que un nodo elegido al azar de la red tenga exactamente k conexiones (o vecinos). Se han podido clasificar las redes en función de la distribución de grado en diversas topologías, las más conocidas son:
- Topología de Poisson: Se consideran importantes por ser las que se empezaron a utilizar en el modelo de Erdös-Renyi en la década de los años 50. A veces por esta razón se les denomina redes de tipo Erdös-Renyi. A pesar de ello la representación de redes bajo esta distribución de grado no es realista de las redes que aparecen en la naturaleza.
- Topología Exponencial: Se produce esta topología en las redes evolucionistas en el tiempo siempre que cada nuevo nodo que se añade, posee la misma probabilidad de ser enlazado que el resto. a esta propiedad se le denomina enlace igualitario'.
- Topología Libre de Escala: Los estudios realizados por Barabási acerca de las redes complejas dieron lugar a estudios de redes con este tipo de distribución de grado. Algunas de las redes más comunes de la naturaleza muestran esta distribución, como puede ser internet, las redes sociales, etc.
Bibliografía
- Albert, R.; Barabasi, A.-L. (2002). «Statistical mechanics of complex networks». Reviews of Modern Physics 74: 47-97.
- Dorogovtsev, S.; Mendes, J. F. F. (2002). «Evolution of networks». Advances in Physics 51: 1079-1187.
- Newman, M. E. J. (2003). «The structure and function of complex networks». SIAM Review 45: 167-256. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
Referencias
- "Linked: The New Science of Networks", Albert-László Barabási, Basic Books, 2003, ISBN 0-7382-0667-9
- "Random Networks with Tunable Degree Distribution and Clustering", Erik McCullough Volz, Cornell University, Jan, 2005