Ecuación de Burgers
La ecuación de Burgers o ecuación de Bateman-Burgers es una ecuación diferencial parcial fundamental que ocurre en varias áreas de la matemática aplicada, como la mecánica de fluidos,[1] la acústica no lineal,[2] la dinámica de gases y el flujo de tráfico. La ecuación fue introducida por primera vez por Harry Bateman en 1915[3][4] y luego estudiada por Johannes Martinus Burgers en 1948.[5]
Para un campo dado y coeficiente de difusión o viscosidad cinemática, como en el contexto mecánico original del fluido, , la forma general de la ecuación de Burgers, también conocida como «ecuación de Burgers viscosa», en una dimensión espacial en el sistema disipativo es:
Cuando el término de difusión está ausente es decir, cuando , la «ecuación de Burgers» se convierte en la «ecuación de Burgers inviscida»:
que es un prototipo para la ecuaciones de conservación que puede desarrollar discontinuidades, como la onda de choque. La ecuación anterior es la forma advectiva de la ecuación de Burgers. La "forma conservativa" es más útil en la integración numérica
Ecuación de Burgers no viscosa
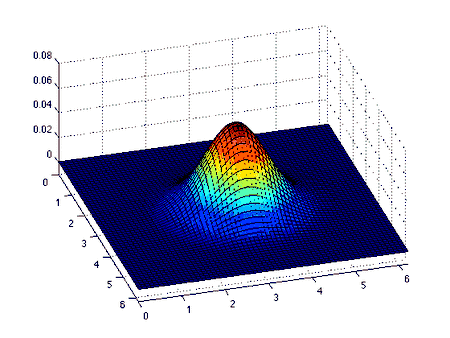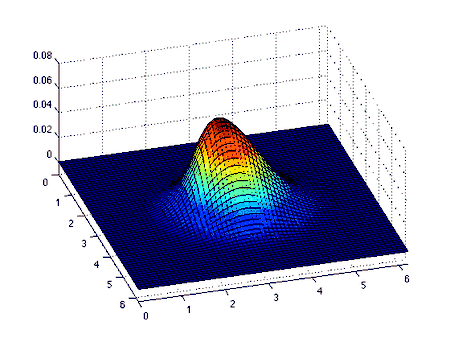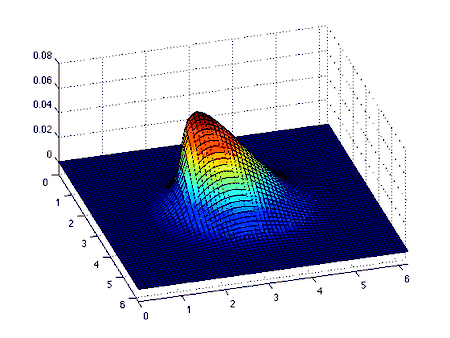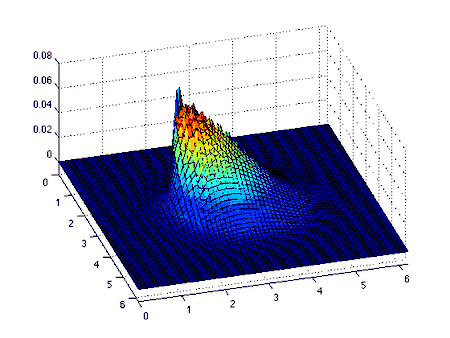
La ecuación de Burgers es una ecuaciones de conservación, más generalmente una ecuación hiperbólica «cuasi-lineal» de primer orden. La solución a la ecuación y junto con la siguiente condición inicial
puede construirse mediante el método de características. Las ecuaciones características son
La integración de la segunda ecuación nos dice que es constante a lo largo de la característica y la integración de la primera ecuación muestra que las características son rectas, es decir, integrando las ecuaciuón diferenciales anteriores, se obtienen respectivamente:
dónde es el punto (o parámetro) en el eje x-axis (t = 0) del plano x-t desde el que se dibuja la curva característica. Como en un punto la velocidad se conoce desde la condición inicial, y el hecho de que este valor no cambia a medida que avanzamos a lo largo de la característica que parte de ese punto, podemos escribir en esa característica. Por lo tanto, la trayectoria de esa característica es
Por lo tanto, la solución está dada por
Esta es una relación implícita que determina la solución de la ecuación inviscible de Burgers, siempre que las características no se crucen. Si las características se cruzan, entonces no existe una solución clásica para la ecuación en derivadas parciales y conduce a la formación de una onda de choque. De hecho, el tiempo de ruptura antes de que se pueda formar una onda de choque está dado por
Integral completa
Subrahmanyan Chandrasekhar proporcionó la solución explícita en 1943(En la decadencia de las ondas de choque del avión), cuando la condición inicial es lineal, es decir, donde a y b[6] la solución explícita es:
Esta solución también es la «integral completa» de la ecuación de Burgers inviscible porque contiene tantas constantes arbitrarias como el número de variables independientes que aparecen en la ecuación. [7] Las soluciones explícitas para otras condiciones iniciales relevantes son, en general, desconocidas.
Ecuación de Burgers viscosa
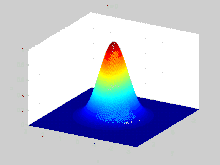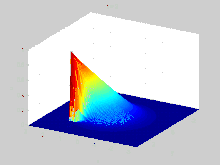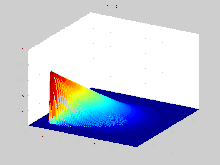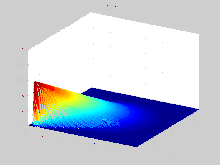
La ecuación viscosa de Burgers puede ser convertida en una ecuación lineal por la transformación Cole-Hopf.[7][8]
lo que la convierte en la ecuación:
que puede ser integrada con respecto a y se obtiene:
donde es una función que depende de las condiciones límites. Si de forma idéntica (por ejemplo, si el problema se va a resolver en un dominio periódico), entonces se obtiene la ecuación de difusión
La ecuación de difusión puede ser resuelta, y la transformación de Cole-Hopf invertida, para obtener la solución de la ecuación de Burgers:
Otras formas
Ecuación de Burgers generalizada
La ecuación de Burgers generalizada extiende la convectiva cuasilineal a una forma más generalizada, es decir,
donde es una función arbitraria de u. La ecuación inviscible sigue siendo una ecuación hiperbólica cuasilineal para y su solución puede hallarse usando método de características como antes.[9]
Ecuación de Burgers estocástica
Añadido el factor de ruido del espacio-tiempo la forma de la ecuación estocástica de Burgers[10]
Este PDE estocástico es la versión unidimensional de la ecuación de Kardar-Parisi-Zhang en un campo al sustituir .
Referencias
- Se relaciona con la ecuación de momento de Navier-Stokes con el término de presión eliminada Ecuación de Burgers (PDF): aquí la variable es la velocidad de flujo y = u Burgers Equation.: here the variable is the flow speed y=u
- Surge de la ecuación de Westervelt con una suposición de ondas de propagación estrictamente hacia adelante y el uso de una transformación de coordenadas a un marco de tiempo retardado: aquí la variable es la presión
- Bateman, H. (1915). Some recent researches on the motion of fluids. Monthly Weather Review, 43(4), 163-170.
- Whitham, G. B. (2011). Linear and nonlinear waves (Vol. 42). John Wiley & Sons.
- Burgers, J. M. (1948). A mathematical model illustrating the theory of turbulence. In Advances in applied mechanics (Vol. 1, pp. 171-199 ). Elsevier.
- Chandrasekhar, S. (1943). On the decay of plane shock waves (No. 423). Ballistic Research Laboratories.
- Julian Cole (1951). En una ecuación parabólica cuasi lineal que se produce en la aerodinámica. Trimestral de matemáticas aplicadas, 9(3), 225-236
- Eberhard Hopf (September 1950). «The partial differential equationy ut + uux = μuxx». Communications on Pure and Applied Mathematics 3 (3): 201-230. doi:10.1002/cpa.3160030302.
- Courant, R., & Hilbert, D. Methods of Mathematical Physics. Vol. II.
- W. Wang and A. J. Roberts. Diffusion approximation for self-similarity of stochastic advection in Burgers’ equation. Communications in Mathematical Physics, July 2014.
Enlaces externos
- Burgers' Equation at EqWorld: The World of Mathematical Equations.
- Burgers' Equation Archivado el 26 de junio de 2010 en Wayback Machine. at NEQwiki, the nonlinear equations encyclopedia.
- Burgers' Equation Wolfram|Alpha search results.