Ecuación de Mason-Weaver
La ecuación de Mason-Weaver describe la sedimentación y difusión de solutos bajo la acción de una fuerza uniforme, usualmente el campo gravitatorio.[1]
Ecuación
Suponiendo que el campo gravitatorio este alineado en la dirección z (Fig. 1), la ecuación de Mason-Weaver se escribe:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Tiempo | s | |
| Concentración de soluto (moles por unidad de longitud en la dirección z) | mol / m | |
| Constante de difusión del soluto | m2 / s | |
| Coeficiente de sedimentación | s | |
| Aceleración de la gravedad | m / s2 |
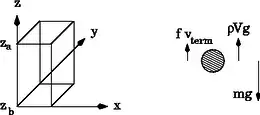
La ecuación de Mason-Weaver es complementada por las condiciones de contorno:
en la parte superior e inferior de la celda, indicadas como y , respectivamente (Fig. 1). Estas condiciones de contorno corresponden a los requerimientos físicos de que ningún soluto atraviesa la parte superior o inferior de la celda, o sea el flujo allí es cero. La celda se supone rectangular y alineada con los ejes cartesianos (Fig. 1), de forma que el flujo neto a través de las paredes lateral es también cero. Por lo tanto, la cantidad total de solución en la celda es:
y se conserva o sea .
Véase también
- Sedimentación
- Ecuación de Lamm
Referencias
- Mason, M; Weaver W (1924). «The Settling of Small Particles in a Fluid». Physical Review 23: 412-426.