Ecuación de primer grado

Este tipo de ecuaciones están incorporados en los Núcleos de Aprendizajes Prioritarios (NAP) para abordar en los primeros años de la Educación Secundaria para saber usar estrategias algebraicas para encontrar soluciones.[1]

Una ecuación de una variable ${\displaystyle mx+n=0}$ definida sobre un cuerpo ${\displaystyle \mathbb {K} }$, es decir, con ${\displaystyle \{m,n,x\}\subset \mathbb {K} ,m\neq 0}$ donde x es la variable, admite la siguiente solución:

Ejemplo: ecuación de una variable

${\displaystyle x=-{\frac {n}{m}}}$

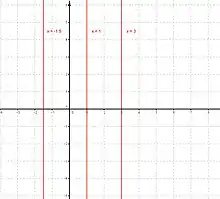
La solución de una ecuación lineal de una variable, se puede representar en una gráfica con una recta paralela al eje vertical

Cuando tanto la incógnita como los coeficientes son elementos de un anillo que no es un cuerpo, el asunto es más complicado ya que sólo existirán soluciones cuando m divide a n, si el anillo es un dominio de integridad:

${\displaystyle \exists k:n=m\cdot k\Rightarrow x=-k}$

Ejemplo gráfico de ecuaciones lineales.

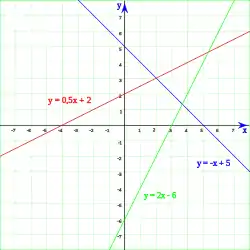
La incorporación de dos variables a las ecuaciones lineales produce que se puedan interpretar relaciones matemáticas entre ellas. La educación secundaria aborda este concepto a través de la modelización matemática de situaciones problemáticas.[2]

Una de las formas algebraicas más utilizada en las ecuaciones lineales de dos variables es :

${\displaystyle y=mx+n}$;

También se conoce como forma explícita.

Donde ${\displaystyle m}$ representa la pendiente y el valor de ${\displaystyle n}$ determina el punto donde la recta corta al eje Y (la ordenada al origen).

En el sistema cartesiano las ecuaciones lineales con dos incógnitas representan rectas.

Algunos ejemplos de ecuaciones lineales con dos incógnitas pueden ser los siguientes:

${\displaystyle 3x+2y=5}$

${\displaystyle 3x+y-5=-7x+4y+3}$

Algunos necesitan de la utilización de técnicas algebraicas para representarlas como la forma explícita de las rectas.[3]

Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.

• Ecuación general

${\displaystyle Ax+By+C=0}$

Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x y y se anulan.

• Ecuación segmentaria o simétrica
  

  Ejemplo de forma segmentaria:x/2 + y/3 = 1

${\displaystyle {\frac {x}{E}}+{\frac {y}{F}}=1}$

Aquí ni E ni F no pueden ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y F respectivamente.

• Forma paramétrica

1. ${\displaystyle x=Ut+x_{0}}$
2. ${\displaystyle y=Vt+y_{0}}$

Dos ecuaciones que deben cumplirse de manera simultánea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando. En esta representación puede afirmarse que la recta pasa por el punto ${\displaystyle (x_{0},y_{0})}$ y forma con el eje de abcisas un ángulo cuya tangente satisface: ${\displaystyle \tan \alpha =V/U}$

• Casos especiales:

${\displaystyle y=F}$ Un caso especial es la forma estándar donde ${\displaystyle A=0}$ y ${\displaystyle B=1}$ . El gráfico es una línea horizontal sin intersección con el eje X o (si F = 0) coincidente con ese eje

${\displaystyle x=E}$

Otro caso especial de la forma general donde ${\displaystyle A=1}$ y ${\displaystyle B=0}$. El gráfico es una línea vertical, interceptando el eje X en E.

${\displaystyle 0=0}$

En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.

Nótese que si la manipulación algebraica lleva a una ecuación como 1 = 0 entonces la original es llamada inconsistente, o sea que no se cumple para ningún par de números x e y. Un ejemplo podría ser: ${\displaystyle 3x+2=3x}$.

Adicionalmente podría haber más de dos variables, en ecuaciones simultáneas. Para más información véa: Sistema lineal de ecuaciones.

Las ecuaciones lineales de varias variables admiten también interpretaciones geométricas, cuando los coeficientes de la ecuación pertenecen a un cuerpo. Así una función lineal de dos variables de la forma siguiente

${\displaystyle f(x,y)=a_{1}x+a_{2}y}$

representa una recta en un plano. En varias variables asumiendo que tanto las variables ${\displaystyle x_{i}\in \mathbb {K} }$ y los coeficientes ${\displaystyle a_{i}\in \mathbb {K} }$, donde ${\displaystyle \mathbb {K} }$ es un cuerpo entonces una ecuación lineal como la siguiente:

${\displaystyle f(x_{1},x_{2},...,x_{n})=a_{1}x_{1}+a_{2}x_{2}+...+a_{n}x_{n}}$

representa un hiperplano de n-1 dimensiones en el espacio vectorial n-dimensional ${\displaystyle \mathbb {K} ^{n}}$.

Una función definida sobre un espacio vectorial es lineal si y solo si se cumple con la siguiente proposición:

${\displaystyle f(x+y)=f(x)+f(y)}$

${\displaystyle f(\alpha x)=\alpha f(x)}$

Donde α es cualquier escalar. También se llama a f operador lineal.

• Función lineal
• Ecuación de segundo grado
• Ecuación de tercer grado
• Ecuación de cuarto grado
• Ecuación de quinto grado
• Ecuación de sexto grado
• Ecuación de séptimo grado
• Ecuación de octavo grado