Ecuación de sexto grado

En matemáticas, una ecuación de sexto grado o ecuación séxtica es una ecuación polinómica de grado seis. Tiene la forma:

Ecuación de sexto grado

Gráfico de un polinomio de grado 6, con 5 puntos críticos.

Los coeficientes a, b, c, d, e, f, g son miembros de un cuerpo, (típicamente los números racionales, los números reales o los números complejos), y

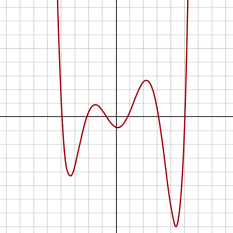
Debido a que tienen un grado par, las funciones normales de sexto grado parecen similares a las gráficas de las ecuaciones de cuarto grado normales, excepto en que pueden poseer máximos y mínimos locales adicionales. La derivada de una función de sexto orden es una función quíntica, mientras que su integral una función séptica.

Debido a que una función séxtica es un polinomio con grado par, tiene el mismo límite cuando su argumento tiende al infinito positivo o negativo. Si a es positivo, entonces la función se incrementa al infinito positivo en ambos lados; y así la función tiene un mínimo global. Así mismo, si a es negativo, la función disminuye al infinito negativo y tiene un máximo global.

Séxticos resolubles

Algunas ecuaciones de sexto grado pueden ser resueltas factorizándolas en radicales, pero en otras no es posible. Évariste Galois desarrolló técnicas para determinar si una ecuación dada podría ser resuelta por radicales que dieran lugar al campo de la teoría de Galois.[1]

Se desprende de la teoría de Galois que una ecuación de sexto grado es resoluble en términos de radicales si y solo si su [[grupo de ses importante las ecuaciones

para saber bien multiplicar permuta las raíces como las isometrías de un octaedro regular permutan sus vértices o en el grupo de orden 72 que estabiliza una partición del conjunto de las raíces en dos subconjuntos de tres raíces.

Hay fórmulas para probar cada caso y, si la ecuación es resoluble, computar las raíces en términos de radicales.[2]

La ecuación general de sexto grado puede ser resuelta en términos de funciones de Kampé de Fériet.[1] Una clase más restringida de ecuaciones de sexto grado puede ser resueltas en términos de funciones hipergeométricas generalizadas en una variable usando la aproximación de Felix Klein para resolver la ecuación de quinto grado.[1]


Véase también

Referencias
  1. Mathworld - Sextic Equation
  2. T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.