Efecto Eötvös
El efecto Eötvös es el cambio en la fuerza de la gravedad medida causado por el cambio en la aceleración centrífuga resultante del movimiento en dirección este u oeste del punto desde el que se efectúa la medida. Cuando el punto de observación se mueve hacia el este, la velocidad angular del objeto se incrementa (sumándose a la de rotación de la Tierra), y por lo tanto la fuerza centrífuga también aumenta, causando una reducción en la medición de la fuerza de gravedad.
Descubrimiento del efecto Eötvös
A principios de la década de 1900, un equipo alemán del Instituto de Geodesia de Potsdam realizó mediciones de la gravedad en buques en movimiento en los océanos Atlántico, Índico y Pacífico. Estudiando los resultados obtenidos, el físico húngaro Loránd Eötvös (1848-1919) se dio cuenta de que las lecturas fueron menores cuando el barco se movía hacia el este, y más altas cuando se movía hacia el oeste. Este hecho se identificó como una consecuencia de la rotación de la Tierra. En 1908, se realizaron nuevas mediciones en el Mar Negro con dos barcos: uno se movía hacia el este y el otro hacia el oeste. Los resultados obtenidos coincidían con las deducciones de Eötvös.[1]
Explicación física
El diseño más común de un gravímetro concebido para el trabajo de campo está basado en un muelle: algo tan simple como un resorte del que se suspende un peso interno. La fuerza de suspensión proporcionada por el muelle contrarresta la fuerza de la gravedad. Un resorte así fabricado tiene la propiedad de que la cantidad de fuerza que ejerce el resorte es proporcional a la extensión del muelle respecto a su longitud inicial (es decir, cuando no está cargado). Cuanto más fuerte es la gravedad efectiva en una ubicación particular, más se extiende el resorte: el muelle se extiende en la longitud necesaria para contrarrestar el efecto de la gravedad sobre el peso interno. Las partes móviles del gravímetro se montan en cápsulas rellenas de líquido para que el dispositivo sea menos susceptible a las influencias externas, tales como las vibraciones y los cambios de temperatura.
Formulación
Fórmula general
Desde entonces, en geodesia se utiliza la fórmula siguiente para corregir el efecto de la velocidad respecto a la Tierra durante una serie de mediciones:[2]
| Símbolo | Nombre |
|---|---|
| Velocidad angular de rotación de la Tierra | |
| Velocidad en la dirección latitudinal (este-oeste) | |
| Velocidad en la dirección longitudinal (norte-sur) | |
| Latitud en la que se toman las mediciones | |
| Radio de la Tierra |
El primer término de la fórmula, , corresponde al efecto Eötvös. El segundo término es un refinamiento que en circunstancias normales es mucho menor que el efecto Eötvös.
Primer término
El primer término de la fórmula del efecto Eötvös es proporcional a la componente de la fuerza centrípeta perpendicular a la superficie local de la Tierra (ligada a la latitud), y por lo tanto es descrita por una ley coseno: cuanto más cerca de la línea ecuatorial, mayor es la distancia al eje de la tierra (radio de giro) y más fuerte será el efecto.
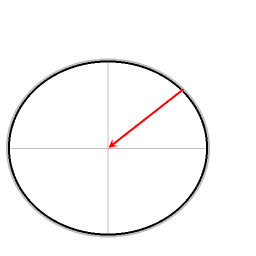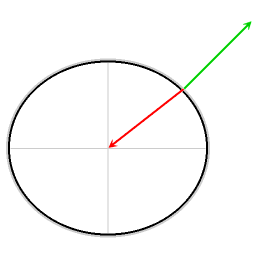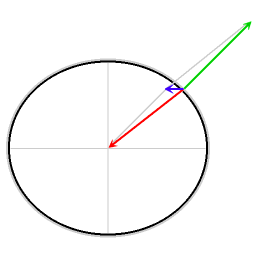
La deducción matemática del efecto Eötvös para el movimiento a lo largo de la línea del Ecuador, explica el factor 2 en el primer término de la fórmula (ver en el punto siguiente el desarrollo de la fórmula simplificada).
Debido a su rotación, la Tierra es de forma casi esférica (presentando un ligero abombamiento ecuatorial, que en este caso no se considera). La fuerza de gravedad se dirige hacia el centro de masas de la Tierra, y la fuerza normal es perpendicular a la superficie local.
En los polos y en el ecuador, la fuerza de la gravedad y la fuerza normal tienen exactamente la dirección opuesta. En todas las demás latitudes, las dos fuerzas no son exactamente opuestas, por lo que queda una fuerza resultante, que actúa hacia el eje de la Tierra. En cada latitud es precisamente la cantidad de fuerza centrípeta necesaria para mantener un espesor uniforme de la capa atmosférica. Por otro lado, la Tierra sólida es dúctil. Siempre que la forma de la Tierra sólida no está del todo en equilibrio con su velocidad de rotación, entonces un esfuerzo cortante la deforma en un período de millones de años hasta que se recupera el equilibrio.
Cuando una aeronave tiene una velocidad hacia el este (a favor del giro de la Tierra), adquiere un "exceso de velocidad". La situación es comparable a la de un coche de carreras en un velódromo con una superficie muy resbaladiza. Si el coche de carreras va demasiado rápido, entonces el coche tiende a salirse de la pista hacia arriba. Para una aeronave en vuelo, esto equivale a una reducción del peso, en comparación con el peso cuando la aeronave está en reposo con respecto a la Tierra.
Si a continuación la aeronave tiene una velocidad hacia el oeste, la situación es como la de un coche de carreras en un velódromo cuando va demasiado lento: en una superficie resbaladiza el coche va a desplomarse hacia abajo. Para una aeronave en vuelo esto significa un aumento del peso.
Segundo término
El segundo término representa la aceleración centrípeta requerida para que la aeronave siga la curvatura de la tierra. Es independiente tanto de la rotación de la Tierra como de la dirección del movimiento. Por ejemplo, cuando un avión que lleva instrumentos de lectura gravimétricos sobrevuela uno de los polos con altitud constante, la trayectoria del avión sigue la curvatura de la tierra. El primer término de la fórmula es cero, debido a que el coseno del ángulo es cero (en los polos ); entonces el segundo término representa la aceleración centrípeta necesaria para seguir la curvatura de la superficie de la Tierra a una velocidad dada.
Fórmula simplificada
Para un objeto en movimiento sobre el ecuador: Un sistema de referencia conveniente en esta situación es un sistema de coordenadas inercial que se desplace con el centro de masas de la Tierra. En esta situación, se puede afirmar que los objetos que están en reposo sobre la superficie de la Tierra (es decir, que giran conjuntamente con la Tierra), están dando vueltas eje de la Tierra, por lo que experimentan la correspondiente aceleración centrípeta con respecto a este sistema inercial de coordenadas.
Lo que se pretende determinar es la diferencia de la aceleración centrípeta de la aeronave cuando no se desplaza respecto a la Tierra, y cuando tiene una velocidad con respecto a la misma. La siguiente deducción es válida exclusivamente para el movimiento en dirección este-oeste (o también en dirección oeste-este, de signo contrario).
| Símbolo | Nombre | Fórmula |
|---|---|---|
| Aceleración centrípeta total cuando la aeronave se mueve a lo largo de la superficie de la Tierra | ||
| Aceleración centrípeta cuando la aeronave permanece estacionaria con respecto a la Tierra | ||
| Velocidad angular de la Tierra: una revolución por día sideral | ||
| Velocidad angular de la aeronave relativa a la velocidad angular de la Tierra | ||
| Velocidad angular total de la aeronave | ||
| Velocidad de la aeronave (velocidad relativa a la Tierra) | ||
| Radio de la Tierra |
Igualando fuerzas y operando, se tiene que:
Se puede ver fácilmente que en el caso de movimiento a lo largo del ecuador, la fórmula general se simplifica en la fórmula anterior:
- (para y )
Ejemplo práctico
Se va a calcular la magnitud del efecto Eötvös sobre unas mediciones de gravedad, suponiendo que:
Caso simplificado
Movimiento sobre el ecuador:
- -La masa interna del gravímetro es de 10 kilogramos
- -El gravímetro se desplaza en un dirigible sobrevolando el [Ecuador terrestre], con una velocidad de crucero uniforme de 25 metros por segundo (se desprecia la altura del dirigible)
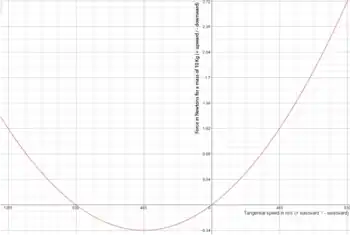
Cálculo: En el ecuador, la velocidad de la superficie de la Tierra es de unos 465 metros por segundo (una vuelta completa por el ecuador cada 24 horas: aproximadamente 40000000m/24h/60m/60s). La aceleración centrípeta resultante del giro de la Tierra, con un radio de 6378 kilómetros (radio ecuatorial de la Tierra) de la trayectoria circular del dirigible, es de:
o lo que es equivalente, es de aproximadamente 0.034 newton por kilogramo de masa. Para la masa de 10 kg, el efecto de la fuerza centrípeta asciende a aproximadamente 0.34 newton. La fuerza necesaria para mantener en suspensión la masa de la pesa interna de 10 kg (es decir, la lectura del gravímetro), se determina tomando la atracción gravitatoria (multiplicado la masa por la aceleración de la gravedad, que en este ejemplo se considera ) de 100 newtons, y restándole esos 0.34 newtons. En otras palabras: cualquier objeto que gira conjuntamente con la Tierra en el ecuador, tiene su peso medido reducido en un 0.34 por ciento, debido a la rotación de la Tierra.
Cuando se circula a 25m/s hacia el este, la velocidad total se convierte en 465+25=490m/s, lo que requiere una fuerza centrípeta de cerca de 0.375 newton (repitiendo el cálculo anterior, pero con v=490m/s). Cuando se circula a 25m/s hacia el oeste, la velocidad total se convierte en 465-25=440m/s, lo que requiere unos 0,305 newtons. En consecuencia, después de girar 180°, la lectura del gravímetro variará en un 0,7% (unos 7 gramos para la masa de 10 kg). En consecuencia, el muelle del gravímetro deberá extenderse un poco para acomodar un "peso" ligeramente mayor.
Caso general
Movimiento a lo largo del paralelo a 60 grados de latitud:
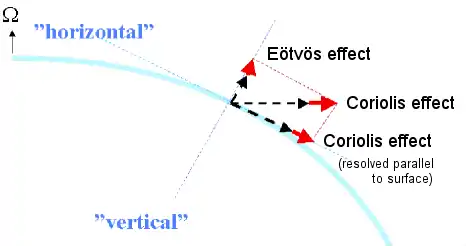
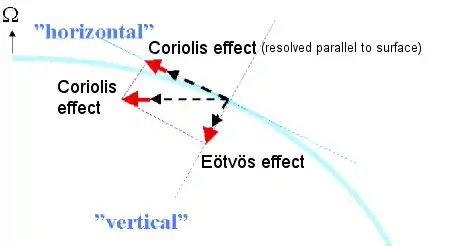
Se utiliza de nuevo el mismo gravímetro, con una masa interna de 10 kilogramos.
Cálculo de la reducción de peso en situación estacionaria respecto a la Tierra:
Un objeto situado a 60 grados de latitud, con el mismo movimiento que la Tierra, está siguiendo una trayectoria circular, con un radio de unos 3.190 kilómetros, y una velocidad de aproximadamente 233m/s (dado que , el radio es la mitad que el ecuatorial, y la velocidad también se reduce a la mitad que en el caso anterior, cuando el objeto estaba en el ecuador). Esa trayectoria circular requiere una fuerza centrípeta de alrededor de 0.017 newton por cada kilogramo de masa (=2332//3190000 = 0.17 m/s2) ; o lo que es lo mismo, 0.17 newton para el peso interno de 10 kilogramos. A los 60 grados de latitud, la componente de la aceleración centrípeta perpendicular a la superficie local (la vertical local) es la mitad de la fuerza total (otra vez interviene el coseno de 60°). Por lo tanto, a 60 grados de latitud, cualquier objeto en movimiento con la Tierra tiene su peso (inicialmente 100 newtons) reducido en aproximadamente un 0,08 por ciento (= 0.17 · cos 60), debido a la rotación de la Tierra.
Cálculo del efecto de Eötvös:
Cuando la aeronave se desplazaba a 25m/s hacia el este, la velocidad total se convierte en 233+25=258m/s, lo que requiere una fuerza centrípeta de cerca de 0.208 newton. Debido al coseno de 60°, la componente vertical local resultante es la mitad: 0.104 newton. Cuando la aeronave se desplazaba a 25m/s hacia el oeste, la velocidad total se convierte en 233-25=208m/s, lo que se traduce en una fuerza centrípeta de cerca de 0.135 newton. La componente vertical local resultante también es la mitad: 0.068 newton. De aquí se deduce que a 60 grados de latitud, la diferencia de peso de la masa de 10 kilogramos antes y después del cambio de sentido de la aeronave es de 1.7 gramos en el peso medido (de forma aproximada, la fuerza gravitatoria con la que la Tierra atrae una masa de un gramo -peso- equivale a un newton).
Los diagramas muestran también la componente tangente a la superficie local. En meteorología y en oceanografía, es habitual referirse a los efectos de la componente paralela a la superficie local como efecto Coriolis.
Otras aplicaciones
En meteorología, en modelos de alto rendimiento, se debe tener en cuenta el efecto Eötvos a escala terrestre. Las masas de aire pueden tener velocidades considerables con respecto a la superficie terrestre, lo que puede traducirse en una tendencia del aire a migrar a mayor altitud, lo que debe tenerse en cuenta cuando las exigencias de precisión son máximas.
Referencias
- An Intuitive Approach to the Coriolis Effect Kristian Silver. Bachelor Thesis in Meteorology. Department of Earth Sciences, Uppsala University. Texto completo en PDF
- The Coriolis Effect – a conflict between common sense and mathematics Anders Persson, The Swedish Meteorological and Hydrological Institute, Norrköping, Sweden
- El efecto Coriolis PDF-archivo. 870 KB 17 páginas. Una discusión general por el meteorólogo Anders Persson de diversos aspectos de la geofísica, cubriendo el efecto Coriolis, ya que se toma en cuenta en Meteorología y Oceanografía, el efecto de Eötvös, el péndulo de Foucault, y columnas de Taylor.
Enlaces externos
- En 1915 Eötvös construyó un dispositivo de sobremesa que demuestra el efecto de Eötvös. El dispositivo se encuentra entre otros instrumentos en la exhibición en un pequeño museo que se dedica a la obra y la vida de Eötvös.
- Foto ampliada del dispositivo de sobremesa de la página web del museo.