Eje óptico
Un eje óptico es una línea a lo largo de la cual existe cierto grado de simetría rotacional en un sistema óptico, como una lente de cámara, un microscopio o una mira telescópica.[1]
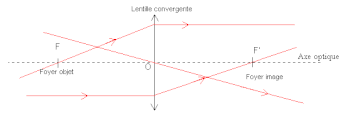
El eje óptico es una línea imaginaria que define el camino a lo largo del cual la luz se propaga a través del sistema, hasta una primera aproximación. Para un sistema compuesto por lentes y espejos simples, el eje pasa por el centro de curvatura de cada superficie y coincide con el eje de simetría rotacional. El eje óptico suele coincidir con el eje mecánico del sistema, pero no siempre, como en el caso de los sistemas ópticos fuera del eje. Para una fibra óptica, el eje óptico está a lo largo del centro del núcleo de la fibra y también se conoce como el eje de la fibra.[2]
Definición
El concepto de eje óptico no tiene razón de existir excepto en un sistema llamado "centrado", es decir, en que los diferentes elementos son rotacionalmente simétricos,[3][4] aunque no sean esféricos. Así, mientras una lente asférica con simetría de revolución no esté fuera de eje, el sistema puede considerarse de revolución y el eje óptico existe.[3][5]
Para los espejos, el eje óptico generalmente se define como la línea recta que conecta la parte superior del espejo y su centro de curvatura. Un rayo que pasa por el centro y el vértice se reflejará hacia el centro.[3] Tan pronto como se conserva la simetría de revolución, es posible hablar del eje óptico de un sistema, catóptrico, dióptrico o catadióptrico, también es posible analizar un sistema fuera del eje que contiene reflexiones considerando el sistema desplegado equivalente, devolviendo la combinación a un sistema de revolución.[6]
Más simplemente, el eje óptico es el eje que contiene todos los centros de curvatura de las superficies del sistema.[5]
Trazado de rayos
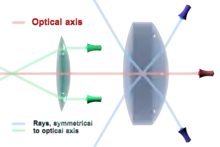
El eje óptico suele estar orientado de izquierda a derecha, y en un marco ortonormal es el eje (Oz),[6] su significado indica la dirección de propagación de la luz,[3] en realidad representa la trama de un rayo de luz que pasa por el centro del sistema y no desviarse durante el cruce en el caso de un sistema centrado.[4] Además, cualquier punto de objeto ubicado en el eje se refleja en el eje y los puntos focales del sistema se colocan en el eje óptico.
En el marco de la aproximación gaussiana, los rayos se consideran cercanos y ligeramente inclinados con respecto al eje óptico[4] y se denominan "rayos paraxiales"[5] ahí el nombre "óptica paraxial" designando el campo de la óptica geométrica cubierto por la aproximación gaussiana.
El eje óptico también permite definir los planos meridianos, planos que contienen este eje y el "rayos meridianos" contenidos en estos planos, a diferencia de los "rayos oblicuos"; los rayos de luz que pasan a través de un punto del objeto que pertenece al eje óptico son "rayos axiales".[6][5]
Además de los tipos de rayos de un sistema, el eje óptico define otros elementos, en particular la pupila de entrada y la pupila de salida de la combinación, situadas respectivamente en la intersección de la línea que lleva el rayo principal en el espacio objeto con el eje óptico, y en la intersección de la línea que lleva el rayo principal en el espacio de la imagen con el eje óptico siendo el rayo principal el rayo que pasa por el centro del diafragma de la combinación óptica.[5]
Aberraciones
Es posible clasificar las aberraciones ópticas de muchas maneras, incluso separándolas en aberraciones fuera del eje y aberraciones en el eje.[7] Algunas aberraciones existen exclusivamente en todos los puntos del espacio de la imagen, excepto el eje óptico: están fuera del eje. Las demás son aberraciones existentes en todo el espacio, incluido el eje óptico. En el eje, encontraremos así la aberración esférica y el cromatismo axial.[5][7] Las demás aberraciones tienen un comportamiento en el que cuanto más se aleja un punto del eje, mayores se presentan.[5]
Otros sistemas
Para una fibra óptica, el eje óptico o eje de la fibra sigue el centro del núcleo de la fibra y, por lo tanto, no es necesariamente una línea recta. Esta definición se aplica generalmente a todas las guías de ondas ópticas.[8] Siendo el eje óptico una invariante práctica en un sistema, también permite definir los gradientes de índice: a lo largo del eje óptico el gradiente se llama gradiente axial, y si es perpendicular al eje, gradiente radial.[5]
Referencias
- «Dictionary of Military Terms».
- «Optical axis definition». Archivado desde el original el 1 de marzo de 2011. Consultado el 18 de septiembre de 2022.
- Balland, Bernard (2007). Optique géométrique : imagerie et instruments. Presses polytechniques et universitaires romandes. ISBN 978-2-88074-689-6. OCLC 228785208.
- H Prépa, première année, p.50,
- Malacara, Zacarias (2013). Handbook of optical design (3rd ed edición). CRC Press. ISBN 1-4398-6799-2. OCLC 862237908.
- Bass, Michael; Optical Society of America (©1995-©2001). Handbook of optics (2nd ed. edición). McGraw-Hill. ISBN 0-07-047740-X. OCLC 30593527.
- Society of Photo-optical Instrumentation Engineers, Max J. (2001). Optical design fundamentals for infrared systems (2nd ed edición). SPIE. ISBN 978-0-8194-8069-9. OCLC 606666338.
- Hanson, A. G. (1982). Optical Waveguide Communications Glossary (en inglés). Information Gatekeepers Inc. p. 41.