Elasticidad del caucho

Fig. 1 Tensión frente a deformación por tracción para una red de caucho natural. Datos experimentales de Treloar (azul sólido), simulación teórica (rojo discontinuo)

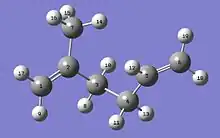
El Paradigma Molecular Kink procede de la noción intuitiva de que las cadenas moleculares que componen una red de caucho natural (poliisopreno) están restringidas por las cadenas circundantes para permanecer dentro de un "tubo". Las fuerzas elásticas producidas en una cadena, como resultado de alguna tensión aplicada, se propagan a lo largo del contorno de la cadena dentro de este tubo. La Fig. 2 muestra una representación de una unidad principal de isopreno de cuatro carbonos con un átomo de carbono extra en cada extremo para indicar sus conexiones con unidades adyacentes en una cadena. Tiene tres enlaces simples C-C y un enlace doble. Es principalmente al girar alrededor de los enlaces simples C-C que una cadena de poliisopreno explora aleatoriamente sus posibles conformaciones. Las secciones de la cadena que contienen entre dos y tres unidades de isopreno tienen suficiente flexibilidad para que puedan considerarse estadísticamente descorrelacionadas entre sí. Es decir, no hay correlación direccional a lo largo de la cadena para distancias mayores que esta distancia, denominada longitud de Kuhn. Estas regiones no rectas evocan el concepto de "torceduras" y, de hecho, son una manifestación de la naturaleza Caminata aleatoria de la cadena. Dado que una torcedura se compone de varias unidades de isopreno, cada una de las cuales tiene tres enlaces simples carbono-carbono, hay muchas conformaciones posibles disponibles para una torcedura, cada una con una energía distinta y una distancia de extremo a extremo. En escalas de tiempo de segundos a minutos, solo estas secciones relativamente cortas de la cadena, es decir, las torceduras, tienen suficiente volumen para moverse libremente entre sus posibles conformaciones rotacionales. Las interacciones térmicas tienden a mantener las torceduras en un estado de flujo constante, ya que realizan transiciones entre todas sus posibles conformaciones rotacionales. Debido a que las torceduras están en equilibrio térmico, la probabilidad de que una torcedura resida en cualquier conformación rotacional está dada por una distribución de Boltzmann y podemos asociar una entropía con su extremo a extremo distancia. La distribución de probabilidad para la distancia de extremo a extremo de una longitud de Kuhn es aproximadamente Gaussiana y está determinada por los factores de probabilidad de Boltzmann para cada estado (conformación rotacional). A medida que se estira una red de goma, algunas torceduras se fuerzan en un número restringido de conformaciones más extendidas que tienen una mayor distancia de extremo a extremo y es la disminución resultante de la entropía lo que produce una fuerza elástica a lo largo de la cadena.

Hay tres mecanismos moleculares distintos que producen estas fuerzas, dos de los cuales surgen de cambios en la entropía a los que nos referiremos como régimen de extensión de cadena baja, Ia[5] y régimen moderado de extensión de cadena, Ib.[6] El tercer mecanismo se produce en la extensión de cadena alta, ya que se extiende más allá de su longitud de contorno de equilibrio inicial por el distorsión de los enlaces químicos a lo largo de su columna vertebral. En este caso, la fuerza restauradora es de tipo resorte y nos referiremos a ella como régimen II.[7] Se encontró que los tres mecanismos de fuerza corresponden aproximadamente a las tres regiones observadas en los experimentos de tensión de tracción frente a deformación, se muestra en la figura 1.

La morfología inicial de la red, inmediatamente después del entrecruzamiento químico, se rige por dos procesos aleatorios:[8][9] (1) La probabilidad de que se produzca un entrecruzamiento en cualquier unidad de isopreno y (2) la naturaleza del recorrido aleatorio del conformación de la cadena. La distancia de extremo a extremo distribución de probabilidad para una longitud de cadena fija, es decir, un número fijo de unidades de isopreno, se describe mediante un recorrido aleatorio. Es la distribución de probabilidad conjunta de las longitudes de la cadena de la red y las distancias de extremo a extremo entre sus nodos de enlace cruzado lo que caracteriza la morfología de la red. Debido a que tanto los mecanismos de física molecular que producen las fuerzas elásticas como la morfología compleja de la red deben tratarse simultáneamente, los modelos de elasticidad analíticos simples no son posibles; un modelo numérico tridimensional explícito[10][11][12] para simular los efectos de la tensión en un elemento de volumen representativo de una red.

El Paradigma Molecular Kink visualiza una cadena de red representativa como una serie de vectores que siguen el contorno de la cadena dentro de su tubo. Cada vector representa la distancia de equilibrio de extremo a extremo de una torcedura. La trayectoria tridimensional real de la cadena no es pertinente, ya que se supone que todas las fuerzas elásticas operan a lo largo del contorno de la cadena. Además de la longitud del contorno de la cadena, el único otro parámetro importante es su tortuosidad, la relación entre la longitud de su contorno y su distancia de extremo a extremo. A medida que se extiende la cadena, en respuesta a una deformación aplicada, se supone que la fuerza elástica inducida se propaga uniformemente a lo largo de su contorno. Considere una cadena de red cuyos puntos finales (nodos de red) están más o menos alineados con el eje de deformación por tracción. A medida que se aplica la tensión inicial a la muestra de caucho, los nodos de la red en los extremos de la cadena comienzan a separarse y todos los vectores de torcedura a lo largo del contorno se estiran simultáneamente. Físicamente, la tensión aplicada obliga a las torceduras a estirarse más allá de su equilibrio térmico distancias de extremo a extremo, provocando una disminución en su entropía. El aumento de energía libre asociado con este cambio de entropía da lugar a una fuerza elástica (lineal) que se opone a la deformación. La constante de fuerza para el régimen de baja deformación se puede estimar mediante el muestreo de dinámica molecular (MD) trayectorias de una torcedura, es decir, cadenas cortas, compuestas de 2–3 unidades de isopreno, a temperaturas relevantes, p. 300K.[5] Al tomar muchas muestras de las coordenadas en el transcurso de las simulaciones, se pueden obtener las distribuciones de probabilidad de la distancia de extremo a extremo para una torcedura. Dado que estas distribuciones (que resultan ser aproximadamente Gaussiana) están directamente relacionadas con el número de estados, podemos asociarlas con la entropía de la torcedura en cualquier distancia de extremo a extremo. Al diferenciar numéricamente la distribución de probabilidad, se puede encontrar el cambio en la entropía y, por lo tanto, energía libre de Helmholtz, con respecto a la distancia de extremo a extremo de la torcedura. Se encuentra que el modelo de fuerza para este régimen es lineal y proporcional a la temperatura dividida por la tortuosidad de la cadena.

Fig. 2 Unidad principal de isopreno. compuesto por átomos de carbono (gris oscuro) y átomos de hidrógeno (blanco). Los átomos de carbono etiquetados como '1' y '6' están en unidades adyacentes en la cadena del polímero.

En algún punto del régimen de baja extensión, es decir, cuando todas las torceduras a lo largo de la cadena se extienden simultáneamente, se vuelve energéticamente más favorable tener una transición de torcedura a una conformación extendida para estirar más la cadena. La tensión aplicada puede obligar a una sola unidad de isopreno dentro de una torcedura a adoptar una conformación extendida, aumentando ligeramente la distancia de extremo a extremo de la cadena, y la energía requerida para hacer esto es menor que la necesaria para continuar extendiendo todas las torceduras simultáneamente. . Numerosos experimentos[13] sugieren fuertemente que el estiramiento de una red de caucho va acompañado de una disminución de la entropía. Como se muestra en la Fig. 2, una unidad de isopreno tiene tres enlaces C-C simples y hay dos o tres ángulos de rotación preferidos (orientaciones) sobre estos enlaces que tienen mínimos de energía. De las 18 conformaciones rotacionales permitidas, solo 6 tienen distancias de extremo a extremo extendidas y obligar a las unidades de isopreno en una cadena a residir en algún subconjunto de los estados extendidos debe reducir el número de conformaciones rotacionales disponibles para térmica. movimiento. Es esta reducción en el número de estados disponibles lo que hace que la entropía disminuya. A medida que la cadena continúa enderezándose, todas las unidades de isopreno en la cadena finalmente se fuerzan a adoptar conformaciones extendidas y se considera que la cadena está "tensa". Se puede estimar una constante de fuerza para la extensión de la cadena a partir del cambio resultante en energía libre asociado con este cambio de entropía.[6] Al igual que con el régimen Ia, el modelo de fuerza para este régimen es lineal y proporcional a la temperatura dividida por la tortuosidad de la cadena.

Cuando todas las unidades de isopreno en una cadena de red se han visto obligadas a residir en solo unas pocas conformaciones rotacionales extendidas, la cadena se vuelve tensa. Puede considerarse sensiblemente recto, excepto por el camino en zigzag que hacen los enlaces C-C a lo largo del contorno de la cadena. Sin embargo, aún es posible una mayor extensión mediante distorsiones de enlace, por ejemplo, aumentos del ángulo de enlace, estiramientos de enlace y rotaciones del ángulo diedro. Estas fuerzas son similares a resortes y no están asociadas con cambios de entropía. Una cadena tensa puede extenderse solo un 40%. En este punto, la fuerza a lo largo de la cadena es suficiente para romper mecánicamente el enlace covalente C-C. Este límite de fuerza de tracción se ha calculado[7] a través de simulaciones de química cuántica y es de aproximadamente 7 n N, aproximadamente un factor de mil mayor que las fuerzas de la cadena entrópica a baja tensión. Los ángulos entre los enlaces C-C de la columna vertebral adyacente en una unidad de isopreno varían entre aproximadamente 115 y 120 grados y las fuerzas asociadas con el mantenimiento de estos ángulos son bastante grandes, por lo que dentro de cada unidad, la columna vertebral de la cadena siempre sigue un camino en zigzag, incluso en la ruptura del enlace. Este mecanismo explica el fuerte aumento en la tensión elástica, observado en altas deformaciones (Fig. 1).

Aunque la red está completamente descrita por solo dos parámetros (el número de nodos de la red por unidad de volumen y la longitud de descorrelación estadística del polímero, la longitud de Kuhn), la forma en que se conectan las cadenas es en realidad bastante Complicado. Existe una amplia variación en las longitudes de las cadenas y la mayoría de ellas no están conectadas al nodo de red vecino más cercano. Tanto la longitud de la cadena como su distancia de extremo a extremo se describen mediante distribuciones de probabilidad. El término 'morfología' se refiere a esta complejidad. Si el agente de reticulación se mezcla completamente, existe la misma probabilidad de que cualquier unidad de isopreno se convierta en un nodo de red. Para el peróxido de dicumilo, la eficiencia de reticulación en el caucho natural es la unidad,[14] pero este no es el caso del azufre.[15] La morfología inicial de la red está dictada por dos procesos aleatorios: la probabilidad de que ocurra un entrecruzamiento en cualquier unidad de isopreno y la naturaleza de paseo aleatorio de Markov de una conformación de la cadena.[8][9] La función de distribución de probabilidad de hasta qué punto un extremo de una cadena puede 'desviarse' del otro se genera mediante una secuencia de Markov.[16] Esta función de densidad de probabilidad condicional relaciona la longitud de la cadena ${\displaystyle n}$ en unidades de la longitud de Kuhn ${\displaystyle b}$ a la distancia de extremo a extremo ${\displaystyle r}$:

$${\displaystyle P(r,N)\;=\;P(N)P(r|N)\;=\;p_{x}{\left(1-p_{x}\right)}^{N-1}\,4\pi r^{2}\left({\frac {2nb^{2}\pi }{3}}\right)^{-{3}/{2}}\exp \left(-{\frac {3r^{2}}{2nb^{2}}}\right)}$$

(4)

La probabilidad de que cualquier unidad de isopreno se convierta en parte de un nodo de enlace cruzado es proporcional a la proporción de las concentraciones de las moléculas de enlace cruzado (por ejemplo, peróxido de dicumilo) a las unidades de isopreno:

$${\displaystyle p_{x}=2{\frac {\text{[entrecruzamiento]}}{\text{[isopreno]}}}}$$

El factor de dos surge porque dos unidades de isopreno (una de cada cadena) participan en el entrecruzamiento. La probabilidad para encontrar una cadena que contenga ${\displaystyle N}$ unidades de isopreno está dada por:

$${\displaystyle P(N)=p_{x}{\left(1-p_{x}\right)}^{N-1}\,,}$$

(3)

where ${\displaystyle N\geq 1}$. La ecuación puede entenderse simplemente como la probabilidad de que una unidad de isopreno NO sea un enlace cruzado (1−p_x) en N−1 unidades sucesivas a lo largo de una cadena. Dado que P(N) disminuye con N, las cadenas más cortas son más probables que las más largas. Tenga en cuenta que el número de segmentos de la columna vertebral estadísticamente independientes no es el mismo que el número de unidades de isopreno. Para las redes de caucho natural, la longitud de Kuhn contiene alrededor de 2,2 unidades de isopreno, por lo que ${\displaystyle N\sim 2,2n}$. Es el producto de las ecuaciones (1) y (3) (la distribución de probabilidad conjunta) que relaciona la longitud de la cadena de la red (${\displaystyle N}$ ) y la distancia de extremo a extremo (${\displaystyle r}$) entre sus nodos de enlace cruzado de terminación:

$${\displaystyle P(r,N)\;=\;P(N)P(r|N)\;=\;p_{x}{\left(1-p_{x}\right)}^{N-1}\,4\pi r^{2}\left({\frac {2nb^{2}\pi }{3}}\right)^{-{3}/{2}}\exp \left(-{\frac {3r^{2}}{2nb^{2}}}\right)}$$

(4)

Fig. 3 Densidad de probabilidad para una cadena de red promedio frente a la distancia de extremo a extremo en unidades de espaciado medio de nodos de entrecruzamiento (2,9 nm); n= 52, b= 0,96 nm.

La morfología compleja de una red de caucho natural se puede ver en la Fig. 3, que muestra la densidad de probabilidad frente a la distancia de extremo a extremo (en unidades de espaciado medio de nodos) para una cadena "promedio". Para la densidad de entrecruzamiento experimental común de 4x10¹⁹ cm⁻³, una cadena promedio contiene aproximadamente 116 unidades de isopreno (52 longitudes de Kuhn) y tiene una longitud de contorno de aproximadamente 50nm. La Fig. 3 muestra que una fracción significativa de las cadenas abarca varios espaciamientos de nodos, es decir, los extremos de la cadena se superponen a otras cadenas de la red. El caucho natural, entrecruzado con peróxido de dicumilo, tiene entrecruzamientos tetrafuncionales, es decir, cada nodo entrecruzado tiene 4 cadenas de red que emanan de él. Dependiendo de su tortuosidad inicial y la orientación de sus puntos finales con respecto al eje de deformación, cada cadena asociada con un nodo de entrecruzamiento activo puede tener una constante de fuerza elástica diferente a medida que resiste la deformación aplicada. Para preservar el equilibrio de fuerzas (fuerza neta cero) en cada nodo de entrecruzamiento, se puede obligar a un nodo a moverse junto con la cadena que tiene la constante de fuerza más alta para la extensión de la cadena. Es este movimiento de nodo complejo, que surge de la naturaleza aleatoria de la morfología de la red, lo que hace que el estudio de las propiedades mecánicas de las redes de caucho sea tan difícil. A medida que se tensa la red, emergen caminos compuestos por estas cadenas más extendidas que abarcan toda la muestra, y son estos caminos los que llevan la mayor parte de la tensión a altas deformaciones.

Para calcular la respuesta elástica de una muestra de caucho, los tres modelos de fuerza de cadena (regímenes Ia, Ib y II) y la morfología de la red deben combinarse en un modelo de red micromecánica.[10][11][12] Usando la distribución de probabilidad conjunta en la ecuación (4) y los modelos de extensión de fuerza, es posible diseñar algoritmos numéricos para construir un elemento de volumen representativo fiel de una red y para simular la tensión mecánica resultante cuando se somete a tensión. Se utiliza un algoritmo de relajación iterativo para mantener el equilibrio de fuerza aproximado en cada nodo de la red a medida que se impone la tensión. Cuando la constante de fuerza obtenida para torceduras que tienen 2 o 3 unidades de isopreno (aproximadamente una longitud de Kuhn) se usa en simulaciones numéricas, se encuentra que la tensión predicha es consistente con los experimentos. Los resultados de dicho cálculo[15] se muestran en la Fig. 1 (línea roja discontinua) para el caucho natural reticulado con azufre y se comparan con los datos experimentales[17] (línea azul continua). Estas simulaciones también predicen un aumento pronunciado de la tensión a medida que las cadenas de la red se tensan y, en última instancia, la falla del material debido a la ruptura de la unión. En el caso del caucho natural entrecruzado con azufre, los enlaces S-S en el entrecruzamiento son mucho más débiles que los enlaces C-C en la columna vertebral de la cadena y son los puntos de falla de la red. La meseta en la tensión simulada, a partir de una tensión de alrededor de 7, es el valor límite de la red. No se pueden soportar tensiones superiores a unos 7 MPa y la red falla. Cerca de este límite de tensión, las simulaciones predicen[12] que menos del 10 % de las cadenas están tensas, es decir, en el régimen de extensión de cadena alta y menos del 0,1 % de las cadenas se han roto. Si bien la fracción de ruptura muy baja puede parecer sorprendente, no es inconsistente con nuestra experiencia de estirar una banda elástica hasta que se rompa. La respuesta elástica de la goma tras la rotura no difiere notablemente de la original.