Endurecimiento del borde de grano

El endurecimiento del borde de grano (o endurecimiento de Hall-Petch) es un método para mejorar la resistencia de un material mediante el cambio del tamaño de su cristalito (grano) promedio. Se basa en la observación de que los bordes de los granos son fronteras infranqueables para las dislocaciones y que la cantidad de dislocación dentro de un grano tiene un efecto sobre cómo se acumula la tensión en el grano adyacente, lo que finalmente activará las fuentes de dislocación y, por lo tanto, permitirá la deformación en el grano vecino también. Entonces, al cambiar el tamaño del grano, se puede influir en el número de dislocaciones acumuladas en el límite de cada grano y su fluencia. Por ejemplo, aplicar un tratamiento térmico después de la deformación plástica y cambiar la tasa de solidificación son formas de alterar el tamaño del grano.[1]

Figura 1: El endurecimiento de Hall-Petch está limitado por el tamaño de las luxaciones. Una vez que el tamaño de grano alcanza aproximadamente 10 nanómetros, los bordes del grano comienzan a deslizarse

Teoría

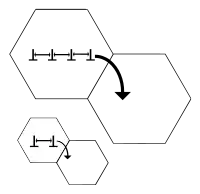
El endurecimiento de los bordes de los granos los transforma en puntos de fijación, impidiendo una mayor propagación de la dislocación. Dado que la estructura reticular de los granos adyacentes difiere en orientación, se requiere más energía para que una dislocación cambie de dirección y se mueva hacia el grano adyacente. El límite de grano también está mucho más desordenado que dentro del grano, lo que también evita que las dislocaciones se muevan en un plano de deslizamiento continuo. Impedir este movimiento de dislocación dificultará el inicio de la plastificación y, por lo tanto, aumentará el límite elástico del material.

Bajo una tensión aplicada, las dislocaciones existentes y las dislocaciones generadas por una fuente de Frank-Read se moverán a través de una red cristalina hasta encontrar un límite de grano, donde la gran falta de coincidencia atómica entre diferentes granos crea un campo de tensión repulsiva para oponerse al movimiento continuo de dislocación. A medida que se propagan más dislocaciones a este límite, se produce un "apilamiento" de dislocaciones, ya que un grupo de dislocaciones no puede moverse más allá del límite. Como las dislocaciones generan campos de tensión repulsivos, cada dislocación sucesiva aplicará una fuerza repulsiva a la dislocación incidente con el límite de grano. Estas fuerzas repulsivas actúan como una fuerza motriz para reducir la barrera energética para la difusión a través del límite, de modo que un apilamiento adicional provoca la difusión de dislocaciones a través del límite de grano, lo que permite una mayor deformación en el material. La disminución del tamaño de grano disminuye la cantidad de acumulación posible en el límite, lo que aumenta la cantidad de tensión aplicada necesaria para mover una dislocación a través de un límite de grano. Cuanto mayor sea la tensión aplicada necesaria para mover la dislocación, mayor será el límite elástico. Por lo tanto, existe una relación inversa entre el tamaño de grano y el límite elástico, como lo demuestra la ecuación de Hall-Petch. Sin embargo, cuando hay un gran cambio de dirección en la orientación de dos granos adyacentes, es posible que la dislocación no se mueva necesariamente de un grano al otro, sino que cree una nueva fuente de dislocación en el grano adyacente. La teoría sigue siendo la misma, de forma que más límites de grano crean más oposición al movimiento de dislocación y, a su vez, fortalecen el material.

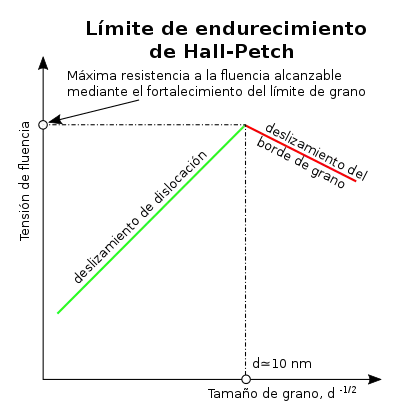
Obviamente, hay un límite para este modo de endurecimiento, ya que no existen materiales infinitamente resistentes. Los tamaños de grano pueden variar desde aproximadamente 100 micrómetros (granos grandes) hasta 1 micrómetro (granos pequeños). Por debajo de esto, el tamaño de las dislocaciones comienza a acercarse al tamaño de los granos. Con un tamaño de grano de aproximadamente 10 nanómetros,[2] solo una o dos dislocaciones pueden caber dentro de un grano (consúltese la Figura 1 anterior). Este esquema prohíbe la acumulación de dislocaciones y, en cambio, da como resultado la difusión del límite de grano. La red resuelve la tensión aplicada mediante el deslizamiento del límite de grano, lo que da como resultado una "disminución" del límite elástico del material.

Para comprender el mecanismo del endurecimiento del límite de grano, se debe comprender la naturaleza de las interacciones dislocación-dislocación. Las dislocaciones crean un campo de tensión a su alrededor dado por:

\sigma \propto {\frac {Gb}{r}},

donde G es el módulo de cizalladura del material, b es el vector de Burgers y r es la distancia desde la dislocación. Si las dislocaciones están correctamente alineadas entre sí, los campos de tensión locales que crean se repelerán entre sí. Esto ayuda al movimiento de dislocaciones en los granos y a través de los límites de los granos. Por lo tanto, cuantas más dislocaciones estén presentes en un grano, mayor será el campo de tensión recibido por una dislocación cerca de un límite de grano:

\tau _{\text{felt}}=\tau _{\text{applied}}+n_{\text{dislocation}}\tau _{\text{dislocation}}\,

Este es un esquema que ilustra aproximadamente el concepto de acumulación de dislocaciones y cómo afecta a la resistencia del material. Un material con un tamaño de grano más grande puede tener más dislocaciones acumuladas, lo que lleva a una mayor fuerza impulsora para que las dislocaciones se muevan de un grano a otro. Por lo tanto, se tendrá que aplicar menos fuerza para mover una dislocación de un grano más grande que de uno más pequeño, lo que lleva a los materiales con granos más pequeños a exhibir un límite elástico más alto

Endurecimiento de subgranos

Un subgrano es una parte del grano que está ligeramente desorientada con respecto a otras partes del grano.[3] Actualmente se están realizando investigaciones para ver el efecto del endurecimiento del subgrano en los materiales. Dependiendo del procesamiento del material, se pueden formar subgranos dentro de sus granos. Por ejemplo, cuando el material a base de hierro se muele con bolas durante largos períodos de tiempo (por ejemplo, más de 100 horas), se forman subgranos de 60 a 90 nm. Se ha demostrado que cuanto mayor es la densidad de los subgranos, mayor es el límite elástico del material debido al aumento del límite del subgrano. Se encontró que la resistencia del metal varía recíprocamente con el tamaño del subgrano, lo cual es análogo a la ecuación de Hall-Petch. El endurecimiento del límite del subgrano también tiene un punto de ruptura de alrededor de un tamaño de subgrano de 0.1 µm, que es el tamaño donde cualquier subgrano más pequeño que ese tamaño disminuye el límite elástico.[4]

Relación de Hall-Petch

Constantes de Hall–Petch[5]
Material	σ₀ [MPa]	k [MPa m^1/2]
Cobre	25	0.12
Titanio	80	0.40
Acero dulce	70	0.74
Ni₃Al	300	1.70

Existe una relación inversa entre el límite elástico delta y el tamaño de grano elevado a alguna potencia, x.

\Delta \tau \propto {k \over d^{x}}

donde k es el coeficiente de refuerzo y tanto k como x son específicos del material. Suponiendo una distribución de tamaño de grano monodispersa estrecha en un material policristalino, cuanto menor sea el tamaño de grano, menor será la tensión de repulsión que recibe una dislocación del límite de grano y mayor será la tensión aplicada necesaria para propagar las dislocaciones a través del material.

La relación entre el límite elástico y el tamaño de grano se describe matemáticamente mediante la ecuación de Hall-Petch:[6]

\sigma _{\text{y}}=\sigma _{0}+{k_{\text{y}} \over {\sqrt {d}}}

donde σ_y es el límite elástico, σ₀ es una constante de materiales para el esfuerzo inicial para el movimiento de dislocación (o la resistencia de la red al movimiento de dislocación), k_y es el coeficiente de refuerzo (a constante específica de cada material), y d es el diámetro medio del grano. Es importante tener en cuenta que la relación HP es un ajuste empírico a los datos experimentales, y que la noción de que una longitud de acumulación de la mitad del diámetro del grano causa una tensión crítica para la transmisión o generación en un grano adyacente de la microestructura no ha sido verificada por observación real.

Teóricamente, un material podría hacerse infinitamente resistente si los granos se hicieran infinitamente pequeños. Sin embargo, esto es imposible, porque el límite inferior del tamaño de grano es una sola celda unitaria del material. Incluso entonces, si los granos de un material tienen el tamaño de una sola celda unitaria, entonces el material es amorfo, no cristalino, ya que no hay un orden de largo alcance y las dislocaciones no se pueden definir en un material amorfo. Se ha observado experimentalmente que la microestructura con el límite elástico más alto es un tamaño de grano de aproximadamente 10 nm, porque los granos más pequeños que este experimentan otro mecanismo de fluencia, el deslizamiento de borde de grano.[2] Producir materiales de ingeniería con este tamaño de grano ideal es difícil porque solo se pueden producir películas delgadas de manera fiable con granos de este tamaño. En materiales que tienen una distribución de tamaño de grano bidispersa, por ejemplo, aquellos que exhiben crecimiento anormal del grano, los mecanismos de endurecimiento no siguen estrictamente la relación de Hall-Petch y se observa un comportamiento divergente.

Historia

A principios de la década de 1950, se escribieron de forma independiente dos series innovadoras de artículos sobre la relación entre los límites de grano y la resistencia.

En 1951, mientras estaba en la Universidad de Sheffield, E. O. Hall escribió tres artículos que aparecieron en el volumen 64 de los Proceedings of the Physical Society. En su tercer artículo, Hall[7] mostró que la longitud de las bandas de deslizamiento o la longitud de las grietas corresponden a los tamaños de grano y, por lo tanto, se puede establecer una relación entre los dos. Hall se concentró en las propiedades prácticas de los aceros al carbono.

Basado en su trabajo experimental realizado en 1946-1949, N. J. Petch de la Universidad de Leeds, Inglaterra, publicó un artículo en 1953 independiente del de Hall. El artículo de Petch[8] se concentró más en el fenómeno de la fractura. Al medir la variación en la resistencia a la escisión con respecto al tamaño de grano en los materíales ferríticos a temperaturas muy bajas, Petch encontró una relación exacta a la de Hall. Por lo tanto, esta importante relación lleva el nombre de Hall y Petch.

Relación Hall-Petch inversa

La relación de Hall-Petch predice que a medida que disminuye el tamaño de grano, aumenta el límite elástico. Se encontró experimentalmente que la relación de Hall-Petch es un modelo efectivo para materiales con tamaños de grano que van desde 1 milímetro hasta 1 micrómetro. En consecuencia, se creía que si el tamaño de grano medio podía reducirse aún más hasta la escala de longitud nanométrica, el límite elástico también aumentaría. Sin embargo, los experimentos en muchos materiales nanocristalinos demostraron que si los granos alcanzaran un tamaño lo suficientemente pequeño, el tamaño de grano crítico que normalmente es de alrededor de 10 nm, el límite elástico permanecería constante o se reduciría al disminuir el tamaño de los granos.[9][10] Este fenómeno se ha denominado relación inversa de Hall-Petch. Se han propuesto varios mecanismos diferentes para explicar esta relación. Como sugirió Carlton et al., se dividen en cuatro categorías: (1) basadas en dislocaciones, (2) basadas en difusión, (3) basadas en cizallamiento del límite de grano, (4) basadas en dos fases.[11]

Se han realizado varios trabajos para investigar el mecanismo detrás de la relación inversa de Hall-Petch en numerosos materiales. En el trabajo de Han,[12] se realizó una serie de simulaciones de dinámica molecular para investigar el efecto del tamaño de grano en las propiedades mecánicas del grafeno nanocristalino bajo carga de tracción uniaxial, con formas aleatorias y orientaciones aleatorias de los anillos de grafeno. La simulación se realizó con tamaños de grano de nm y a temperatura ambiente. Se encontró que en el tamaño de grano del rango de 3,1 nm a 40 nm, se observó una relación inversa de Hall-Petch. Esto se debe a que cuando el tamaño de grano disminuye a escala de nanómetros, hay un aumento en la densidad de las uniones de límite de grano que sirve como fuente de crecimiento de grietas o de unión débil. Sin embargo, también se observó que a un tamaño de grano por debajo de 3,1 nm, se presenta una pseudo relación de Hall-Petch, lo que da como resultado un aumento en la resistencia. Esto se debe a una disminución en la concentración de tensión de las uniones del límite de grano y también a la distribución de tensión de 5-7 defectos en el límite de grano donde los anillos del pentágono y heptágono producen la tensión de compresión y tracción, etc. Chen et al.[13] han investigado las relaciones de Hall-Petch inversas de las aleaciones CoNiFeAl_xCu_1–x de alta entropía. En el trabajo, se construyeron modelos policristalinos de CoNiFeAl_0.3Cu_0.7 estructurados por FCC con tamaños de grano que oscilan entre 7,2 nm y 18,8 nm para realizar una compresión uniaxial mediante simulaciones de dinámica molecular. Todas las simulaciones de compresión se realizaron después de establecer las condiciones de contorno periódicas en las tres direcciones ortogonales. Se encontró que cuando el tamaño de grano está por debajo de 12,1 nm se observa la relación inversa de Hall-Petch. Esto se debe a que a medida que disminuye el tamaño de grano, las dislocaciones parciales se vuelven menos prominentes y, por lo tanto, la macla por deformación. En cambio, se observó que hay un cambio en la orientación de los granos y la migración de los límites de los granos y, por lo tanto, provoca el crecimiento y la contracción de los granos vecinos. Estos son los mecanismos de las relaciones inversas de Hall-Petch. Sheinermann et al.[14] también estudiaron la relación inversa de Hall-Petch para cerámicas nanocristalinas. Se encontró que el tamaño de grano crítico para la transición de la relación de Hall-Petch directa a la relación de Hall-Petch inversa depende fundamentalmente de la energía de activación del deslizamiento del límite de grano. Esto se debe a que en la relación de Hall-Petch directa, el mecanismo de deformación dominante es el movimiento de dislocación intragrano, mientras que en la relación de Hall-Petch inversa, el mecanismo dominante es el deslizamiento del límite de grano. Se concluyó que al representar tanto la fracción de volumen del deslizamiento del límite de grano como la fracción de volumen del movimiento de dislocación intragrano en función del tamaño de grano, el tamaño de grano crítico se puede encontrar donde se cruzan las dos curvas.

Otras explicaciones que se han propuesto para racionalizar el aparente ablandamiento de los metales con granos de tamaño nanométrico incluyen la mala calidad de la muestra y la supresión de las acumulaciones de dislocaciones.[15]

La acumulación de dislocaciones en los límites de grano es un mecanismo característico de la relación de Hall-Petch. Sin embargo, una vez que los tamaños de grano caen por debajo de la distancia de equilibrio entre las dislocaciones, esta relación ya no debería ser válida. Sin embargo, no está del todo claro cuál debería ser exactamente la dependencia del límite elástico con respecto a los tamaños de grano por debajo de este punto.

Refinamiento del grano

Inoculantes típicos para varias aleaciones fundidas[16]
Metal	Inoculante
Acero moldeado	FeSi, SiCa, grafito
Aleaciones de Mg	Zr, C
Aleaciones de Cu	Fe, Co, Zr
Aleaciones de Al–Si	P, Ti, B, Sc
Aleaciones de Pb	As, Te
Aleaciones de Zn	Ti
Aleaciones de Ti	Al–Ti intermetálicos

El refinamiento del grano, también conocido como inoculación,[16] es el conjunto de técnicas utilizadas para incrementar el fortalecimiento del límite de grano en metalurgia. Las técnicas específicas y los mecanismos correspondientes variarán según los materiales que se estén considerando.

Un método para controlar el tamaño de grano en las aleaciones de aluminio es mediante la introducción de partículas que sirvan como nucleantes, como Al–5%Ti. Los granos crecerán a través de nucleación heterogénea; es decir, para un grado dado de subenfriamiento por debajo de la temperatura de fusión, las partículas de aluminio en la masa fundida se nuclearán en la superficie de las partículas añadidas. Los granos crecerán en forma dendrítica creciendo radialmente alejándose de la superficie del nucleante. Luego se pueden agregar partículas de soluto (llamadas refinadoras de granos) que limitan el crecimiento de las dendritas, lo que lleva a la refinación de granos. Las aleaciones[17] Al-Ti-B son los refinadores de grano más comunes para las aleaciones de aluminio; sin embargo,[18] se han sugerido refinadores novedosos como Al₃Sc.

Una técnica común es inducir a una fracción muy pequeña de la masa fundida a solidificarse a una temperatura mucho más alta que el resto; esto generará cristales semilla que actuarán como plantilla cuando el resto del material baje hasta su punto de fusión (inferior) y comience a solidificarse. Dado que está presente una gran cantidad de minúsculos cristales semilla, resulta una cantidad casi igual de cristalitos, y el tamaño de cualquier grano es limitado.

Véase también

Mecanismos de endurecimiento de los materiales

Referencias

W.D. Callister. Fundamentals of Materials Science and Engineering, 2nd ed. Wiley & Sons. pp. 252.
Schuh, Christopher; Nieh, T.G. (2003), «Hardness and Abrasion Resistance of Nanocrystalline Nickel Alloys Near the Hall–Petch Breakdown Regime», Mater. Res. Soc. Symp. Proc. 740, doi:10.1557/proc-740-i1.8..
«Answers - the Most Trusted Place for Answering Life's Questions».
Lesuer, D.R; Syn, C.K; Sherby, O.D (2007), «Nano-subgrain strengthening in ball-milled iron», Materials Science and Engineering: A 463 (1–2): 54-60, doi:10.1016/j.msea.2006.07.161.
Smith y Hashemi, 2006, p. 243.
Smith y Hashemi, 2006, p. 242.
Hall, E.O. (1951). «The Deformation and Ageing of Mild Steel: III Discussion of Results». Proc. Phys. Soc. Lond. 64 (9): 747-753. Bibcode:1951PPSB...64..747H. doi:10.1088/0370-1301/64/9/303.
Petch, N.J. (1953). «The Cleavage Strength of Polycrystals». J. Iron Steel Inst. London 173: 25-28.
Conrad, H; Narayan, J (2000). «On the grain size softening in nanocrystalline materials». Scripta Mater 42 (11): 1025-30. doi:10.1016/s1359-6462(00)00320-1.
Park, H; Rudd, R; Cavallo, R; Barton, N; Arsenlis, A; Belof, J; Blobaum, K; El-dasher, B; Florando, J; Huntington, C; Maddox, B; May, M; Plechaty, C; Prisbrey, S; Remington, B; Wallace, R; Wehrenberg, C; Wilson, M; Comley, A; Giraldez, E; Nikroo, A; Farrell, M; Randall, G; Gray, G (2015). «Grain-Size-Independent Plastic Flow at Ultrahigh Pressures and Strain Rates». Phys. Rev. Lett. 114 (6): 065502. Bibcode:2015PhRvL.114f5502P. PMID 25723227. doi:10.1103/PhysRevLett.114.065502.
Carlton, C; Ferreira, P. J. (2007). «What is Behind the Inverse Hall–Petch Behavior in Nanocrystalline Materials?.». Mater. Res. Soc. Symp. Proc. 976.
Han, Jihoon. "The transition from an inverse pseudo Hall–Petch to a pseudo Hall–Petch behavior in nanocrystalline graphene." Carbon 161 (2020): 542-549
Chen, Shuai, et al. "Hall-Petch and inverse Hall-Petch relations in high-entropy CoNiFeAlxCu1-x alloys." Materials Science and Engineering: A 773 (2020): 138873
Sheinerman, Alexander G., Ricardo HR Castro, and Mikhail Yu Gutkin. "A model for direct and inverse Hall-Petch relation for nanocrystalline ceramics." Materials Letters 260 (2020): 126886
Schiotz, J.; Di Tolla, F.D.; Jacobsen, K.W. (1998). «Softening of nanocrystalline metals at very small grains». Nature 391 (6667): 561. S2CID 4411166. doi:10.1038/35328.
Stefanescu, Doru Michael (2002), Science and engineering of casting solidification, Springer, p. 265, ISBN 978-0-306-46750-9.
K.T. Kashyap and T. Chandrashekar, "Effects and mechanisms of grain refinement in aluminum alloys," Bulletin of Materials Science, vol 24, August 2001
Fan, Z.; Wang, Y.; Zhang, Y.; Qin, T.; Zhou, X.R.; Thompson, G.E.; Pennycook, T.; Hashimoto, T. (2015). «Grain refining mechanism in the Al/Al–Ti–B system». Acta Materialia 84: 292-304. doi:10.1016/j.actamat.2014.10.055.

Bibliografía

Smith, William F.; Hashemi, Javad (2006), Foundations of Materials Science and Engineering (4th edición), McGraw-Hill, ISBN 978-0-07-295358-9..

Enlaces externos

Datos: Q264845
Multimedia: Grain boundary strengthening / Q264845

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[Callister-1] W.D. Callister. Fundamentals of Materials Science and Engineering, 2nd ed. Wiley & Sons. pp. 252.

[Grain_boundary_sliding-2] Schuh, Christopher; Nieh, T.G. (2003), «Hardness and Abrasion Resistance of Nanocrystalline Nickel Alloys Near the Hall–Petch Breakdown Regime», Mater. Res. Soc. Symp. Proc. 740, doi:10.1557/proc-740-i1.8..

[3] «Answers - the Most Trusted Place for Answering Life's Questions».

[4] Lesuer, D.R; Syn, C.K; Sherby, O.D (2007), «Nano-subgrain strengthening in ball-milled iron», Materials Science and Engineering: A 463 (1–2): 54-60, doi:10.1016/j.msea.2006.07.161.

[5] Smith y Hashemi, 2006, p. 243.

[6] Smith y Hashemi, 2006, p. 242.

[7] Hall, E.O. (1951). «The Deformation and Ageing of Mild Steel: III Discussion of Results». Proc. Phys. Soc. Lond. 64 (9): 747-753. Bibcode:1951PPSB...64..747H. doi:10.1088/0370-1301/64/9/303.

[8] Petch, N.J. (1953). «The Cleavage Strength of Polycrystals». J. Iron Steel Inst. London 173: 25-28.

[Conrad-9] Conrad, H; Narayan, J (2000). «On the grain size softening in nanocrystalline materials». Scripta Mater 42 (11): 1025-30. doi:10.1016/s1359-6462(00)00320-1.

[Park-10] Park, H; Rudd, R; Cavallo, R; Barton, N; Arsenlis, A; Belof, J; Blobaum, K; El-dasher, B; Florando, J; Huntington, C; Maddox, B; May, M; Plechaty, C; Prisbrey, S; Remington, B; Wallace, R; Wehrenberg, C; Wilson, M; Comley, A; Giraldez, E; Nikroo, A; Farrell, M; Randall, G; Gray, G (2015). «Grain-Size-Independent Plastic Flow at Ultrahigh Pressures and Strain Rates». Phys. Rev. Lett. 114 (6): 065502. Bibcode:2015PhRvL.114f5502P. PMID 25723227. doi:10.1103/PhysRevLett.114.065502.

[Carlton-11] Carlton, C; Ferreira, P. J. (2007). «What is Behind the Inverse Hall–Petch Behavior in Nanocrystalline Materials?.». Mater. Res. Soc. Symp. Proc. 976.

[12] Han, Jihoon. "The transition from an inverse pseudo Hall–Petch to a pseudo Hall–Petch behavior in nanocrystalline graphene." Carbon 161 (2020): 542-549

[13] Chen, Shuai, et al. "Hall-Petch and inverse Hall-Petch relations in high-entropy CoNiFeAlxCu1-x alloys." Materials Science and Engineering: A 773 (2020): 138873

[14] Sheinerman, Alexander G., Ricardo HR Castro, and Mikhail Yu Gutkin. "A model for direct and inverse Hall-Petch relation for nanocrystalline ceramics." Materials Letters 260 (2020): 126886

[Schiotz2-15] Schiotz, J.; Di Tolla, F.D.; Jacobsen, K.W. (1998). «Softening of nanocrystalline metals at very small grains». Nature 391 (6667): 561. S2CID 4411166. doi:10.1038/35328.

[stefanescu-16] Stefanescu, Doru Michael (2002), Science and engineering of casting solidification, Springer, p. 265, ISBN 978-0-306-46750-9.

[17] K.T. Kashyap and T. Chandrashekar, "Effects and mechanisms of grain refinement in aluminum alloys," Bulletin of Materials Science, vol 24, August 2001

[18] Fan, Z.; Wang, Y.; Zhang, Y.; Qin, T.; Zhou, X.R.; Thompson, G.E.; Pennycook, T.; Hashimoto, T. (2015). «Grain refining mechanism in the Al/Al–Ti–B system». Acta Materialia 84: 292-304. doi:10.1016/j.actamat.2014.10.055.