Estructuras de datos persistentes

El método del nodo gordo consiste en almacenar todos los cambios hechos a propiedades de un nodo de la estructura, en el mismo nodo, si borrar los valores anteriores de sus propiedades. Esto requiere que los nodos puedan ser arbitrariamente “gruesos”. Cada nodo debe permitir guardar cualquier cantidad de campos adicionales. Cada campo adicional tiene una propiedad, un valor y una marca de tiempo que indica la versión en la cual dicha propiedad tomó ese valor. Además cada nodo tiene una marca de tiempo que indica la versión en la que dicho nodo fue creado. El motivo de que los nodos tengan marcas de tiempo es para asegurar que cada nodo tenga un solo valor para cada propiedad para cada versión. Para poder recorrer la estructura, cada campo original tiene cero como marca de tiempo.

Utilizando el método Nodo Grueso, se requiere O(1) de espacio por cada modificación: solo almacenar el nuevo valor. Cada modificación necesita O(1) de tiempo adicional para almacenar el cambio al final de la lista de cambios. Esto es una cota Costo amortizado, asumiendo que guardamos la lista de modificación en un vector (informática) que puede crecer. Para el acceso, debemos encontrar la versión correcta en cada nodo mientras recorremos la estructura. Si hacemos m modificaciones, entonces cada operación de acceso tiene un factor O(log m) que resulta de buscar la modificación más cercana en el historial de modificaciones.

Copia de camino consiste en copiar todos los nodos en el camino desde la raíz del árbol hasta el nodo que vamos actualizar, insertar o borrar. Después hay que actualizar en cascada el cambio: todos los nodos que apuntaban a un nodo viejo deben apuntar al nodo nuevo. Estas modificaciones provocan más cambios en cascada, y así sucesivamente, hasta que lleguemos a la raíz. Se mantiene además una lista de raíces indexadas por marcas de tiempo, de forma tal, que la estructura que tiene como raíz t es exactamente la t-ésima versión.

El costo de modificación temporal y espacial está dado por el tamaño de la estructura, debido a que una modificación puede afectarla completamente. En el caso de los árboles que tengan altura logarítmica, se puede garantizar que el costo de modificación será O(log n) donde n es la cantidad de nodos del árbol, ya que solo cambian los que están en el camino de la raíz al nodo que se va a modificar.

Sleator, Tarjan et al. proponen una combinación que aprovecha las ventajas de los nodos gruesos y de copiar el camino, obteniendo O(1) de costo adicional temporal y O(1) de costo adicional espacial para el acceso y la modificación.

En cada nodo se guarda una campo de modificación. Este campo puede almacenar una modificación de una propiedad del nodo o una modificación de uno de sus punteros, con una marca de tiempo que indica la versión en la que se hizo la modificación. Inicialmente el campo de modificación de cada nodo está vacío.

Cada vez que se accede a un nodo, se chequea el campo de modificación, y se compara la marca de tiempo con la versión que se está accediendo. Si el campo de modificación está vacío, o la versión de acceso es anterior a la marca de tiempo, entonces se ignora el campo de modificación. De lo contrario, si la versión de acceso es posterior a la marca de tiempo, entonces se utiliza el valor que está en el campo de modificación. Por ejemplo, si el campo de modificación tiene un nuevo puntero al hijo izquierdo (en el caso de un árbol binario), entonces se considera que este es el hijo izquierdo del nodo.

Para modificar un nodo (se asume que una modificación cambia un puntero o una propiedad de un nodo), si el campo de modificación del nodo está vacío, lo llenamos con la modificación. De lo contrario, se crea una copia del nodo, pero utilizando solo los últimos valores, o sea sobrescribiendo la propiedad o puntero que se encuentra en el campo de modificación, y se hace la modificación directamente en el nuevo nodo, sin utilizar el campo de modificación, o sea, se sobrescribe la propiedad o el puntero directamente y el campo de modificación se queda vacío. Finalmente se propaga en cascada este cambio al padre del nodo, de la misma forma que se hace en copia del camino. Si el nodo no tiene padre, o sea, es la raíz, y hay que copiarla, se añade en una lista ordenada de raíces.

Con este algoritmo, dado una versión t, a lo sumo un campo de modificación existe con tiempo t. Por lo tanto, una modificación en el tiempo t, divide el árbol en tres partes: una parte contiene los datos antes del tiempo t, otra contiene los datos después del tiempo t, y la otra parte no fue afectada por la modificación.

El costo temporal y espacial requiere un análisis amortizado. Una modificación toma costo espacial amortizado O(1), y costo temporal amortizado O(1). Para demostrarlo, se utiliza una función potencial ϕ, donde ϕ(T) es el número de nodos llenos vivos en T. Los nodos vivos de T, son aquellos que son accesibles desde la raíz actual, en el tiempo actual, o sea, después de la última modificación. Los nodos llenos vivos, son los nodos vivos que tienen algo en su campo de modificación.

Cada modificación conlleva cierto número de copias, digamos k, seguidas de 1 cambio en un campo de modificación. Cada una de las k copias tiene O(1) costo temporal y espacial, pero disminuye la función potencial en uno, debido a que el nodo que se copia debe estar lleno y vivo, por lo tanto contribuye a la función potencial, pero al copiarlo y cambiar el puntero de su padre dejará de estar vivo, y la copia tiene el campo de modificación vacío así que no está llena, por lo tanto se reemplazó un nodo lleno vivo, por uno que no está lleno). El último paso llena un campo de modificación, esto tiene O(1) de costo temporal y aumenta ϕ en uno.

En resumen, el cambio en ϕ es Δϕ = 1 − k, por lo tanto el costo espacial total es O(k +Δϕ) = O(1) y el costo temporal total es O(k +Δϕ +1) = O(1).

Este ejemplo es tomado de Okasaki. Ver las referencias.

La lista enlazada es las estructuras más utilizada en los lenguajes de programación funcionales.

Considere las dos listas:

xs = [0, 1, 2]
ys = [3, 4, 5]

Estas deben ser representadas en memoria de la siguiente forma:

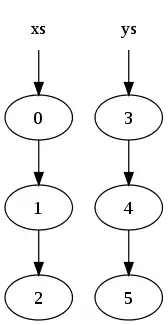
donde un círculo significa un nodo de la lista, y las flechas referencias hacia el nodo que apuntan

Concatenar las dos listas:

zs = xs ++ ys

resulta en la siguiente estructura en memoria:

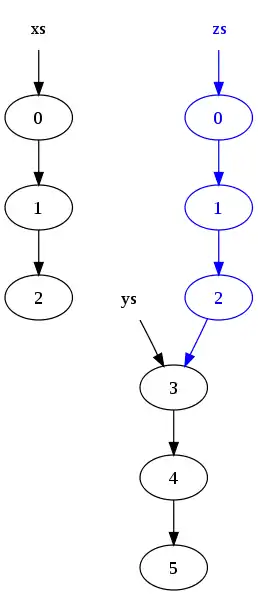
Notar que los nodos en la lista xs han sido copieados, pero los nodos en ys son compartidos. Como resultado, las listas originales (xs y ys) persisten y no han sido modificadas.

La razón de la copia es que el último nodo en xs no puede ser modificado para apuntar el inicio de ys, porque eso cambiaría el valor de xs.

Este ejemplo es tomado de Okasaki. Ver las referencias.

Consideremos un árbol binario utilizado para buscar de forma rápida, donde cada nodo tiene la invariante recursiva de que los valores de los nodos a la izquierda son menores que su valor, y los de la derecha son mayores.

Por ejemplo:

xs = [a, b, c, d, f, g, h]

puede ser representado por el siguiente árbol binario:

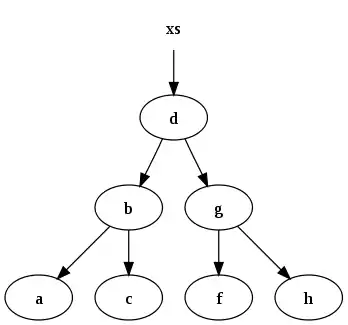
Después de ejecutar de insertar "e" en xs obtenemos lo siguiente:

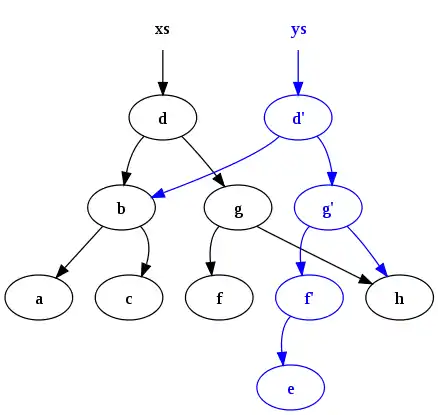
Notemos que el árbol original xs persiste y muchos nodos son compartidos entre ambas versiones. Este tipo de persistencia es muy difícil de manejar sin recolector de basura, para que libere la memoria de los nodos que ya no pueden ser accedidos, es por esto que esta característica es muy común en la programación funcional