Cuantificador existencial
En el lenguaje de predicados en lógica matemática, se usa el símbolo: , llamado cuantificador existencial, antepuesto a una variable para decir que "existe al menos" un elemento del conjunto, , al que hace referencia la variable, que cumple la proposición escrita a continuación.[1]
Existe x que pertenece a B.
Ejemplo
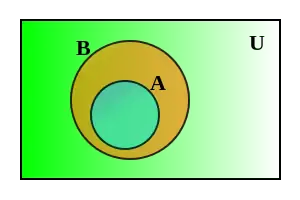
Si tenemos dos conjuntos diferentes y , y es un subconjunto de :
existe al menos un elemento de que pertenece a :
Al afirmar que existe al menos un que pertenece a y pertenece a , quiere decir que no todos los elementos de pertenecen a , al ser y conjuntos distintos, existe al menos un elemento de que no pertenece a :
Que podemos leer: existe al menos un elemento en , y este elemento no pertenece a .
Cuantificador de existencia única
Como relata John F. Sowa[2] (p. 475), a partir de la distinción que Bertrand Russell y Alfred North Whitehead hicieron en los Principia Mathematica en dos operadores, E! «indicando exactamente uno» y E!! indicando «único», Stephen Kleene, definió el cuantificador existencial «exactamente uno» , explícitamente:
- .
y el propio Sowa, el cuantificador existencial «único» , implícitamente:
- .
Hay que notar que en la literatura está muy extendida la denominación «cuantificador de existencia única» para el primero —aunque se mantiene también sobre todo en la literatura inglesa la denominación Kleene's exactly-one quantifier (basta con hacer una búsqueda en Internet)—, y todo ello a pesar de la confusión que esto puede generar, pues no es precisamente lo mismo «exactamente uno» que «único», como argumenta Sowa. Veámoslo con un ejemplo —adaptado de Sowa (p. 475):
- «Exactamente uno»: «Toda persona tiene exactamente una madre». (Dos personas distintas pueden tener la misma madre, dicho de otra forma, la correspondencia de Personas a Personas que son madres no es inyectiva).
- Denotando por el conjunto de las personas, por el conjunto de las personas que son madres y por el predicado « es madre de », o bien, «la madre de es », entonces quedaría formalizado así: .
- Obsérvese que en este ejemplo la unicidad se refiere a la madre, de ahí que pueda leerse perfectamente como: «Toda persona tiene una única madre», sin embargo no queda explícito que personas distintas puedan ser hijas de la misma madre.
- «Único»: «Toda persona tiene un único número de identidad estatal asociado (por ejemplo, en España, un número de DNI)». (Dos personas distintas no tienen el mismo número, en otras palabras, la correspondencia de Personas a Números es inyectiva).
- Denotando por el conjunto de las personas, por el conjunto de números y por el predicado « tiene el número de identidad », entonces quedaría formalizado así: .
- Obsérvese que en este ejemplo la unicidad se refiere a ambos, las personas y los números, quedando explícito que personas distintas no pueden tener números distintos.
Si no se especifica nada en contra, al referirse al cuantificador de existencia única se entiende el primero.
Véase también
Referencias
- Real Academia de Ciencias Exactas, Física y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espsa. ISBN 84-239-7921-0.
- 2000. Knowledge representation : logical, philosophical, and computational foundations, Brooks Cole Publishing Co., Pacific Grove. (Knowledge Representation: Logical, Philosophical, and Computational Foundations at jfsowa.com. Retrieved Nov 23, 2012).