Fórmula de la difracción de Kirchhoff

La fórmula de la difracción de Kirchhoff[1][2] (también conocida como fórmula de la difracción de Fresnel-Kirchhoff) se puede usar para modelizar el fenómeno de la propagación de la luz en una amplia gama de configuraciones, ya sea analíticamente o usando modelos numéricos. Proporciona una expresión para la perturbación de una onda cuando una onda esférica monocroma pasa a través de una abertura en una pantalla opaca. La ecuación se deduce mediante varias aproximaciones al teorema integral de Kirchhoff que se vale del teorema de Green para calcular la solución de la ecuación de onda homogénea.

Deducción de la fórmula de difracción de Kirchhoff

El teorema integral de Kirchhoff, a veces denominado teorema integral de Fresnel-Kirchhoff,[3] utiliza las identidades de Green para deducir la solución de la ecuación de onda homogénea en un punto arbitrario P en términos de los valores de la solución de la ecuación de onda y su derivada de primer orden en todos los puntos de una superficie arbitraria que rodea por completo al punto P.

La solución proporcionada por el teorema integral para una fuente monocroma es:

$U(P)={\frac {1}{4\pi }}\int _{S}\left[U{\frac {\partial }{\partial n}}\left({\frac {e^{iks}}{s}}\right)-{\frac {e^{iks}}{s}}{\frac {\partial U}{\partial n}}\right]dS$
Símbolo	Nombre
$U$	Fasor de la perturbación en la superficie
$k$	Número de onda
$s$	Distancia desde P a la superficie

Las suposiciones hechas son:

U y ∂U/∂n son discontinuos en los límites de la abertura,
La distancia a la fuente puntual y la dimensión de la abertura S son mucho mayores que λ.

Fuente puntual

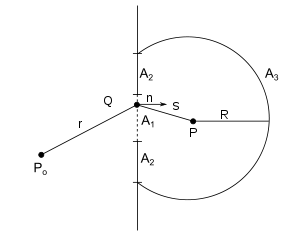
Esquema geométrico usado en la deducción de la fórmula de la difracción de Kirchhhoff

Considérese una fuente puntual monocromática en P₀, que ilumina una abertura en una pantalla. La energía de la onda emitida por una fuente puntual decae en función del inverso del cuadrado de la distancia recorrida, por lo que la amplitud disminuye como el inverso de la distancia. La amplitud compleja de la perturbación a una distancia r viene dada por

$U(r)={\frac {ae^{ikr}}{r}}$
Símbolo	Nombre
$a$	Magnitud de la perturbación en la fuente puntual

La perturbación en un punto P se puede determinar aplicando el teorema integral a la superficie cerrada formada por la intersección de una esfera de radio R con la pantalla. La integración se realiza en las áreas A₁, A₂ y A₃, resultando

$U(P)={\frac {1}{4\pi }}\left[\int _{A_{1}}+\int _{A_{2}}+\int _{A_{3}}\left(U{\frac {\partial }{\partial n}}\left({\frac {e^{iks}}{s}}\right)-{\frac {e^{iks}}{s}}{\frac {\partial U}{\partial n}}\right)\right]dS.$

Para resolver la ecuación, se supone que los valores de U y ∂U/∂n en el área A₁ son los mismos que cuando la pantalla no está presente, dando en Q:

$U_{A_{1}}={\frac {ae^{ikr}}{r}},$ ${\frac {\partial U_{A_{1}}}{\partial n}}={\frac {ae^{ikr}}{r}}\left[ik-{\frac {1}{r}}\right]\cos(n,r)$


Símbolo	Nombre
$r$	Longitud P₀Q
$(n,r)$	Ángulo entre P₀Q y la normal a la abertura

Kirchhoff supone que los valores de U y ∂U/∂n en A₂ son cero. Esto implica que U y ∂U/∂n son discontinuos en el borde de la abertura. Este no es el caso, y esta es una de las aproximaciones usadas para deducirar la ecuación. Estas suposiciones a veces se conocen como las condiciones de contorno de Kirchhoff.

La contribución de A₃ a la integral también se supone que es cero. Esto puede justificarse suponiendo que la fuente comienza a irradiar en un momento determinado y luego haciendo que "R" sea lo suficientemente grande, de modo que cuando se considere la perturbación en P, la aportación de A₃ ya habrá llegado allí.[1] Tal onda ya no es monocroma, y aunque se presupone que una onda monocromática debe existir en todo momento, esta condición no es estrictamente necesaria, y se ha deducido un argumento más formal para evitar su uso.[4]

Se tiene que

${\frac {\partial }{\partial n}}\left({\frac {e^{iks}}{s}}\right)={\frac {e^{iks}}{s}}\left[ik-{\frac {1}{s}}\right]\cos(n,s)$
Símbolo	Nombre
$(n,s)$	Ángulo entre la normal a la abertura y PQ

Finalmente, los términos 1/r y 1/s se consideran insignificantes en comparación con k, ya que r y s son generalmente mucho más grandes que 2π/k, que es igual al longitud de onda. Por lo tanto, la integral anterior, que representa la amplitud compleja en P, se convierte en

U(P)=-{\frac {ia}{2\lambda }}\int _{S}{\frac {e^{ik(r+s)}}{rs}}[\cos(n,r)-\cos(n,s)]\,dS.

Esta es la fórmula de la difracción de Kirchhoff o de Fresnel y Kirchhoff.

Equivalencia con la ecuación de Huygens-Fresnel

Esquema geométrico para expresar la fórmula de Kirchhoff en una forma similar a la de Huygens–Fresnel

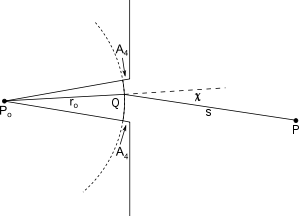
El Principio de Fresnel - Huygens puede deducirse integrando sobre una superficie cerrada diferente. El área A₁ anterior se reemplaza por un frente de onda desde P₀, que casi llena la abertura, y una porción de un cono con un vértice en P₀, que está etiquetada como A₄ en el diagrama. Si el radio de curvatura de la onda es lo suficientemente grande, puede despreciarse la contribución de A₄. También se tiene que

\chi =\pi -(r_{0},s),

donde χ se ajusta a su definición según el Principio de Fresnel - Huygens, y cos (n, r) = 1. La amplitud compleja del frente de onda en r₀ viene dada por

$U(r_{0})={\frac {ae^{ikr_{0}}}{r_{0}}}.$

La fórmula de difracción se convierte en

$U(P)=-{\frac {i}{2\lambda }}{\frac {ae^{ikr_{0}}}{r_{0}}}\int _{S}{\frac {e^{iks}}{s}}(1+\cos \chi )\,dS.$

Esta es la fórmula de difracción de Kirchhoff, que contiene parámetros que deben asignarse arbitrariamente en la deducción de la ecuación de Huygens–Fresnel.

Fuente extensa

Supóngase que la abertura está iluminada por una fuente de ondas extensa.[5] La amplitud en la abertura según su expresión compleja viene dada por U₀(r).

Se supone, como antes, que los valores de U y ∂U/∂n en el área A₁ son los mismos que cuando la pantalla no está presente, que los valores de U y ∂U/∂n en A₂ son cero (condiciones de contorno de Kirchhoff) y que la contribución de A₃ a la integral también es cero. Así mismo, se supone que 1/s es insignificante en comparación con k. Entonces se tiene que

$U(P)=-{\frac {1}{4\pi }}\int _{A_{1}}{\frac {e^{iks}}{s}}\left[ikU_{0}(r)\cos(n,s)-{\frac {\partial U_{0}(r)}{\partial n}}\right]\,dS.$

Esta es la forma más general de la fórmula de difracción de Kirchhoff. Para resolver esta ecuación con una fuente extendida, se requeriría una integración adicional para sumar las contribuciones hechas por los puntos individuales en la fuente. Sin embargo, si se supone que la luz de la fuente en cada punto de la abertura tiene una dirección bien definida, que es el caso si la distancia entre la fuente y la abertura es significativamente mayor que la longitud de onda, entonces se puede escribir

$U_{0}(r)\approx a(r)e^{ikr},$

donde a(r) es la magnitud de la perturbación en el punto r en la abertura. Entonces se tiene

${\frac {\partial {U_{0}(r)}}{\partial n}}=ika(r)\cos(n,r)$

y por lo tanto

$U(P)=-{\frac {i}{2\lambda }}\int _{S}a(r){\frac {e^{iks}}{s}}[\cos(n,s)-\cos(n,r)]\,dS.$

Ecuaciones de la difracción de Fraunhofer y Fresnel

A pesar de las diversas aproximaciones que se hicieron para llegar a la fórmula, es adecuada para describir la mayoría de los problemas de la óptica instrumental. Esto se debe principalmente a que la longitud de onda de la luz es mucho más pequeña que las dimensiones de cualquier obstáculo encontrado. Las soluciones analíticas no son posibles para la mayoría de las configuraciones, pero la ecuación de la difracción de Fresnel y la ecuación de la difracción de Fraunhofer, que son aproximaciones de la fórmula de Kirchhoff para campos próximos y campos lejanos, se pueden aplicar a una amplia gama de sistemas ópticos.

Una de las suposiciones importantes hechas para llegar a la fórmula de la difracción de Kirchhoff es que r y s son significativamente mayores que λ. Se puede hacer una aproximación más, lo que simplifica aún más la ecuación: las distancias P₀Q y QP son mucho mayores que las dimensiones de la abertura. Esto permite hacer dos aproximaciones adicionales:

cos (n, r) - cos (n, s) se reemplaza por 2cos β, donde β es el ángulo entre P₀P y la normal a la abertura. El factor 1/rs se reemplaza por 1/r's', donde r' y s' son las distancias desde P₀ y P al origen, que se encuentra en la abertura. La amplitud compleja se convierte en:

U(P)=-{\frac {ia\cos \beta }{\lambda r's'}}\int _{S}e^{ik(r+s)}\,ds.

Suponiendo que la abertura se encuentra en el plano xy, y las coordenadas de P₀, P y Q (un punto general en la abertura ) son (x₀, y₀, z₀), (x, y, z) y (x', y', 0) respectivamente. Entonces se tiene que:

~r^{2}=(x_{0}-x')^{2}+(y_{0}-y')^{2}+z_{0}^{2},

~s^{2}=(x-x')^{2}+(y-y')^{2}+z^{2},

~r'^{2}=x_{0}^{2}+y_{0}^{2}+z_{0}^{2},

~s'^{2}=x^{2}+y^{2}+z^{2}.

Se pueden expresar r y s de la siguiente manera:

r=r'\left[1-{\frac {2(x_{0}x'+y_{0}y')}{r'^{2}}}+{\frac {x'^{2}+y'^{2}}{r'^{2}}}\right]^{1/2},

s=s'\left[1-{\frac {2(xx'+yy')}{s'^{2}}}+{\frac {x'^{2}+y'^{2}}{s'^{2}}}\right]^{1/2}.

que pueden expandirse como series de potencias:

r=r'\left[1-{\frac {1}{2r'^{2}}}[2(x_{0}x'+y_{0}y')+(x'^{2}+y'^{2})]+{\frac {1}{2r'^{2}}}[2(x_{0}x'+y_{0}y')+(x'^{2}+y'^{2})]^{2}+\cdots \right],

s=s'\left[1-{\frac {1}{2s'^{2}}}[2(xx'+yy')+(x'^{2}+y'^{2})]+{\frac {1}{2s'^{2}}}[2(xx'+yy')+(x'^{2}+y'^{2})]^{2}+\cdots \right].

La amplitud compleja en P ahora se puede expresar como

U(P)=-{\frac {i\cos \beta }{\lambda }}{\frac {ae^{ik(r'+s')}}{r's'}}\int _{S}e^{ikf(x',y')}\,dx'dy',

donde f( x', y') incluye todos los términos en las expresiones anteriores para s y r aparte del primer término en cada expresión y puede escribirse en la forma

f(x',y')=c_{1}x'+c_{2}y'+c_{3}x'^{2}+c_{4}y'^{2}+c_{5}x'y'\cdots ,

donde los términos c_i son constantes.

Difracción de Fraunhofer

Si se pueden despreciar todos los términos en f(x', y') a excepción de los términos en x' e y', se tiene la ecuación de la difracción de Fraunhofer. Si los cosenos de dirección de P₀Q y PQ son

{\begin{aligned}l_{0}&=-x_{0}/r',\\m_{0}&=-y_{0}/r',\\l&=x/s',\\m&=y/s'.\end{aligned}}

La ecuación de la difracción de Fraunhofer es entonces

U(P)=C\int _{S}e^{ik[(l_{0}-l)x'+(m-m_{0})y']}\,dx'dy',

donde C es una constante. Esto también se puede escribir en la forma

U(P)=C\int _{S}e^{i(\mathbf {k} _{0}-\mathbf {k} )\cdot \mathbf {r} '}\,dr',

donde k ₀ y k son los vectores de onda de las ondas que viajan de P₀ a la abertura y de la abertura a P respectivamente, y r' es un punto en la abertura.

Si la fuente puntual es reemplazada por una fuente extensa cuya amplitud compleja en la abertura viene dada por U₀(r'), entonces la ecuación de la difracción de Fraunhofer es:

U(P)\propto \int _{S}a_{0}(\mathbf {r} ')e^{i(\mathbf {k} _{0}-\mathbf {k} )\cdot \mathbf {r} '}\,dr',

donde a₀(r') es, como antes, la magnitud de la perturbación en la abertura.

Además de las aproximaciones realizadas en la deducción de la ecuación de Kirchhoff, se supone que

r y s son significativamente mayores que el tamaño de la abertura,
Los términos de segundo orden y de orden superior en la expresión f (x', y') pueden despreciarse.

Difracción de Fresnel

Cuando los términos cuadráticos no se pueden despreciar, pero sí todos los términos de orden superior, la ecuación se convierte en la ecuación de la difracción de Fresnel. Se usan las aproximaciones para la ecuación de Kirchhoff, y las suposiciones adicionales son:

r y s son significativamente mayores que el tamaño de la abertura,
Los términos de tercer y mayor orden en la expresión f ( x', y') pueden ser ignorados.

Referencias

Born, Max; Wolf, Emil (1999). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. Cambridge: Cambridge University Press. p. 986. ISBN 9780521642224.
Longhurst, Richard Samuel (1986). Geometrical And Physical Optics. Orient BlackSwan. p. 651. ISBN 8125016236.
Kirchhoff, G. (1883). «Zur Theorie der Lichtstrahlen». Annalen der Physik (en alemán) (Wiley) 254 (4): 663-695. Bibcode:1882AnP...254..663K. doi:10.1002/andp.18832540409.
M. Born, Optik: ein Lehrbuch der elektromagnetischen Lichttheorie. Berlin, Springer, 1933, reprinted 1965, p. 149.
M. V. Klein & T. E. Furtak, 1986, Optics; 2nd ed. John Wiley & Sons, New York ISBN 0-471-87297-0.

Lecturas adicionales

Woan, Graham (2000). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 9780521575072.
Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson Education, Limited. ISBN 978-0-321-85656-2.
Band, Yehuda B. (2006). Light and Matter: Electromagnetism, Optics, Spectroscopy and Lasers. John Wiley & Sons. ISBN 978-0-471-89931-0.
Kenyon, Ian (2008). The Light Fantastic: A Modern Introduction to Classical and Quantum Optics. Oxford University Press. ISBN 978-0-19-856646-5.
Lerner, Rita G.; George L., Trigg (1991). Encyclopedia of physics. VCH. ISBN 978-0-89573-752-6.
Sybil P., Parker (1993). MacGraw-Hill Encyclopedia of Physics. McGraw-Hill Ryerson, Limited. ISBN 978-0-07-051400-3.

Datos: Q7408338

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[Born_and_Wolf-1] Born, Max; Wolf, Emil (1999). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. Cambridge: Cambridge University Press. p. 986. ISBN 9780521642224.

[2] Longhurst, Richard Samuel (1986). Geometrical And Physical Optics. Orient BlackSwan. p. 651. ISBN 8125016236.

[3] Kirchhoff, G. (1883). «Zur Theorie der Lichtstrahlen». Annalen der Physik (en alemán) (Wiley) 254 (4): 663-695. Bibcode:1882AnP...254..663K. doi:10.1002/andp.18832540409.

[4] M. Born, Optik: ein Lehrbuch der elektromagnetischen Lichttheorie. Berlin, Springer, 1933, reprinted 1965, p. 149.

[5] M. V. Klein & T. E. Furtak, 1986, Optics; 2nd ed. John Wiley & Sons, New York ISBN 0-471-87297-0.