Fórmula del área de Gauss
La Fórmula del área de Gauss, Fórmula de la Lazada o Algoritmo de la Lazada, es un algoritmo matemático usado para calcular el área de un polígono simple cuyos vértices están descritos como pares de coordenadas en el plano.[1] [2]
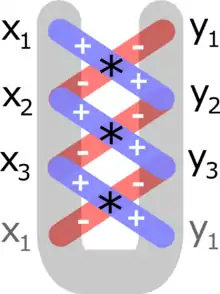
Es conocido como fórmula de la lazada debido al constante cruce de productos de las correspondientes coordenadas de cada par de vértices, similar al atar una lazada.[1] También recibe el nombre de Fórmula del área de Gauss en honor a Carl Friedrich Gauss. Tiene múltiples aplicaciones en agrimensura e ingeniería de montes entre otras áreas.[3][4]
Formulación
La fórmula puede representarse mediante la expresión:
donde
- A es el área del polígono,
- n es el número de lados del polígono, y
- (xi, yi), i = 1, 2,..., n son los vértices del polígono.
de forma alternativa:[3][5][6]
donde, al tratarse de un polígono cíclico xn+1 = x1 y xn = x0, al igual que yn+1 = y1 y yn = y0.
Si los vértices del polígono están listados de forma secuencial con sentido antihorario, entonces cada uno de los determinantes del sumatorio anterior es positivo, y el operador de valor absoluto puede ser omitido;[4] Si los vértices están listados con sentido horario, el determinante será siempre negativo. Esto es debido a que la fórmula puede ser vista como un caso especial del Teorema de Green.
Esta propiedad tiene una importante aplicación en geometría computacional, pues permite analizar el signo de la ecuación anterior para determinar si una secuencia de vértices se encuentra ordenada en sentido horario o antihorario.
Ejemplos
El usuario debe conocer las coordenadas de los vértices del polígono en un plano cartesiano. Por ejemplo, dado el triángulo con coordenadas {(2, 1), (4, 5), (7, 8)}. Tome la primera coordenada x y multiplíquela por la segunda coordenada y, luego tome la segunda coordenada x y multiplíquela por la tercera coordenada y, y repita hasta hacerlo para todos los vértices. Esto puede definirse mediante la siguiente fórmula:[7]
donde xi y yi representan la respectivas coordenadas. Esta fórmula es la expansión de la formulación anterior para el caso n = 3. Uno puede encontrar que el área del triángulo es igual a la mitad del valor absoluto de 10 + 32 + 7 − 4 − 35 − 16, que es igual a 3. El número de variables depende del número de lados del polígono. Por ejemplo, un pentágono definiría coordenadas hasta x5 y y5:
Un ejemplo más complejo
Considere el polígono definido por los vértices (3,4), (5,11), (12,8), (9,5), y (5,6), ilustrado en el siguiente diagrama:
.svg.png.webp)
El área del polígono será:
Explicación del nombre
La razón por la que esta fórmula es llamada fórmula de la lazada es debido a un método común para evaluarla empleando matrices. Por ejemplo, dado el triángulo con vértices (2,4), (3,−8), y (1,2), es posible construir la siguiente matriz apilando las coordenadas y repitiendo el primer vértice al final de la matriz.[8]
Ahora, dibuje diagonales hacia abajo y a la derecha...
y multiplique cada par de números conectados por un trazo, y luego sume todos los productos: (2 × −8) + (3 × 2) + (1 × 4) = −6.
Repita lo mismo con trazos diagonales hacia abajo y la izquierda...
obteniendo (4 × 3) + (−8 × 1) + (2 × 2) = 8.
Finalmente, calcule la diferencia entre ambos números y tome su valor absoluto: |−6 − 8| = 14. Dividiendo entre dos, obtendrá el área del triángulo: 7. Organizar los números de esta forma hace más sencillo recordar y evaluar la fórmula. Tras dibujar todos los trazos, la matriz se asemeja al cordón de una zapatilla.
Referencias
- Dahlke, Karl. «Shoelace Formula». Consultado el 4 de diciembre de 2014.
- Weisstein, Eric W. «Polygon Area». Consultado el 4 de diciembre de 2014.
- Hans Pretzsch, Forest Dynamics, Growth and Yield: From Measurement to Model, Springer, 2009, ISBN 3-540-88306-1, p. 232.
- Bart Braden (1986). «The Surveyor’s Area Formula». The College Mathematics Journal 17 (4): 326-337. doi:10.2307/2686282. Archivado desde el original el 6 de abril de 2015. Consultado el 4 de diciembre de 2014.
- Shoelace Theorem Archivado el 14 de mayo de 2014 en Wayback Machine., Art of Problem Solving Wiki.
- Weisstein, Eric W. «Polygon Area». Wolfram MathWorld. Consultado el 24 de julio de 2012.
- Richard Rhoad; George Milauskas; Robert Whipple (1991). Geometry for Enjoyment and Challenge (new edición). McDougal Littell. pp. 717–718. ISBN 0-86609-965-4.
- IMSA JHMC Guide, Page. 10 "Shoelace" by Cindy Xi