Fórmulas de Newton-Cotes

En análisis numérico las fórmulas de Newton-Cotes (nombradas así por Isaac Newton y Roger Cotes) son un grupo de fórmulas de integración numérica de tipo interpolatorio, en las cuales se evalúa la función en puntos equidistantes, para así hallar un valor aproximado de la integral.

Este método es eficiente si se conocen los valores de la función en puntos igualmente separados. Si se pueden cambiar los puntos en los cuales la función es evaluada otros métodos como la cuadratura de Gauss son probablemente más eficientes.

Introducción

Para la integración numérica de $\int _{a}^{b}f(x)dx$ utilizando las fórmulas de Newton-Cotes se subdivide el intervalo $[a,b]$ en $n$ intervalos iguales. Así se obtienen $n+1$ puntos donde se evaluará la función:

a\leq x_{0}<x_{1}<\ldots <x_{n}\leq b.

Si $a=x_{0}$ y $b=x_{n}$ se denominan fórmulas cerradas de Newton-Cotes ya que los intervalos de los extremos están incluidos en la integral, si por el contrario no se tienen en cuenta se denominan fórmulas abiertas de Newton-Cotes. Para el cálculo se utilizará la siguiente función:

p(x)=\sum _{i=0}^{n}f(x_{i})L_{in}(x)

donde:

L_{in}(x)={\frac {(x-x_{0})\cdots (x-x_{i-1})(x-x_{i+1})\cdots (x-x_{n})}{(x_{i}-x_{0})\cdots (x_{i}-x_{i-1})(x_{i}-x_{i+1})\cdots (x_{i}-x_{n})}}

es el polinomio de Lagrange, por lo tanto se deduce que

\int _{a}^{b}p(x)dx=(b-a)\sum _{i=0}^{n}f(x_{i}){\frac {1}{(b-a)}}\int _{a}^{b}L_{in}(x)dx.

Esta función se expresa de la siguiente forma

\int _{a}^{b}f(x)dx\approx \int _{a}^{b}p(x)dx=(b-a)\sum _{i=0}^{n}w_{i}f(x_{i})

Donde los "pesos" w_i están definidos por

w_{i}={\frac {1}{(b-a)}}\int _{a}^{b}L_{in}(x)dx

Fórmulas cerradas de Newton-Cotes

Estas son algunas de las fórmulas cerradas de Newton-Cotes.

La notación $\displaystyle f_{i}$ es una abreviatura de $\displaystyle f(x_{i})$ , con $\displaystyle x_{i}=a+i\times h$ , $\displaystyle h={\frac {b-a}{n}}$ y $\displaystyle n$ el grado.

Regla del trapecio

Ilustración de la regla del trapecio.

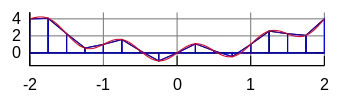
La regla del trapecio consiste en hallar la integral aproximada de una función a través de un polinomio de primer grado, es decir uniendo mediante una recta los puntos en donde se evaluara la función.

\int _{a}^{b}f(x)dx\approx {\frac {h}{2}}(f_{0}+f_{1})

Y el error es:

$-{\frac {h^{3}}{12}}\,f^{(2)}(\xi )$

Siendo $\xi$ un número entre a y b.

Regla de Simpson

Ilustración de la regla de Simpson.

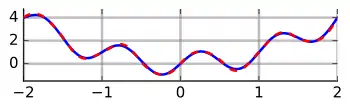
La regla de Simpson (nombrada así por Thomas Simpson) halla la integral aproximada de una función mediante un polinomio de segundo o tercer grado.

Regla de Simpson 1/3

La regla de Simpson 1/3 utiliza tres puntos consecutivos en donde se evalúa la función a través de un polinomio de segundo grado.

\int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}(f_{0}+4f_{1}+f_{2})

Y el error es:

-{\frac {h^{5}}{90}}f^{(4)}(\xi ),

siendo $\xi$ un número entre a y b.

Regla de Simpson 3/8

La regla de Simpson 3/8 utiliza cuatro puntos consecutivos en donde se evalúa la función a través de un polinomio de tercer grado.

\int _{a}^{b}f(x)\,dx\approx {\frac {3h}{8}}(f_{0}+3f_{1}+3f_{2}+f_{3})

.

Y el error es:

-{\frac {3h^{5}}{80}}f^{(4)}(\xi ),

Siendo $\xi$ un número entre a y b.

Regla de Boole

La regla de Boole (llamada así debido a George Boole) utiliza cinco puntos consecutivos igualmente separados para calcular la integral aproximada de la función utilizando un polinomio de cuarto grado.

\int _{a}^{b}f(x)dx\approx {\frac {2h}{45}}(7f_{0}+32f_{1}+12f_{2}+32f_{3}+7f_{4})

Y el error es:

$-{\frac {8h^{7}}{945}}\,f^{(6)}(\xi )$

Siendo $\xi$ un número entre a y b.

Regla de quinto orden

La regla de quinto orden utiliza seis puntos consecutivos igualmente separados para calcular la integral aproximada de la función utilizando un polinomio de quinto grado.

\int _{a}^{b}f(x)dx\approx {\frac {5h}{288}}(19f_{0}+75f_{1}+50f_{2}+50f_{3}+75f_{4}+19f_{5})

Regla de Sexto orden

La regla de sexto orden utiliza siete puntos consecutivos igualmente separados para calcular la integral aproximada de la función utilizando un polinomio de sexto grado.

\int _{a}^{b}f(x)dx\approx {\frac {h}{140}}(41f_{0}+216f_{1}+27f_{2}+272f_{3}+27f_{4}+216f_{5}+41f_{6})

Fórmulas abiertas de Newton-Cotes

Estas son algunas de las fórmulas abiertas de Newton-Cotes.

Regla del punto medio -Integración de Riemann

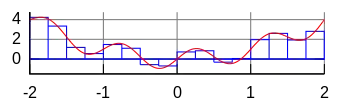
Ilustración de la regla del punto medio.

En este método se divide la función en rectángulos, los cuales deben tener una altura igual al valor de la función en el punto medio. Así se calcularía la integral aproximada mediante un polinomio de grado cero.

\int _{a}^{b}f(x)dx\sim (b-a)f\left({\frac {a+b}{2}}\right)

Y el error es:

{\frac {(b-a)^{3}}{24}}\,f^{(2)}(\xi )

Siendo $\xi$ un número entre a y b.

Reglas compuestas

Las fórmulas de Newton-Cotes aumentan su precisión si se aumenta el número de intervalos en que se divida la función, dicho de otra forma mientras los intervalos sean cada vez más pequeños. Como el intervalo $[a,b]$ generalmente es grande hay métodos que subdividen este intervalo en subintervalos más pequeños y a estos se les aplica las Fórmulas de Newton-Cotes, a la suma de estos subintervalos se le conoce como reglas compuestas. Cabe anotar que la precisión aumenta pero a costa de disminuir la eficiencia del método en cuanto al tiempo de duración y a posibles errores de redondeo.

Regla del trapecio compuesta

Este es un ejemplo de regla compuesta.

\int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left({\frac {f(a)+f(b)}{2}}+\sum _{i=1}^{n-1}f(x_{i})\right)

Donde $\displaystyle x_{i}=a+i\times h$ son los subintervalos,

tal que $\ x_{0}<x_{1}<\ldots <x_{n-1}<x_{n}$ y $\ a=x_{0},\;x_{n}=b$

siendo: $\ h={\frac {b-a}{n}}$ la distancia entre los subintervalos.

Referencias

Programación y Métodos Numéricos: Integración Numérica, Fórmulas de Newton-Cotes, Fórmulas de Gauss. Prof. Carlos Conde Lázaro Prof. Arturo Hidalgo López Prof. Alfredo López. Marzo de 2007. Departamento de Matemática Aplicada y Métodos Informáticos – ETSIM - UPM

Enlaces externos

Datos: Q944241

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.