Galería de litografías (M. C. Escher)
Galería de litografías o Galería de grabados (en neerlandés: Prentententoonstelling) es una litografía impresa en 1956 por el artista holandés M. C. Escher. Representa a un hombre en una galería de arte mirando una litografía de un puerto marítimo, y entre los edificios del puerto marítimo se encuentra la misma galería en la que está parado, haciendo uso del efecto Droste con recursividad visual.[1] La litografía ha suscitado debates tanto en contextos matemáticos como artísticos. Escher consideró que Galería de litografías se encontraba entre sus mejores obras.[2]
Orígenes
Bruno Ernst cita a M. C. Escher diciendo que comenzó Galería de litografías "a partir de la idea de que debe ser posible hacer una protuberancia anular, una expansión cíclica... sin principio ni fin".[3] Escher intentó hacer esto con líneas rectas, pero intuitivamente cambió a líneas curvas que hacen que la cuadrícula se expanda mucho a medida que gira.[3] [4]
Aparente paradoja
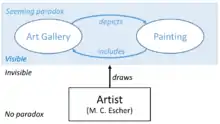
En su libro Gödel, Escher, Bach, Douglas Hofstadter explica la aparente paradoja encarnada en Galería de litografías como un bucle extraño que muestra tres tipos de "adentro": la galería está físicamente en la ciudad ("inclusión"); la ciudad está artísticamente en la imagen ("representación"); la imagen está mentalmente en la persona ("representación").[5]
Posible efecto Droste
La firma de Escher está en un vacío circular en el centro de la obra. En 2003, dos matemáticos holandeses, Bart de Smit y Hendrik Lenstra, informaron sobre una forma de llenar el vacío al tratar el trabajo como dibujado en una curva elíptica sobre el campo de los números complejos. Consideran que una versión idealizada de la obra contiene una copia de sí misma (el efecto Droste), rotada en el sentido de las agujas del reloj unos 157,63 grados y reducida por un factor de unos 22,58.[6] Su sitio web explora aún más la estructura matemática de la imagen.[7]
Posmodernismo
Galería de litografías ha sido discutida en relación con el posmodernismo por varios escritores, incluidos Silvio Gaggi,[8] Barbara Freedman,[9] Stephen Bretzius,[10] y Marie-Laure Ryan.[11]
Referencias
- Merow, Katharine (2013). «Escher and the Droste Effect». Mathematical Association of America. Archivado desde el original el 2 de agosto de 2013.
- Locher, J.L. The Magic of M.C. Escher. Harry N. Abrams, p. 133.
- Ernst, Bruno. De toverspiegel van M. C. Escher, Meulenhoff, Amsterdam, 1976; English translation by John E. Brigham: The Magic Mirror of M. C. Escher, Ballantine Books, Nueva York, 1976
- de Smit, B.; Lenstra, H. W. (2003). «The Mathematical Structure of Escher's Print Gallery». Notices of the American Mathematical Society 50 (4): 446-451.
- Cooper, Jonathan (5 de septiembre de 2007). «Art and Mathematics». Consultado el 5 de septiembre de 2015.
- de Smit, B.; Lenstra, H. W. (2003). «The Mathematical Structure of Escher's Print Gallery». Notices of the American Mathematical Society 50 (4): 446-451. de Smit, B.; Lenstra, H. W. (2003). "The Mathematical Structure of Escher's Print Gallery". Notices of the American Mathematical Society. 50 (4): 446–451.
- Lenstra, Hendrik. «Applying mathematics to Escher's Print Gallery». Leiden University. Archivado desde el original el 6 de junio de 2018. Consultado el 6 de junio de 2018.
- Gaggi, Silvio (1989). Modern/Postmodern: A Study in Twentieth-Century Arts and Ideas. University of Pennsylvania Press. pp. 44-45. ISBN 0-8122-8154-3.
- Freedman, Barbara (1991). Staging the gaze: postmodernism, psychoanalysis, and Shakespearean comedy. Cornell University Press. pp. 124–126. ISBN 0-8014-9737-X.
- Bretzius, Stephen (1997). Shakespeare in theory: the postmodern academy and the early modern theater. University of Michigan Press. p. 57. ISBN 0-472-10853-0.
- Ryan, Marie-Laure (2000). Narrative as virtual reality: immersion and interactivity in literature and electronic media. Johns Hopkins University Press. p. 165. ISBN 0-8018-6487-9.
Enlaces externos
- Escher's Print Gallery Explained.
- Artful Mathematics: The Heritage of M. C. Escher, por Bart de Smit y Hendrik Lenstra.
- Escher's prentententoonstelling (La galería de imágenes de Escher) muestra una animación de las transformaciones matemáticas que involucran un modelo tridimensional de la ciudad y la galería de arte, completo con el código fuente.
- An Animation of Print Gallery creada por Cindy JS.