Gramática (autómata)
Una gramática ("G") desde el punto de vista de la teoría de autómatas es un conjunto finito de reglas que describen toda la secuencia de símbolos pertenecientes a un lenguaje específico L. Dos gramáticas que describan el mismo lenguaje se llaman gramáticas equivalentes.
Una gramática es una estructura algebraica formada por cuatro elementos fundamentales:
G = { NT, T, S, P }
donde
- NT es el conjunto de elementos No Terminales
- T es el conjunto de elementos Terminales
- S es el Símbolo inicial de la gramática
- P es el conjunto de Reglas de Producción
Clasificación de las gramáticas según Padilla
Según Padilla las gramáticas se clasifican de acuerdo a las reglas de sustitución y nunca se pasa autómatas 2:
Tipo 0 o "No restringida o recursivamente enumerables"
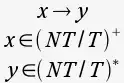
“x puede ser sustituido por y si x está, ya sea, en los símbolos No Terminales o los símbolos Terminales, sin incluir la cadena vacía e y está en los símbolos No Terminales o Terminales, incluyendo la cadena vacía.”
Los lenguajes generados por este tipo de gramáticas se llaman "lenguajes sin restricciones"
Nota: "+" significa "sin incluir la cadena vacía" y "*" significa "incluyendo la cadena vacía". "/" significa "o"
Estos lenguajes también son denominados "recursivamente enumerables"
Las máquinas que los aceptan son las máquinas de Turing (y equivalentes no deterministas)
Tipo 1 o "Sensible al contexto"
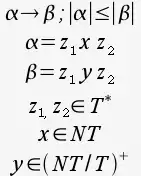
“α puede ser reemplazado por β si la longitud de α es menor o igual a la longitud de β, siendo α un símbolo Terminal o una cadena vacía z1, seguido de un símbolo No Terminal X, seguido de otro símbolo Terminal o una cadena vacía z2. En el caso de β, z1 debe ser el mismo símbolo z1 de α seguido de un símbolo No Terminal o Terminal sin ser la cadena vacía, seguido del símbolo z2.”
Las máquinas que los aceptan son autómatas linealmente acotados(linear-bounded).
Tipo 2 o "libre de contexto"
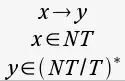
“x puede ser reemplazado por y si x pertenece a los símbolos No Terminales e y es un Terminal o No Terminal, incluyendo la cadena vacía.”
Máquinas que los pueden leer:
Máquinas que los aceptan: Autómata a Pila (Pushdown Automaton)
Tipo 3 o "Regular"
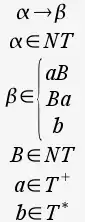
También llamada "De contexto regular"
“α puede ser reemplazado por β si α pertenece a los símbolos No Terminales y β es uno de estos 3:
- Un símbolo Terminal no nulo seguido de un No Terminal.
- Un símbolo No Terminal seguido de un símbolo Terminal no nulo.
- Un símbolo Terminal pudiendo ser la cadena vacía.”
Máquinas que los aceptan: autómata finito, determinista o no determinista.
Véase también
- Otra explicación: Jerarquía de Chomsky.
- Gramática formal.