Gramática ambigua
En Ciencias de la Computación, una gramática ambigua es un Gramática libre del contexto para la que existe una cadena que puede tener más de una derivación a la izquierda, mientras una gramática no ambigua es una Gramática libre del contexto para la que cada cadena válida tiene una única derivación a la izquierda. Muchos lenguajes admiten tanto gramáticas ambiguas como no ambiguas, mientras otros lenguajes admiten solo gramáticas ambiguas. Cualquier lenguaje no vacío admite una gramática ambigua al tomar una gramática no ambigua e introducir una regla duplicada (el único lenguaje sin gramáticas ambiguas es el lenguaje vacío). Un lenguaje que solo admite gramáticas ambiguas se conoce como un Lenguaje Inherentemente Ambiguo, y existen lenguajes libres del contexto inherentemente ambiguos. Las gramáticas libres del contexto deterministas son siempre no-ambiguas, y son una subclase importante de GLCs no-ambiguas; existen GLCs no-deterministas y no-ambiguas simultáneamente.
Ejemplos
Lenguaje trivial
El ejemplo más sencillo es la gramática ambigua siguiente para el lenguaje trivial, que consta sólo de la cadena vacía:
- A → A | ε
…significando que una producción puede ser ella misma otra vez, o la cadena vacía. La cadena vacía tiene derivaciones a la izquierda de longitud 1, 2, 3, y de hecho de cualquier longitud, dependiendo de cuántas veces la regla A → A sea utilizada.
Este lenguaje también tiene la gramática ambigua, que está dada por la siguiente regla:
- A → ε
…significando que con solo esta producción se puede producir la cadena vacía, que es de hecho la única cadena del lenguaje.
De la misma manera, cualquier gramática para un lenguaje no vacío puede ser convertida a ambigua al añadir duplicados.
Cadena unaria
El lenguaje regular de cadenas unarias de un carácter dado, por ejemplo, 'a' (la expresión regular a*), tiene la gramática no-ambigua:
- A → aA | ε
…pero también tiene la gramática ambigua:
- A → aA | Aa | ε
Esto equivale a producir un árbol asociativo a la derecha (para la gramática no-ambigua) o dejando tanto la asociación izquierda como la derecha.
Adición y sustracción
La gramática libre del contexto
- S → S + S | S − S | S * S | id
es ambigua dado que hay dos derivaciones a la izquierda para la cadena a + a + a:
| A | → A + A | A | → A + A | ||
| → a + A | → A + A + A (Primero A es reemplazada por A+A. La sustitución de la segunda A permitiría una derivación similar) | ||||
| → a + A +A | → a + A + A | ||||
| → a + a +A | → a + a + A | ||||
| → a + a + a | → a + a + a |
En el siguiente ejemplo, la gramática es ambigua dado que existen dos árboles de derivación para la cadena a + a − a
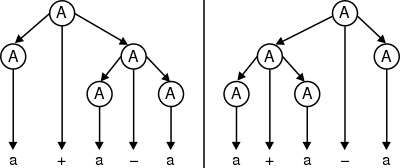
El lenguaje que genera, aun así, no es inherentemente ambiguo; la siguiente es una gramática no-ambigua que genera el mismo lenguaje:
- A → A + a | A − a | a
Reconocimiento de gramáticas ambiguas
El problema de decisión general de si una gramática es ambigua es no decidible y puede ser demostrado que es equivalente al problema de correspondencia de Post.[1] Al menos, existen herramientas que implementan algún procedimiento de decisión para detectar ambigüedad de gramáticas libres del contexto.[2] La eficiencia de una analizador sintáctico de una gramática libre del contexto está determinado por el autómata que la acepta. Las gramáticas libres del contexto deterministas están aceptadas por autómatas con pila deterministas y pueden ser analizadas en tiempo lineal, por ejemplo por el Analizador sintáctico LR.[3] Este es un subconjunto de las gramáticas libres del contexto que son aceptadas por el autómata con pila y pueden ser analizadas en tiempo polinómico, por ejemplo por el algoritmo CYK. Las gramáticas libres del contexto no-ambiguas pueden ser no deterministas. Por ejemplo, el lenguaje de palíndromos de longitud par en el alfabeto de 0 y 1 tiene la gramática libre del contexto no ambigua S → 0S0 | 1S1 | ε. Una cadena arbitraria de este lenguaje no puede ser derivada sin leer todas sus letras primero, lo que significa que un autómata con pila tiene que probar transiciones de estado alternativas para acomodar las diferentes longitudes posibles de un cadena semi-analizada.[4] Eliminar la ambigüedad de una gramática puede producir una gramática libre del contexto determinista y así permitir análisis más eficientes. Generadores de compiladores como YACC incluyen características para resolver algunas clases de ambigüedad, como la utilización de la precedencia y restricciones de asociatividad.
Lenguajes inherentemente ambiguos
La existencia de lenguajes inherentemente ambiguos fue demostrada con el Teorema de Parikh en 1961 por Rohit Parikh en un informe de investigación del MIT.[5]
Mientras algunos lenguajes libres del contexto (el conjunto de cadenas que puede ser generado por una gramática) tienen tanto gramáticas ambiguas como no-ambiguas, existen lenguajes libres del contexto para los que no existe una GLC no-ambigua. Un ejemplo de un lenguaje inherentemente ambiguo es la unión de con . Este conjunto es libre del contexto, dado que la unión de dos lenguajes libres del contexto es siempre libre del contexto. Pero Hopcroft y Ullman (1979) brindaron una demostración de que no hay ninguna manera de analizar cadenas sintácticamente en forma no-ambigua en el subconjunto común .[6]
Véase también
- Chart parser, otro tipo de analizador sintáctico para gramáticas ambiguas
Referencias
- Hopcroft, John; Motwani, Rajeev; Ullman, Jeffrey (2001). Introduction to automata theory, languages, and computation (2nd edición). Addison-Wesley. Theorem 9.20, pp. 405–406. ISBN 0-201-44124-1.
- Axelsson, Roland; Heljanko, Keijo; Lange, Martin (2008). «Analyzing Context-Free Grammars Using an Incremental SAT Solver». Proceedings of the 35th International Colloquium on Automata, Languages and Programming (ICALP'08), Reykjavik, Iceland. Lecture Notes in Computer Science 5126. Springer-Verlag. pp. 410-422. doi:10.1007/978-3-540-70583-3_34. (requiere suscripción).
- Knuth, D. E. (July 1965). «On the translation of languages from left to right». Information and Control 8 (6): 607-639. doi:10.1016/S0019-9958(65)90426-2. Archivado desde el original el 15 de marzo de 2012. Consultado el 29 de mayo de 2011.
- Hopcroft, John; Motwani, Rajeev; Ullman, Jeffrey (2001). Introduction to automata theory, languages, and computation (2nd edición). Addison-Wesley. pp. 249-253. ISBN 0-201-44124-1.
- Language-generating devices. Quarterly Progress Report, Research Laboratory of Electronics, MIT. January 1961.
- p.99-103, Sect.4.7
Enlaces externos
- dk.brics.Gramática - un analizador de ambigüedad de gramáticas
- CFGAnalyzer - Herramienta para analizar gramáticas libres del contexto con respecto a universalidad de lenguaje, ambigüedad, y propiedades similares.