Gran teorema de Poncelet
En geometría, el gran teorema de Poncelet (también conocido como "porisma de Poncelet" o "teorema de cierre de Poncelet") establece que siempre que un polígono está inscrito en una sección cónica y circunscrito en otra, el polígono debe ser parte de una familia infinita de polígonos que están todos inscritos y circunscriben a las mismas dos cónicas.[1][2] Lleva el nombre del ingeniero y matemático francés Jean-Victor Poncelet.
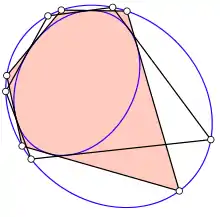
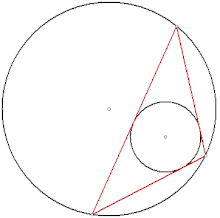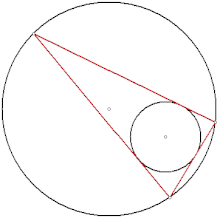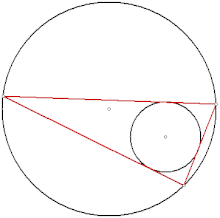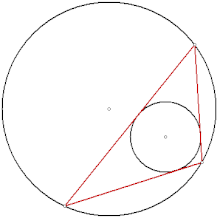
El porismo de Poncelet puede ser probado mediante un argumento que usa una curva elíptica, cuyos puntos representan una combinación de una línea tangente a una cónica y un punto de cruce de esa línea con la otra cónica.
Planteamiento
Sean C y D dos cónicas en un mismo plano. Si es posible encontrar para un n > 2, un polígono de n lados que simultáneamente se inscribe en C (lo que significa que todos sus vértices se encuentran en C) y circunscrito alrededor de D (lo que significa que todos sus bordes son tangentes a D), entonces es posible encontrar un número infinito de ellos. Cada punto de C o D es un vértice o una tangencia (respectivamente) de uno de dichos polígonos.
Si las cónicas son circunferencias, los polígonos que están inscritos en un círculo y circunscritos sobre el otro se llaman polígonos bicéntricos, por lo que este caso especial del porismo de Poncelet se puede expresar de manera más concisa al decir que cada polígono bicéntrico es parte de una familia infinita de polígonos bicéntricos con respecto a los mismos dos círculos.[3]: p. 94
Demostración proyectiva
Considérense C y D como curvas en el plano proyectivo complejo P2. Para simplificar, supóngase que C y D se cruzan (lo que significa que cada punto de intersección entre ambas es un cruce simple). En consecuencia, mediante el teorema de Bézout, la intersección C ∩ D de las dos curvas consta de cuatro puntos complejos. Para un punto arbitrario d en D, se define ℓd, la recta tangente a D en d. Sea X la subvariedad de C × D que consta de (c, d) tal que ℓd pasa a través de c. Dado c, el número de d con (c, d) ∈ X es 1 si c ∈ C ∩ D y 2 de lo contrario. Por lo tanto, la proyección X → C ≃ P1 representa X como un recubrimiento de grado 2 ramificado sobre 4 puntos, por lo que X es una curva elíptica (una vez que se fija un punto base en X). Sea la involución de X haciendo corresponder un punto general (c, d) al otro punto (c, d' ) con la misma primera coordenada. Cualquier involución de una curva elíptica con un punto fijo, cuando se expresa en la ley del grupo, tiene la forma x → p - x para algunos p, por lo que tiene esta forma. De forma similar, la proyección X → D es un morfismo de grado 2 ramificado sobre los puntos de contacto en D de las cuatro rectas tangentes a ambos C y D, y la involución correspondiente tiene la forma x → q - x para algunos q. Por lo tanto, la composición es una traslación en X. Si una potencia de tiene un punto fijo, esa potencia debe ser la identidad. Trasladado de nuevo al lenguaje de C y D, esto significa que si un punto c ∈ C (relacionado con un correspondiente d) da lugar a una órbita que se cierra (es decir, da un ene-ágono), entonces también lo hace cada punto. Los casos degenerados en los que C y D no son transversales se contemplan como un caso límite.
Variaciones y generalizaciones
Teorema de Cayley
Sea la circunferencia , y la elipse . Luego, la condición del bucle en cadena se da en términos de la serie de Taylor de la función . (Cada coeficiente se calcula a través de y , por ejemplo, ). Debe saberse que:
1) La cadena de Poncelet de los pares y se enlaza con los pasos si y solo si
2) El bucle de Poncelet de los pares y se enlaza en los pasos si y solo si[4]
Teorema de Schwarz
Sea una cadena de Poncelet. Denominando a la línea , considérense los puntos de intersección . Luego, para cualquier número entero ,
- Todos los puntos se encuentran en una sección cónica
- Todos los puntos se encuentran en una sección cónica
Véase también
- Elipse de Hartshorne
- Cadena de Steiner
- Rectas tangentes a un círculo
Referencias
- Weisstein, Eric W. "Poncelet's Porism." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PonceletsPorism.html
- King, Jonathan L. (1994). «Three problems in search of a measure». Amer. Math. Monthly 101: 609-628. doi:10.2307/2974690.
- Johnson, Roger A., Advanced Euclidean Geometry, Dover Publications, 2007 (orig. 1960).
- Dragović, Vladimir, Radnović, Milena. (2011). «Poncelet Porisms and Beyond». Frontiers in Mathematics (Springer). p. 116. ISBN 3034800142.
Bibliografía
- Bos, H. J. M.; Kers, C.; Oort, F.; Raven, D. W. "Poncelet's closure theorem". Expositiones Mathematicae 5 (1987), no. 4, 289–364.
Enlaces externos
- David Speyer sobre el Porismo de Poncelet
- RE. Fuchs, S. Tabachnikov, "Omnibus matemático: treinta conferencias sobre matemáticas clásicas"
- applet interactivo de Michael Borcherds que muestra los casos n = 3, 4, 5, 6, 7, 8 (incluidos los casos convexos para n = 7, 8) realizados utilizando GeoGebra.
- Interactive applet de Michael Borcherds mostrando el Porismo de Poncelet para una Elipse general y una Parábola realizadas usando GeoGebra.
- Interactive applet de Michael Borcherds que muestra el Porismo de Poncelet para 2 elipses generales (orden 3) realizadas utilizando GeoGebra.
- Interactive applet de Michael Borcherds mostrando el Porismo de Poncelet para 2 elipses generales (orden 5) realizadas usando GeoGebra.
- Interactive applet de Michael Borcherds mostrando el Porismo de Poncelet para 2 elipses generales (orden 6) realizadas usando GeoGebra.
- Java applet mostrando el caso exterior para n = 3 en la Universidad Nacional de Tsing Hua.
- Artículo sobre el Porísmo de Poncelet en Mathworld.