Hexapawn

Hexapawn (o hexapeón) es un juego determinista para dos jugadores inventado por Martin Gardner.[1] Se juega en un tablero rectangular de tamaño variable, por ejemplo en un tablero de 3 × 3 o en un tablero de ajedrez. En un tablero de tamaño n × m, cada jugador comienza con m peones, uno por cada casilla de la fila más cercana a ellos. El objetivo de cada jugador es hacer avanzar uno de sus peones al extremo opuesto del tablero o evitar que el otro jugador se mueva.[2][3]

Un tablero de hexapeón de 3×3.

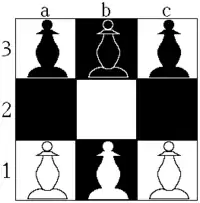
El Hexapawn en el tablero de 3 × 3 es un juego resuelto; con un juego perfecto, las blancas siempre perderán en 3 jugadas: (1.b2 axb2 2.cxb2 c2 3.a2 c1 #). De hecho, Gardner lo construyó específicamente como un juego con un pequeño árbol de juego, con el fin de demostrar cómo podría ser interpretado por una inteligencia artificial heurística implementada por un equipo mecánico basado en el motor del Matchbox Educable Noughts and Crosses (para el tres en línea) de Donald Michie.[4]

Una variante de este juego es octopawn, que se juega en un tablero de 4 × 4 con 4 peones en cada lado. En octopawn, si ambos jugadores juegan bien, el segundo jugador que se mueva siempre perderá.

Historia

Martin Gardner ideó un juego para ilustrar con un ejemplo simple la posibilidad de construir un "robot de fósforos", una máquina de autoaprendizaje, que consta de 24 cajas de fósforos con cuentas de colores. Una máquina de tic-tac-toe similar consta de 300 cajas de cerillas.[5][6] El juego apareció en la sección Mathematical Games de la revista Scientific American en marzo de 1962.[7]

En 1967, el juego fue utilizado por D. Bagley en su disertación,[8] en la que también se introdujo el término “algoritmo genético”.[9]

Generalizaciones

El juego es posible en las juntas de otros tamaños,[10] en particular, 4×4 ("Octapawn") o n×3 (anchura n celdas). El artículo de John R. Brown [11] proporciona un análisis completo de la variación "amplia" del juego; si el ancho del tablero es de n celdas, entonces el jugador que realiza el primer movimiento tiene una estrategia ganadora si y solo si el último dígito del número n es 1, 4, 5, 7 u 8.[12]

Reglas

Como en el ajedrez, cada peón puede moverse de dos formas diferentes: puede moverse una casilla hacia adelante o puede capturar un peón una casilla en diagonal por delante de él. Un peón no puede moverse hacia adelante si hay un peón en la siguiente casilla. A diferencia del ajedrez, el primer movimiento de un peón no puede avanzar dos espacios. Un jugador pierde si no tiene movimientos legales o si el otro jugador llega al final del tablero con un peón.

Ajedrez de Dawson

Siempre que un jugador avanza un peón a la penúltima fila (a menos que sea un peón aislado) existe la amenaza de pasar a la última fila mediante captura. Por lo tanto, las únicas respuestas sensatas del oponente son capturar el peón avanzado o avanzar el amenazado, siendo esto último solo sensible en el caso de que haya un peón amenazado en lugar de dos. Si uno restringe 3 × N hexapawn con la regla adicional de que la captura es siempre obligatoria, el resultado es el ajedrez de Dawson.

El ajedrez de Dawson se reduce al juego imparcial denotado .137 en la notación de Conway. Esto significa que es equivalente a un juego similar a Nim en el que:

  • en un turno, el jugador puede quitar uno a tres objetos de un montón,
  • eliminar solo un objeto es un movimiento legal solo si el objeto eliminado es el único objeto en el montón, y
  • al retirar tres objetos de un montón de cinco o más, el jugador también puede dividir el resto en dos montones.

La posición inicial es una sola pila de tamaño N. La secuencia nim para este juego es

0.1120311033224052233011302110452740
  1120311033224455233011302110453748
  1120311033224455933011302110453748
  1120311033224455933011302110453748
  1120311033224455933011302110453748 ...,

donde las entradas en negrita indican los valores que difieren del eventual comportamiento periódico de la secuencia.

Referencias
  1. Gardner, Martin (marzo de 1962). «Mathematical Games». Scientific American.
  2. «Hexapawn». web.archive.org. 30 de marzo de 2005. Archivado desde el original el 30 de marzo de 2005. Consultado el 31 de enero de 2021.
  3. Gardner, 1972, pp. 170—171.
  4. «Javazoid - Java articles, links, code». web.archive.org. 16 de junio de 2008. Archivado desde el original el 16 de junio de 2008. Consultado el 31 de enero de 2021.
  5. Gardner, 1972, p. 170.
  6. Gardner, 1991, p. 93.
  7. Martin Gardner (1962-03). «How to build a game-learning machine and then teach it to play and to win». Mathematical Games. Scientific American. Archivado desde el original el 19 de abril de 2016.
  8. John D. Bagley (1967). The behavior of adaptive systems which employ genetic and correlation algorithms.
  9. James Kennedy, Russell C. Eberhart, Yuhui Shi (2001). Swarm Intelligence. Academic Press. p. 137. ISBN 1-55860-595-9.
  10. Averbach, Bonnie; Orin, Chein (1999). Problem Solving Through Recreational Mathematics. Dover Books on Mathematics. ISBN2: 9780486409177. Courier Corporation. p. 264. ISBN 0486409171.
  11. John R. Brown (11 de 1965). «Extendapawn — An Inductive Analysis». Mathematics Magazine (magazine) (en inglés) (38): 286—299.
  12. Gardner, 1972, p. 179.

Bibliografía
  • Gardner, Martin (1972). Ocio matemático (en ruso). Editorial Mir.
  • Gardner, Martin (1992). The Unexpected Hanging and Other Mathematical Diversions (en inglés). University Of Chicago Press. ISBN 9780226282565.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.