Hipótesis del arrastre del éter
En el siglo XIX, la teoría del éter lumínico como el medio hipotético para la propagación de la luz era ampliamente discutida. Una parte importante de esta discusión era la cuestión respecto del estado de movimiento de la Tierra con respecto a este medio. La hipótesis del arrastre del éter trató la cuestión de si el éter lumínico era arrastrado o permeaba los objetos en movimiento. Según la primera idea, ningún movimiento relativo existía entre la Tierra y el éter; según la segunda, el movimiento relativo existe y por ello la velocidad de la luz tendría que depender de la velocidad de este movimiento ("viento del éter") que tendría que ser medible por instrumentos estacionarios sobre la superficie de la Tierra. Modelos específicos del éter fueron ideados por Augustin-Jean Fresnel, quien en 1818 propuso que el éter es parcialmente arrastrado por la materia. El otro modelo fue propuesto por George Stokes en 1845, donde el éter se desplazaba por completo en el interior o en las proximidades de la materia en movimiento.
Mientras que la teoría casi-estacionaria de Fresnel era aparentemente confirmada por el experimento de Fizeau (1851), la teoría de Stokes era aparentemente confirmada por el experimento de Michelson–Morley (1881, 1887). Esta situación contradictoria fue resuelta por los trabajos de Hendrik Antoon Lorentz (1895, 1904), cuya teoría del éter de Lorentz eliminó cualquier forma de arrastre del éter, y finalmente con el trabajo de Albert Einstein (1905), cuya teoría de la relatividad especial no contempla el éter como medio mecánico en absoluto.[1][2][3]
Arrastre parcial del éter
En 1810, François Arago se dio cuenta de que las variaciones en el índice de refracción de una sustancia pronosticadas por la teoría corpuscular, proporcionarían un método útil para medir la velocidad de la luz. Estas predicciones surgieron porque el índice de refracción de una sustancia como el vidrio depende de la proporción de las velocidades de la luz en el aire y en el vidrio. Arago intentó medir la extensión a la que los corpúsculos de luz serían refractados por un prisma de vidrio situado delante de un telescopio. Esperaba que hubiese una gama de ángulos de refracción diferentes debido a la variedad de velocidades distintas de las estrellas y al movimiento de la tierra en momentos diferentes del día y del año. Contrariamente a esta expectativa, encontró que no había ninguna diferencia en la refracción entre las estrellas, independientemente del momento del día o las estaciones. Todo lo que Arago observó fue la aberración estelar normal.[4]
En 1818, Augustin-Jean Fresnel examinó los resultados de Arago usando una teoría ondulatoria de la luz. Se dio cuenta de que incluso si la luz era transmitida como una onda, el índice de refracción del contacto entre el vidrio y el aire tendría que haber variado cuando el vidrio se desplazase a través del éter para interceptar las ondas de luz con velocidades diferentes cuando la tierra en rotación y las estaciones cambiaban. Fresnel propuso que el prisma de vidrio arrastraría algo del éter junto con él, de modo que "..el éter queda en exceso dentro del prisma".[5] Se dio cuenta de que la velocidad de propagación de las ondas depende de la densidad del medio, por lo que propuso que la velocidad de la luz en el prisma necesitaría ser ajustada por una cantidad de arrastre. La velocidad de la luz en el vidrio sin ningún ajuste vendría dada por:
El ajuste del arrastre viene dado por:
donde es la densidad del éter en el entorno, es la densidad del éter en el vidrio, y es la velocidad del prisma con respecto al éter.
El factor puede ser escrito como porque el índice de refracción, n, sería dependiente de la densidad del éter. Este cociente es conocido como el coeficiente de arrastre de Fresnel. La velocidad de la luz en el vidrio entonces viene dada por:
Esta corrección era capaz de explicar el resultado nulo del experimento de Arago. Introducía el concepto de un éter en gran parte estacionario, arrastrado por sustancias como el vidrio, pero no por el aire. Su éxito favoreció la teoría ondulatoria de la luz sobre la teoría corpuscular anterior.
Problemas del arrastre parcial del éter
El coeficiente de arrastre de Fresnel pareció directamente confirmado por el experimento de Fizeau y sus repeticiones. En general, con la ayuda de este coeficiente, el resultado negativo de todos los experimentos ópticos sobre el éter, bastante sensibles en principio para detectar efectos de primer orden (como los experimentos de Arago, Fizeau, Hoek, Airy y Mascart) pudieron ser explicados. La idea de un éter (casi) estacionario es también compatible con el fenómeno de la aberración estelar. Aun así, esta teoría se consideró refutable por las razones siguientes:[1][2][3]
- Ya se sabía en el siglo XIX que el arrastre parcial del éter requiere velocidades relativas distintas para la luz de colores diferentes (lo que evidentemente no es el caso del modelo de Fresnel).
- La teoría de Fresnel con un éter (casi) estacionario pronostica resultados positivos para experimentos con capacidad para detectar efectos de segundo orden. Aun así, ensayos como el experimento de Michelson–Morley y el experimento de Trouton–Noble, dieron resultados negativos y eran por tanto refutaciones directas del éter de Fresnel.
Arrastre completo del éter
Para George Stokes (1845) el modelo de un éter totalmente independiente o sólo parcialmente afectado por la materia en movimiento era antinatural y poco convincente, así que supuso que el éter es completamente arrastrado en el interior y en la proximidad de la materia, parcialmente arrastrado en distancias más grandes, y estacionario en el resto del espacio libre.[6][7][8][9] También Heinrich Rudolf Hertz (1890) incorporó un modelo de éter totalmente arrastrado dentro de su reelaboración de la teoría de Maxwell del electromagnetismo, para situarlo de acuerdo con el principio galileano de relatividad. Si se supone que el éter está dentro de la materia en un marco de referencia en reposo, la transformación galileana da como resultado que la materia y el éter (incluido en su interior) viajen con la misma velocidad en otro marco de referencia.[1]
Problemas del arrastre completo del éter

El arrastre completo del éter puede explicar el resultado negativo de todos los experimentos de deriva del éter (como el de Michelson–Morley). Aun así, esta teoría se consideraba incorrecta por las razones siguientes:[1][10]
- El experimento de Fizeau (1851) indicaba sólo un arrastre parcial de la luz.
- El efecto Sagnac muestra que dos rayos de luz, emanados de la misma fuente en direcciones diferentes en una plataforma en rotación, requieren tiempos diferentes para volver a su origen. Aun así, si el éter es completamente arrastrado por la plataforma, este efecto no tendría que ocurrir en absoluto.
- Oliver Lodge realizó experimentos en la década de 1890, buscando evidencias de que la propagación de la luz está influida por la proximidad de grandes masas en rotación, y no encontró tal influencia.[11][12]
- En el experimento de Hammar, realizado por Gustaf Wilhelm Hammar en 1935, se utilizó un interferómetro de trayectoria común. Bloques de plomo masivos fueron instalados a ambos lados de un interferómetro de un solo brazo. Este montaje tendría que causar cantidades diferentes de arrastre del éter y por lo tanto producir un resultado positivo. Aun así, el resultado fue otra vez negativo.[13]
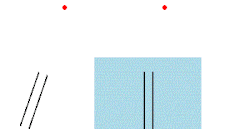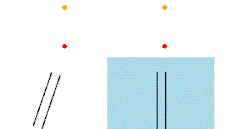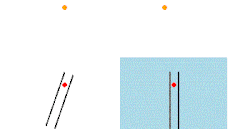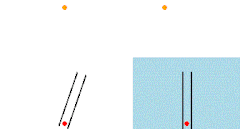
- Es inconsistente con el fenómeno de la aberración estelar. Así, la posición de una estrella cuando es observada con un telescopio fluctúa a cada lado de una posición central aproximadamente 20,5 segundos de arco cada seis meses. Este balanceo es la cantidad esperable cuando se considera la velocidad con la que la tierra recorre su órbita. En 1871 Airy demostró que la aberración estelar se produce incluso cuando el tubo de un telescopio se llena con agua. Parecía que si la hipótesis del arrastre del éter era cierta, entonces la aberración estelar no ocurriría porque la luz viajaría con el éter, que se movería junto con el telescopio. Si se considera un cubo de agua en un tren a punto de entrar en un túnel, y una gota de agua que cae de la entrada del túnel hacia el centro del cubo, la gota no caerá en el centro del fondo del cubo. El cubo es análogo al tubo de un telescopio, la gota es un fotón y el tren es la tierra. Si el éter es arrastrado, entonces la gota viajaría con el tren mientras cae, alcanzando el centro del fondo del cubo. El valor de la aberración estelar, , viene dado por:
- Y por lo tanto: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \tan(\alpha) = \frac{v}{c}}
- La velocidad con la que la Tierra viaja alrededor del sol, v = 30 km/s, y la velocidad de la luz es c = 299.792,458 km/s, lo que da = 20.5 segundos de arco cada seis meses. Esta cantidad de aberración está comprobada y repetidamente observada, contradiciendo la hipótesis del arrastre completo del éter .
Respuestas de Stokes a estos problemas
Ya en 1845, Stokes introdujo algunas suposiciones adicionales para acomodar su teoría de acuerdo con los resultados experimentales. Para explicar el fenómeno de la aberración, supuso que el éter era incompresible e irrotacional, lo que daría, en conexión con su modelo concreto de arrastre del éter, la ley correcta de la aberración.[6] Para reproducir el coeficiente de arrastre de Fresnel (y por tanto, para explicar el experimento de Fizeau) argumentó que el éter es completamente arrastrado dentro de un medio – por ejemplo, se condensa cuando se introduce en un medio y se rarifica cuando sale de él, lo que modifica la velocidad del éter al igual que la de la luz, con las mismas ventajas que las expresiones de Fresnel.[7]
Aunque la teoría de la aberración de Stokes fue considerada viable durante algún tiempo, tuvo que abandonarse porque Lorentz argumentó en 1886 que si el éter es incompresible y tiene la misma componente normal de velocidad que la Tierra, no podría tener la misma componente tangencial de velocidad, por lo que todas las condiciones impuestas por Stokes no se podían cumplir al mismo tiempo.[14]
Arrastre gravitatorio del éter
Otra versión del modelo de Stokes fue propuesto por Theodor des Coudres y Wilhelm Wien (1900). Supusieron que el arrastre del éter es proporcional a la masa gravitacional. Esto es, el éter es completamente arrastrado por la tierra, y sólo parcialmente arrastrado por objetos más pequeños en su superficie.[15] Para salvar la explicación de la aberración dada por Stokes, Max Planck (1899) argumentó en una carta dirigida a Lorentz, que el éter no podría ser incompresible, pero que si era condensado por la gravitación en la proximidad de la Tierra, esto daría las condiciones necesarias para verificar la teoría de Stokes ("teoría de Stokes-Planck"). Cuando se comparaba con los experimentos anteriores, este modelo podía explicar los resultados positivos de los experimentos de Fizeau y Sagnac, porque la masa pequeña de aquellos instrumentos podía arrastrar el éter solo parcialmente (o en absoluto), y por la misma razón explicaba el resultado negativo de los experimentos de Lodge. Es también compatible con los experimentos de Hammar y de Michelson–Morley, cuando el éter es completamente arrastrado por la gran masa de la Tierra.
Aun así, esta teoría era directamente refutada por el experimento de Michelson-Gale-Pearson (1925). La principal objeción de este experimento contra el anterior experimento de Sagnac es el hecho de que se consideraba la rotación propia de la Tierra sobre su eje. Si el éter era completamente arrastrado por el campo gravitatorio de la Tierra, se debería esperar un resultado negativo, pero el resultado obtenido fue positivo.[10]
Y desde un punto de vista teórico, Hendrik Antoon Lorentz hizo notar que la hipótesis de Stokes-Planck requiere que la velocidad de la luz no fuese afectada por un aumento de densidad de 50.000 veces la del éter, por lo que Lorentz y el mismo Planck rechazaron esta hipótesis por improbable.[1][16]
Lorentz y Einstein
Desde que Lorentz se vio forzado a abandonar la hipótesis de Stokes, escogió el modelo de Fresnel como punto de partida. Fue capaz de reproducir el coeficiente de arrastre de Fresnel en 1892, aunque en la teoría de Lorentz se representaba una modificación de la propagación de las ondas de luz, no el resultado de cualquier arrastre del éter. Por lo tanto, el éter de Lorentz es plenamente estacionario o inmóvil. Aun así, esto llevaba a los mismos problemas que ya habían afligido al modelo de Fresnel: estaba en contradicción con el experimento de Michelson–Morley. Por lo tanto George Francis Fitzgerald (1889) y Lorentz (1892) introdujeron la contracción de longitud, esto es, todo cuerpo se contrae en la línea de su movimiento con el factor . Además, en la teoría de Lorentz la transformación galileana era reemplazada por la transformación de Lorentz.[17]
Aun así, la acumulación de hipótesis para rescatar el concepto del éter estacionario se consideraba muy artificiosa. Fue finalmente Albert Einstein (1905), quien reconoció que basta con asumir el principio de la relatividad y la constancia de la velocidad de la luz en todos los marcos inerciales de referencia, para desarrollar la teoría de la relatividad especial y para deducir por completo la transformación de Lorentz, sin necesidad de utilizar el concepto del éter estacionario.[18]
Como demostró Max von Laue en 1907, la relatividad especial pronostica el resultado del experimento de Fizeau relativo al teorema de adición de la velocidad sin la más mínima necesidad del supuesto del éter. Si es la velocidad de la luz relativa al aparato de Fizeau, es la velocidad de la luz en el agua, y es la velocidad del flujo del agua, entonces:
teniéndose que si v/c es pequeño, puede ser expandido utilizando una expresión binomial para resultar:
Este resultado es idéntico al de la ecuación de Fresnel.[19]
Resumen
En física moderna (basada en la teoría de la relatividad y en la mecánica cuántica), el concepto del éter como una "sustancia material" con un "estado de movimiento" ha desaparecido por completo. Así, cuestiones respecto a un posible "arrastre del éter" no han vuelto a ser consideradas significativas nunca más por la comunidad científica. Lo que de hecho existe, es el arrastre de sistemas de referencias pronosticado por la relatividad general, esto es, las masas en rotación distorsionan el espacio-tiempo métrico, causando una precesión de la órbita de partículas cercanas. Pero este efecto es muchos órdenes de magnitud más débil que cualquier efecto de "arrastre del éter" comentado en este artículo.
Véase también
- Historia de relatividad especial
- Pruebas de la relatividad especial
- Pruebas de la relatividad general
- Arrastre de referencias
Bibliografía y referencias
- Whittaker, Edmund Taylor (1910), A History of the theories of aether and electricity (1. edición), Dublin: Longman, Green and Co..
- Jannsen, Michel & Stachel, John (2008), The Optics and Electrodynamics of Moving Bodies.
- Rafael Ferraro and Daniel M Sforza (2005), «Arago (1810): the first experimental result against the ether», Eur. J. Phys. 26: 195-204, Bibcode:2005EJPh...26..195F, arXiv:physics/0412055, doi:10.1088/0143-0807/26/1/020.
- Arago, A. (1810–1853), «Mémoire sur la vitesse de la lumière, lu à la prémière classe de l’Institut, le 10 décembre 1810», Comptes Rendus de l'Académie des Sciences 36: 38-49.
- Fresnel, A. (1818), «Lettre d'Augustin Fresnel à François Arago sur l'influence du mouvement terrestre dans quelques phénomènes d'optique», Annales de chimie et de physique 9: 57-66.
- Stokes, George Gabriel (1845), «On the Aberration of Light», Philosophical Magazine 27: 9-15, doi:10.1080/14786444508645215.
- Stokes, George Gabriel (1846), «On Fresnel's Theory of the Aberration of Light», Philosophical Magazine 28: 76-81, doi:10.1080/14786444608645365.
- Stokes, George Gabriel (1846), «On the Constitution of the Luminiferous Æther, viewed with reference to the phænomenon of the Aberration of Light», Philosophical Magazine 29: 6-10, doi:10.1080/14786444608562589.
- Stokes, George Gabriel (1848), «On the Constitution of the Luminiferous Æther», Philosophical Magazine 32: 343-349, doi:10.1080/14786444808645996.
- Georg Joos: Lehrbuch der theoretischen Physik. 12. edition, 1959, page 448
- Lodge, Oliver J. (1893), «Aberration Problems», Philosophical Transactions of the Royal Society A 184: 727-804, Bibcode:1893RSPTA.184..727L, doi:10.1098/rsta.1893.0015.
- Lodge, Oliver J. (1897), «Experiments on the Absence of Mechanical Connexion between Ether and Matter», Philosophical Transactions of the Royal Society A 189: 149-166, Bibcode:1897RSPTA.189..149L, doi:10.1098/rsta.1897.0006.
- G. W. Hammar (1935), «The Velocity of Light Within a Massive Enclosure», Physical Review 48 (5): 462-463, Bibcode:1935PhRv...48..462H, doi:10.1103/PhysRev.48.462.2.
- Lorentz, Hendrik Antoon (1886), «De l'influence du mouvement de la terre sur les phénomènes lumineux», Archives néerlandaises des sciences exactes et naturelles 21: 103-176.
- Wien, Wilhelm (1898), «Über die Fragen, welche die translatorische Bewegung des Lichtäthers betreffen (Referat für die 70. Versammlung deutsche Naturforscher und Aerzte in Düsseldorf, 1898)», Annalen der Physik (Beilage) 301 (3): I-XVIII.
- Lorentz, H.A. (1899), «Stoke's Theory of Aberration in the Supposition of a Variable Density of the Aether», Proceedings of the Royal Society 1: 443-448, Bibcode:1898KNAB....1..443L, archivado desde el original el 4 de abril de 2008.
- Lorentz, Hendrik Antoon (1904), «Electromagnetic phenomena in a system moving with any velocity smaller than that of light», Proceedings of the Royal Netherlands Academy of Arts and Sciences 6: 809-831.
- Einstein, Albert (1905), «On the Electrodynamics of Moving Bodies», Annalen der Physik 322 (10): 891-921, Bibcode:1905AnP...322..891E, doi:10.1002/andp.19053221004..
- Laue, Max von (1907), «Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip» [The Entrainment of Light by Moving Bodies in Accordance with the Principle of Relativity], Annalen der Physik (en alemán) 23 (10): 989-990, Bibcode:1907AnP...328..989L, doi:10.1002/andp.19073281015.
- Wikibooks: Special Relativity
- Resnick, Robert, Basic Concepts in Relativity and Early Quantum Theory, 1972, John Wiley and Sons Inc.
Enlaces externos
- Mathpages: Stokes’ Mistake