Homotecia

Sea B un espacio vectorial sobre un cuerpo ${\displaystyle \scriptstyle \mathbb {K} }$. Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada ${\displaystyle \scriptstyle h_{C,k}}$ envía un punto M del espacio sobre el punto M' tal que:

(1a)${\displaystyle M'-C=k(M-C)\,}$

La anterior puede también ser una transformación afín de la forma:

(1b)${\displaystyle M'=kM+(1-k)C\,}$

La anterior relación puede escribirse vectorialmente en el plano como:

${\displaystyle {\begin{bmatrix}m'_{x}\\m'_{y}\\1\end{bmatrix}}={\begin{bmatrix}k&0&(1-k)c_{x}\\0&k&(1-k)c_{y}\\0&0&1\end{bmatrix}}{\begin{bmatrix}m_{x}\\m_{y}\\1\end{bmatrix}}}$

Donde: ${\displaystyle M'=(m'_{x},m'_{y})\,}$, ${\displaystyle M=(m_{x},m_{y})\,}$ y ${\displaystyle C=(c_{x},c_{y})\,}$.
En tres o más dimensiones la fórmula anterior se generaliza trivialmente.

La homotecia es una composición de una transformación lineal y una traslación, y por consiguiente conserva:

1. el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura
2. el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C']
3. La imagen de línea es otra línea paralela a la original.
4. el paralelismo: dos líneas paralelas tienen imágenes paralelas. En la figura (B'E') // (C'D') porque (BE) //(CD).
   
5. Si k ≠ 1, el centro de la homotecia es el único punto fijo (k = 1 corresponde a la identidad de E: todos los puntos son fijos).
6. k = - 1 corresponde a una simetría de centro C.
7. Si k ≠ 0, ${\displaystyle \scriptstyle h_{C,k}}$ admite como trasformación recíproca ${\displaystyle \scriptstyle h_{C,1/k}}$ (cuando k = 0, no es biyectiva).
8. Al componer dos homotecias del mismo centro se obtiene otra homotecia con este centro, cuya razón es el producto de las razones de las homotecias iniciales: ${\displaystyle \scriptstyle h_{C,k}}$ o ${\displaystyle \scriptstyle h_{C,k'}}$ = ${\displaystyle \scriptstyle h_{C,k\cdot k'}}$.
9. Al componer homotecias de centros distintos, de razones k y k', se obtiene una homotecia de razón k·k' cuando k·k'≠1, y una traslación si k·k'=1. El conjunto de las homotecias (con k≠0) y las translaciones forman un grupo.

Cuando K es mayor que cero es k mayor Cuando el cuerpo de escalares son los Reales, se cumple que:

1. todas las longitudes son multiplicadas por |k|, el valor absoluto de la razón.
2. el cociente de longitudes es conservado: A'C'/B'E' = AC/BE en la figura
3. los ángulos orientados son conservados, en particular los ángulos rectos. Es obvio en la figura.

Más aún:

1. k = - 1 corresponde a la simetría de centro C que es la rotación alrededor de C de ángulo π radianes (180°).
   
2. |k| > 1 implica una ampliación de la figura.
   
3. |k| < 1 implica una reducción.
   
4. k < 0, la homotecia se puede expresar como la composición de una simetría con una homotecia de razón |k|, ambas de igual centro. Que la homotecia original.

Homotecia

En esta sección, los escalares serán números reales.

Una homotecia generalizada en el plano es una transformación del plano en sí mismo en donde una recta y su homóloga son paralelas. De esta definición, se sigue fácilmente que las homotecias conservan ángulos, es decir son transformaciones conformes del plano, que el conjunto de homotecias forman un 'grupo' y que las traslaciones son casos particulares de las homotecias.

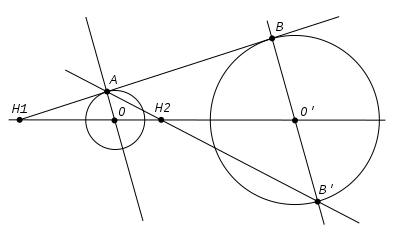
Consideremos la homotecia en la cual la recta OA se transforma en la recta O'B, siendo O' el homólogo de O y B el homólogo de A. Necesariamente, las rectas OO' y AB son invariantes en esta homotecia y el punto H1, centro de la homotecia, es invariante. En esta homotecia la circunferencia de centro O y radio OA se transforma en la circunferencia de centro O' y de radio O'B y la razón de la homotecia es la razón (positiva) de los segmentos O'B y OA.

Si por el contrario, el punto A se transforma en B' entonces la recta AB' es invariante y es el punto H2 el centro de homotecia. En este caso, la razón de la homotecia es negativa.

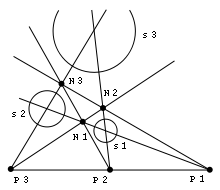
Dadas dos circunferencias, estas siempre se pueden considerar como homotéticas una de la otra.

En la figura de a lado, las líneas de s1, es en la homotecia de razón positiva, con centro en P1, o de razón negativa, con centro de homotecia en N1.

Consideremos las homotecias, una con centro en P1 en la cual la circunferencia S2 es homotética de la circunferencia s1, y la homotecia de centro P3 en la que la circunferencia s3 es homotética a la circunferencia s2. La composición de estas dos homotecias es la homotecia de centro en P2 que transforma la circunferencia s1 en la circunferencia s3. Es por esta razón que los centros de homotecia positivos, P1, P2 y P3 están alineados. En general, dadas tres circunferencias existen seis centros de homotecia, alineados tres a tres sobre cuatro rectas.

Estas rectas son las llamadas ejes de homotecia de las tres circunferencias dadas.

• Punto de fuga.