Interacción lógica
La noción matemática de «interacción lógica», concebida como generalización de la de interacción nacido del Diseño de Experimentos, ha sido introducida a finales de los años 1990. Primero utilizada en análisis de los datos, encontró un campo de aplicación en los modelos de regresión múltiple no postulados.
Noción de interacción
La noción de interacción no debe ser confundida con la de correlación. Hablamos de efecto de interacción cuando una variable que hay que explicar Y es acondicionada por el acoplamiento de dos variables explicativas A y B.
En el ejemplo siguiente, Y no es correlada a A ni a B; pero Y es correlada negativamente al producto A.B. En efecto, Y presenta valores fuertes cuando A.B presenta valores escasos:
A B A.B Y Prueba 1 -1 -1 1 10 Prueba 2 -1 1 -1 21 Prueba 3 1 -1 -1 19 Prueba 4 1 1 1 9
La interacción A.B es también llamada producto cruzado de A y de B.
Un caso particular de tabla de dato
La tabla más arriba es a veces llamado diseño completo de experimentos de 2 niveles. En efecto, cada variable tiene sólo 2 niveles (escaso y fuerte), y todos los casos son considerados, a saber:
- A escaso y B escaso,
- A escaso y B fuerte,
- A fuerte y B escaso,
- A fuerte y B fuerte.
Es un caso particular del diseño completo de experimentos de k niveles.
En un « diseño completo », las variables A, B y A.B son ortogonales, es decir que sus correlaciones son nulas.
El diseño completo mismo es un caso particular del « diseño de experimentos », en el cual las variables explicativas A y B son controladas con un modo razonado para obtener el máximo de información en el mínimo de pruebas.
Por fin, el diseño de experimentos es un caso particular de las tablas de datos , en los cuales las variables explicativas no son forzosamente controladas.
Generalización a las tablas de datos cualesquiera
La noción de interacción lógica, que va a ser introducida a continuación, se aplica las tablas de datos en general, sobre variables cuantitativas y\o cualitativas (con tal que estas últimas utilicen uno codificación disyuntiva completa).
Hay que reducirse a una unidad común de valuación. El uso es de centrar reducir las variables A y B, antes de calcular el producto cruzado AB (variables centradas reducidas tienen una media nula y una desviación típica igual a uno). En estas nuevas unidades, nuestro tabla se hace:
A B A.B Y Prueba 1 -0.866 -0.866 .866 10 Prueba 2 -0.866 0.866 -0.866 21 Prueba 3 0.866 -0.866 -0.866 19 Prueba 4 0.866 0.866 0.866 9
Interpretación física del producto cruzado
La interpretación física del producto de dos variables con lo mismo unidad, como la longitud y la anchura, es fácil (es una superficie).
¿Pero qué significa el efecto sobre Y del producto cruzado A.B de dos variables de unidades diferentes?

- Tres modos de representar la interacción A.B
- Figura 1: A abscisa, B ordenada; y los valores correspondientes de Y. La variable que hay que explicar Y es escaso si A y B son escasos, o bien si A y B son fuertes.
- Figura 2:
- • en rojo: variación de Y con arreglo a A, para B escaso;
- • en azul: variación de Y con arreglo a A, para B fuerte.
- Pues Y varía de modo diferente con arreglo a A, según que B es escaso o fuerte.
- Figura 3: perfiles de variación, con arreglo a la continuación de las pruebas : Y se parece sobre todo a " A*B ". O si se prefiere, Y se es correlada positivamente con A*B y negativamente con A.B.
Estas figuras muestran que Y es fuerte si "A es escaso y B es fuerte", o bien si "A es fuerte y B es escaso".
En otros términos la operación «A*B» = -A.B corresponde al «o exclusivo» de la lógica.
La figura 1 representaba «o exclusivo» en caso de que las variables A y B son discontinuas a dos niveles.
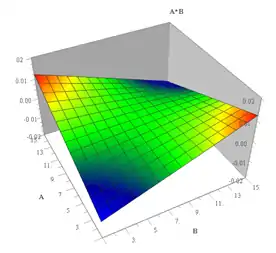
En caso de que las variables A y B son continuas, obtenemos la figura 4 caracterizada por montañas en rojo cuando A es fuerte y B escaso , o bien A es escaso y B es fuerte . En caso contrario, hay unos valles (en azul).
- Figure 4 : superficies de respuesta de la variable A*B.
Noción de interacción lógica
Ya que la variable artificial « A*B ». ' = -A.B corresponde a o exclusiva de la lógica, es natural interesarse también por una interacción lógica mucho más frecuente en física, saber el «y» lógica: «A&B». En el caso de las variables de 2 niveles, la columna A&B tendrá los valores siguientes:
A B A.B A*B A&B Y Prueba 1 -1 -1 1 -1 -1 10 Prueba 2 -1 1 -1 1 -1 21 Prueba 3 1 -1 -1 1 -1 19 Prueba 4 1 1 1 -1 1 9
En el caso general de las variables continuas, tenemos la figura siguiente:
Las figuras siguientes muestran otras interacciones, y se encontrará su descripción a continuación, y las fórmulas matemáticas en referencias.

Significado de los símbolos de interacciones lógicas
f(A,B) Significación La repuesta Y es fuerte cuando... A*B A o-exclusivo B ...A es fuerte y B es escaso o A es escaso y B es fuerte A^B A o B ...A es fuerte o B es fuerte A^-B A o no B ...A es fuerte o B es escaso A&B A y B ...A y B son fuertes A&-B A y no B ...A es fuerte y B es escaso A]B A si B ...A es fuerte si B es fuerte A]-B A si no B ...A es fuerte si B es escaso A}B A si B medio ...A es fuerte si B est medio A{B A moyen si B ...A es medio si B es fuerte A{-B A medio si no B ...A es medio si B es escaso A'B ni A ni B (sentido largo) ...ni A ni B son extrema (son medios) A!B ni A ni B (sentid estricto) ...ni A ni B son extrema (son estrictamente medios) A#B A como B ...A varía como B A+B "A más B" ...suma de A y B (centrados-réducido) es fuerte A-B "A menos B" ...la diferencia de A y B (centrados-réducido) es fuerte
Référencias
Lesty M. (1999) Une nouvelle approche dans le choix des régresseurs de la régression multiple en présence d’interactions et de colinéarités. La revue de Modulad, n°22, janvier 1999, pp. 41-77