Involución (matemática)
En matemática, una involución o función involutiva es una función matemática que es su propia inversa:
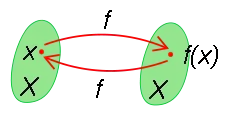
Definida la función:
Esta función cumple la propiedad involutiva si:
para todo x de A, se cumple que la función de la función de x es x.
O, de otra manera:
- ;
Propiedades
Toda involución es una aplicación biyectiva. La función identidad es un ejemplo trivial de involución:
esto es:
para todo a de A, se cumple que la identidad de la identidad de a es a.
El número de involuciones existentes en un conjunto de n elementos viene dado por la siguiente relación de recurrencia:
Los primeros términos de esta secuencia son 1, 1, 2, 4, 10, 26, 76, 232, etc.[1]
Ejemplos
Ejemplos sencillos son la multiplicación por −1 un número real:
dado que:
Para todo x número real, se cumple que el opuesto del opuesto de x es x.
El inverso multiplicativo de números reales sin el cero:
si vemos que:
El complemento de un conjunto en teoría de conjuntos:
dado que:
Los complejos conjugados () en variable compleja; la inversión geométrica; y cifrados como el ROT13 y el de Trithemius.
Véase también
Fuentes y referencias
- Todd A. Ell; Stephen J. Sangwine (2007), «Quaternion involutions and anti-involutions», Computers & Mathematics with Applications 53 (1): 137-143, doi:10.1016/j.camwa.2006.10.029 ..