Lógica de la Refutación y Verificación

La propuesta de Karl Popper para diferenciar las Hipótesis 'científicas' de las 'no científicas' (= 'metafísica') se conoce como criterio de demarcación entre ambas. Este criterio consiste en analizar lógicamente la Hipótesis o la teoría en cuestión, para determinar si es potencialmente 'refutable'. Si lo es, entonces sería una Hipótesis 'científica', de lo contrario sería 'metafísica'. Según este criterio, la religión, el psicoanálisis, el marxismo contemporáneo, la astrología, ..., son todas teorías que tienen sentido, pero están ubicadas en el área 'metafísica', 'no científica'.

El criterio de demarcación popperiano entre ambas áreas del conocimiento, por supuesto no es aceptado por otras corrientes filosóficas, tales como el verificacionismo en sus múltiples variantes ( positivismo, inductivismo, etc.). Estas corrientes consideran como 'científicos' aquellas Hipótesis 'que pueden verificarse empíricamente' , es decir, que puedan comprobarse por medios experimentales, por ejemplo mediante la observación.

Por tanto, los conceptos de REFUTACION y VERIFICACION son claves a la hora de evaluar las dos tendencias principales en la filosofía de la ciencia. Hay que mostrar las diferencias lógicas estructurales de ambas concepciones para poder extraer las conclusiones pertinentes. A continuación la estructura lógica de ambas posiciones sobre la base de las tablas de verdad correspondientes:

H = Hipótesis, premisa, teoría, conjetura, ...

C = Conclusión, predicción, enunciado básico, instancia refutadora, ...

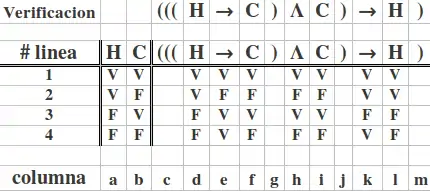
La refutación es una tautología. Queda demostrado por la columna l), debido a que en ella todos los valores son verdaderos.

Las conclusiones Falsas no pueden destruir una afirmación refutadora. En las líneas 2 y 4 las conclusiones son Falsas y sin embargo, la afirmación como un todo sigue siendo Verdadera. Por eso el Modus tollendo tollens representado aquí, es irrefutable, tanto lógica como empíricamente, tal como sucede también con los teoremas matemáticos.

H = Hipótesis, premisa, teoría, conjetura, ...

C = Conclusión, predicción, enunciado básico, instancia verificadora, ...

La verificación no es una tautología. La columna k) es verdadera solo en 'algunos' de los casos posibles (3 de un total de 4). Es falsa en la línea #3.

De la verdad de las conclusiones no se puede inferir la verdad de la Hipótesis. En la línea #1 y #3, la conclusión es verdadera. Sin embargo la Hipótesis respectiva puede ser tanto verdadera (línea #1) como falsa (línea #3). Por tanto la Hipótesis sigue siendo hipotética, teórica, no verdadera.

En este ejemplo se viola el principio anterior : "Hay 100 observaciones comprobadas científicamente, verdaderas, deducidas correctamente de mi Hipótesis XY, por tanto, mi Hipótesis XY también es verdadera ! ". Precisamente aquí esta el error lógico, denominado inducción. Debería decirse en cambio, la Hipótesis sigue siendo hipotética, teórica, una conjetura, sin validez positiva demostrable como tal.

La llamada 'asimetría entre refutación y verificación' consiste, desde un punto de vista lógico, entre la asimetría entre una tautología y una 'no tautología'.