Aplicación de Poincaré

En matemáticas, y en particular en el campo de sistemas dinámicos, un mapa de Poincaré o primer mapa de recurrencia, es una aplicación definida no en el espacio de estados del sistema, sino en un subespacio de dimensión inferior llamado sección de Poincaré. Dicha aplicación lleva cada punto de dicha sección en el primer punto en el que la órbita que lo contiene retorna a la misma. Fue presentada por Henri Poincaré en 1881, quien la aplicó al estudio del problema de los tres cuerpos.

En la sección de Poincaré S, la aplicación de Poincaré P lleva el punto x de en el punto P(x).

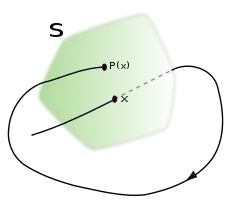
Se exige que la sección de Poincaré sea transversal al flujo del sistema. Dicha transversalidad plasma la exigencia de que las órbitas que comienzan en la sección fluyan a través de la misma y no paralelas a ella.

Una aplicación de Poincaré puede interpretarse como un sistema dinámico discreto con un espacio de estado con menor dimensión que el sistema continuo original. Como preserva algunas características esenciales del sistema original suele emplearse como un medio alternativo de analizar al mismo. Sin embargo, no siempre es posible hacer esto, puesto que no existe un método general para construir aplicaciones de Poincaré. La elección de la misma suele ir precedida de un análisis de la estabilidad lineal del sistema, para asegurar que la sección interseque a todas las órbitas de interés. La correspondencia entre una y otra visión es la siguiente:

• Una órbita periódica simple del sistema dinámico original se convierte en un único punto fijo en la sección de Poincaré.
• Una trayectoria cuasiperiódica en la imagen de una curva cerrada.
• Un movimiento caótico en una zona con puntos distribuidos de modo errático.