María Gaetana Agnesi
María Gaetana Agnesi (Milán, 16 de mayo de 1718-Milán, 9 de enero de 1799) fue una filósofa, matemática, lingüista, filántropa, escritora y teóloga italiana
| María Gaetana Agnesi | ||
|---|---|---|
 | ||
| Información personal | ||
| Nombre en italiano | Maria Gaetana Agnesi | |
| Nacimiento |
16 de mayo de 1718 Milán (Ducado de Milán) | |
| Fallecimiento |
9 de enero de 1799 (80 años) Milán (República Cisalpina) | |
| Causa de muerte | Neumonía | |
| Sepultura | Cementerio monumental de Milán | |
| Residencia | Milán | |
| Religión | Catolicismo | |
| Lengua materna | Italiano | |
| Educación | ||
| Educada en | Educación en el hogar | |
| Información profesional | ||
| Ocupación | Filósofa, matemática, filántropa, teóloga y pedagoga | |
| Área | Cálculo infinitesimal, análisis matemático, sección cónica, álgebra, sistema educativo, teología y filosofía | |
| Empleador | Universidad de Bolonia | |
| Orden religiosa | Congregación de la Misión | |
Biografía

Agnesi nació en Milán el 16 de mayo de 1718, fue la primera hija de Pietro Agnesi y Anna Brivio. Se reputa de ser la mayor de 21 hermanos, nacidos de las tres esposas que tuvo su padre. Es considerada una niña prodigio.
No está clara la ocupación de Agnesi, aunque se tiende a descartar su relación con el mundo académico de la Universidad de Bolonia, largamente supuesta, y a considerarlo únicamente una mujer rico de negocios; menos aún se conoce de su madre. Sí es seguro que eran ricos, quizá por el negocio de la seda, y sobre todo ilustrados, y que se esmeraron en la educación de María con medios que --para los que se los pudieran permitir-- eran habituales en la época: preceptores y profesores particulares, y reuniones de intelectuales convocadas en el salón del hogar familiar, en las que se debatían cuestiones filosóficas, especialmente de filosofía natural: cuestiones cercanas a lo que hoy llamamos física.
Aunque estos eventos desagradaban a María Gaetana, de carácter retraído y solitario, el respeto a su padre y sus precoces facultades discursivas, que resaltaban en esos grupos, unidas a las musicales de su hermana María Teresa, hicieron que las sesiones del salón de los Agnesi se hicieran famosas, con un punto de leyenda, por el don de lenguas y la discreción de la hija mayor, con el acompañamiento musical de la menor.
Se atribuye a Agnesi haber adquirido antes de los trece años el dominio del italiano, el latín, el griego, el hebreo, el francés, el español y el alemán. Precocidad y poliglotía son objetivos favoritos de la mitificación, así que según la fuente que se consulte, la edad de referencia puede bajar a los 5 años, y el número y nombre de los idiomas puede oscilar.
Sobre cuánto hay de verdad y cuánto de énfasis de los narradores en la precocidad de María Gaetana, es revelador el ejemplo de su primer ensayo filosófico: algunos quieren que lo redactara en latín a los 9 años, siendo además el asunto tratado la reivindicación del derecho a la educación superior de las mujeres. La historia merece escepticismo, pero tiene detrás realidades sorprendentes, y por supuesto una omisión ornamental: parece que el ensayo existió, su tema era efectivamente la defensa de la formación académica femenina, y la edad de la niña era realmente de 9 años pero se trataba de un ejercicio de traducción propuesto por uno de sus tutores, que había escrito él mismo o tomado de otra fuente el texto original en italiano. María Gaetana lo tradujo al latín, supervisada o no por su tutor, lo memorizó y lo expuso públicamente.
Las descripciones de estas actuaciones de la joven María que nos han dejado algunos testigos sugieren un empeño exhibicionista de su padre, rozando el espectáculo circense. La chica de 20 años que discurría en perfecto latín ("puro, fácil y preciso", "como el de un ángel", dicen los testigos) sobre el origen de las fuentes y los ríos, las mareas, las teorías de Ptolomeo y Newton o la función del hígado, y que venía ofreciendo funciones similares desde los 5 o los 9 años, tenía que sentirse hastiada de su papel. Un visitante pone en su boca: "Lamento haberlo sometido a esto; sé que por cada oyente interesado tengo veinte mortalmente aburridos".
La formación que se administró a María Gaetana en su infancia y juventud tuvo siempre a la religión al lado de la ciencia: los tutores, preceptores e intelectuales contertulios del salón del palacio familiar frecuentemente visten el hábito. Tal ocurre con el jesuita y geómetra Giovanni Saccheri, con el monje y matemático Ramiro Rampinelli, o con el también jesuita y matemático Vincenzo Ricatti (hijo de Jacopo Francesco Ricatti, famoso por la ecuación que lleva su nombre). Era el ambiente que algún autor ha bautizado como "la Ilustración católica".
No es de extrañar entonces que María Gaetana, retraída y solitaria en el fondo, muy religiosa, y con vocación científica, aspire a dejar el mundo y entrar en un convento, como ya había hecho su hermana Giuseppa Teresa. Algunos dicen que una enfermedad de adolescencia reforzó esas convicciones y ese deseo.
La muerte de su madre durante el parto de su octavo hijo da lugar a un pacto entre María Gaetana y su padre. A cambio de no tomar los hábitos, seguir viviendo en casa, y cuidar de él y de sus hermanos, pide a su padre "poder ir a misa siempre que quiera, vestir sencilla y humildemente, y no tener que asistir a bailes y fiestas". Su padre contraerá nupcias otras dos veces, muriendo su segunda esposa tras darle dos hijos, a los que siguieron once de la tercera. Se atribuye a María Gaetana el papel de madre de sus veinte hermanos, la carga correspondiente, y también el dolor que supone perderlos; la mayoría no superaron la infancia, y se dice que solo cuatro superaron los treinta años.
En 1738 Pietro Agnesi pudo publicar un profundo libro de su hija de 20 años, Propositiones Philosóphicae,[1] en el que se compendiaba la defensa de 191 tesis filosóficas debatidas o propuestas en esos encuentros sociales que María Gaetana detestaba.
Travesía en matemáticas
Estudios y legado en matemáticas: Las "Instituzioni"
A partir de los 20 años, Agnesi abandona toda actividad social y se concentra en el estudio de las matemáticas y la religión; su retiro no hubiera sido mayor de haber tomado los hábitos. La gran influencia que tuvo en su formación el monje matemático Ramiro Rampinelli, que había enseñado matemáticas en Roma y en Bolonia, enfatiza ese ambiente científico-monacal que presidió la vida de la matemática italiana. Rampinelli aportó a Agnesi el contacto con los Ricatti, que tuvieron también gran influencia sobre ella; sabemos que Vincenzo se prestó a leer la versión final de las Instituzioni por indicación de su padre, y también que aportó material propio, al que María Gaetana esperó para iniciar la impresión del libro.

En 1748 se publica en Milán la obra más famosa de Agnesi, Instituzioni analítiche ad uso della gioventú italiana, cuya edición ha de costear y realizar ella misma. Sorprendentemente, la imprenta está en la mansión de los Agnesi, y María Gaetana misma dirige los trabajos. El primer tomo está dedicado a las magnitudes finitas, en tanto que el segundo se ocupa del análisis de infinitesimales.[2]
La obra adquiere rápidamente notoriedad entre los matemáticos de la época. Las Instituzioni exponen con claridad los conceptos a través del uso acertado de múltiples ejemplos, y tienen la virtud de armonizar los trabajos, hasta entonces dispersos, de muchos matemáticos, homogeneizándolos en un conjunto único y coherente. Recuérdese que todavía se hablaba de las fluxiones de Newton y de los diferenciales de Leibniz, y que la creación de los símbolos que hoy utilizamos en cálculo, debida sobre todo a Leibniz y a Euler, era muy reciente. Las 1000 páginas de texto y las 50 de ilustraciones resultan sin embargo muy familiares al lector moderno, reflejando el mayor mérito de Agnesi: crear el primer texto completo de Cálculo, desde el álgebra hasta las ecuaciones diferenciales. Superando además tentativas anteriores, singularmente la de L'Hopital en su libro Analyse des infiniment petits.
Se ha destacado del libro el tratamiento de los máximos y mínimos, y se le atribuye haber sido el primer libro de texto que trató conjuntamente el cálculo diferencial y el cálculo integral, explicitando además su naturaleza de problemas inversos, idea que en 1748 no era vieja ni obvia. Se ha elogiado repetidamente la claridad, el orden, la precisión, y el uso afortunado de los ejemplos. Por supuesto, el carácter pionero de la obra implicaba también algunas carencias: las funciones trigonométricas tenían poca presencia (la edición francesa añadió material para corregir esto), y no se trataban las series de potencias, entre otras lagunas.
Entre 1750 y 1752 consta que era catedrática de matemáticas en la Universidad de Bolonia, seguramente de forma honorífica. Durante los cuarenta y siete años siguientes dedicó su vida y hacienda a la caridad y al cuidado de los pobres, ya fuera como residente, como monja de la congregación, o más probablemente como ambas cosas. Este sentido de vocación lo sostuvo hasta encontrar la muerte en el mismo hospicio que había dirigido.
En 1775 la Real Academia de Ciencias publica en París la edición francesa, y en 1801, dos años después de la muerte de María, se publica la inglesa, traducida por John Colson, de Cambridge (tuvo que traducirla bastante antes, porque murió en 1760).[3]
Agnesi también escribió un comentario al Traite analytique des sections coniques, del marqués de L'Hôpital, que lamentablemente nunca fue publicado, pese a que los que tuvieron oportunidad de ver el manuscrito lo consideraron de gran importancia.
En 1786 María tuvo relación con unas obras importantes de Isaac Newton, en una de ellas sobre los principios naturales matemáticos Newton describía la fuerza que hace caer a todos los cuerpos como igual a la fuerza que permite a la luna y a los planetas quedarse en la orbrita.
Curva de Agnesi
Entre los afortunados ejemplos del libro hay uno, al final del primer volumen, que consiguió para María Gaetana Agnesi un lugar en los índices onomásticos de los libros de texto, y en los manuales de fórmulas y tablas matemáticas, y que la ha hecho famosa en mayor medida que todos sus otros méritos: La Curva de Agnesi.
Se trata de una curva que Fermat había estudiado en 163, y para la que Guido Grandi, en 1703, había dado un método de construcción.
Lo de denominar a esta curva como: "bruja", es un error de traducción; solo usan ese término el inglés y las lenguas que han copiado el nombre del inglés. Guido Grandi llamó, en 1718, a la curva versoria en latín, y versiera en italiano. Es un término naval, que identifica la cuerda o cabo que hace girar la vela. María Gaetana Agnesi escribió a su vez la versiera, añadiendo el artículo femenino. John Colson, un traductor de Cambridge con poco conocimiento del italiano, llama a la curva witch ('bruja'), debido a que "confundió" versiera con avversiera (que en italiano significa 'diablesa' o 'demonia'). La dependencia que el idioma español tenía del idioma inglés acabó por embrujarla también en castellano. En otros idiomas se habla de loci (en latín, 'lugares' geométricos, curvas) de Agnesi.
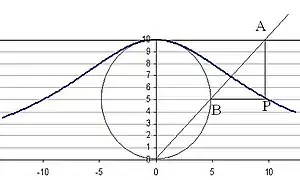
La curva es asintótica al eje X, a la derecha y a la izquierda, y solo se representa por tanto en un entorno del origen, en el que alcanza un máximo justo al cruzar el eje Y. Ese entorno montañoso, y la altura del máximo, vienen determinados por un único parámetro a, que es precisamente la altura del punto máximo alcanzado en x = 0, es decir, el punto (0, a) siempre está en la curva y además es su valor máximo.
El método de construcción es sencillo; para obtener un punto cualquiera de la curva:
- Trácese una circunferencia, con centro en el punto (0, a/2)
- Desde el origen, (0, 0), trácense rectas que crucen con la recta y=a (recta OA en la figura, en la que a=10)
- El punto P de la bruja será aquel en que se crucen las rectas BP (horizontal que pasa por el corte entre OA y la circunferencia) y AP (vertical que pasa por el corte entre OA y la recta y=a).
El conjunto de las rectas OA del plano determina el de los puntos de la curva de Agnesi.
Con un poco de geometría (solo se requieren criterios de igualdad de ángulos, de semejanza de triángulos y el teorema de Pitágoras, más muy poca álgebra) se demuestra que la ecuación de la bruja de Agnesi es:
Y las ecuaciones paramétricas son:
Agnesi no presenta ecuaciones paramétricas, pese a que el tratamiento hubiera sido más sencillo, a través de:
Contribuciones principales
Para la historia de las matemáticas Agnesi es importante por su influencia en la divulgación del cálculo. También es uno de los personajes más citados en las reflexiones sobre el papel histórico de la mujer en la matemática: basta considerar que las Instituzioni analítiche son según algunos la obra matemática de autoría femenina más antigua que se conserva.[4][5]
Su nombre está a veces en el índice de los libros de geometría analítica y de cálculo, siempre asociado a la curva llamada indebidamente: "bruja", Curva de Agnesi. Los dos sustantivos son inciertos: Agnesi no descubrió esa curva, ni lo pretendió, y el nombre de "bruja" seguramente lo aportó el azar una mala traducción al inglés, que así apareció también en español.[6]
Muchas de sus obras fueron traducidas al inglés y francés, las Instituzioni tuvieron gran impacto en la enseñanza, pues armonizaban, en un discurso único, materiales dispersos y heterogéneos de matemáticos anteriores, mostrando por primera vez una secuencia lógica y didáctica desde el álgebra hasta las ecuaciones diferenciales.[5] En la Biblioteca Ambrosiana de Milán se guardan sus obras inéditas que ocupan veinticinco volúmenes.[7]
Trayectoria religiosa
En 1750 el padre de María enferma gravemente, y ella es designada por el papa Benedicto XIV para la cátedra de matemáticas y filosofía natural de la Universidad de Bolonia. Entre 1750 y 1752 ejerce la cátedra, seguramente de forma honorífica.[8]
Pietro Agnesi muere en 1752, y a partir de ese momento María se da al estudio de la Teología, al parecer especialmente de la Patrística, dedica su fortuna a obras de caridad, terminando en la miseria, ejerce desde 1771 por designación del arzobispo Tozzobonelli como directora del Hospicio Trivulzio de Milán, se concentra en el cuidado de los menesterosos y enfermos, sobre todo mujeres mayores, y muere ella misma en la institución que dirigía, el 9 de enero de 1799.
Las incertidumbres y la leyenda la acompañan hasta la muerte: unos sugieren que si murió en el Hospicio Trivulzio es porque sus donaciones la habían sumido en la pobreza, y era ahora una residente menesterosa más. Otros sostienen que había cumplido por fin sus deseos, y era monja agustiniana (o "monja azul", por el color del hábito) del hospicio.
Bibliografía
- Mazzotti, Massimo (2007). The world of Maria Gaetana Agnesi, mathematician of God. Baltimore: Johns Hopkins University Press.
- — (2001). “Maria Gaetana Agnesi: Mathematics and the Making of the Catholic Enlightenment”, Isis 92(4):657-683, diciembre de 2001 (disponible en línea.
Referencias
- Agnesi, Maria Gaetana (1738). Propositiones philosophicae (en latin). In Curia Regia, per Joseph Richinum Malatestam ... Consultado el 23 de agosto de 2017.
- Barcelona, EL PERIÓDICO / (16 de mayo de 2014). «Google dedica su 'doodle' a la matemática y filósofa María Gaetana». elperiodico (en español). Consultado el 23 de agosto de 2017.
- En Google libros puede consultarse un facsímil del volumen I de la traducción de Colson, Analytical Institutions
- «María Gaetana Agnesi». www.quien.net. Consultado el 7 de agosto de 2017.
- «Apuntes de ciencia: Gaetana Agnesi, filósofa y matemática (1718-1799) | En la red». Mujeres con ciencia. 28 de noviembre de 2014. Consultado el 7 de agosto de 2017.
- «¿Descubrió realmente Maria Gaetana Agnesi la «curva de la bruja»?». La Voz de Galicia. 16 de mayo de 2014. Consultado el 23 de agosto de 2017.
- «María Gaetana Agnesi (1718-1799) | Vidas científicas». Mujeres con ciencia. 11 de julio de 2017. Consultado el 7 de agosto de 2017.
- «Maria Gaetana Agnesi, la bruja matemática que cambió el cálculo con su curva, en el doodle de Google». Las Provincias. Consultado el 23 de agosto de 2017.
Enlaces externos
 Wikimedia Commons alberga una galería multimedia sobre María Gaetana Agnesi.
Wikimedia Commons alberga una galería multimedia sobre María Gaetana Agnesi.- Maria Gaetana Agnesi en Divulgamat Centro virtual de divulgación de las matemáticas. Biografía de María Molero Aparicio y Adela Salvador Alcaide.
- Ficha en la NNDB