Número de la suerte

En la teoría de números, un número de la suerte es un número natural en un conjunto que se genera utilizando un sistema de criba similar a la Criba de Eratóstenes utilizada para generar los números primos.[1]

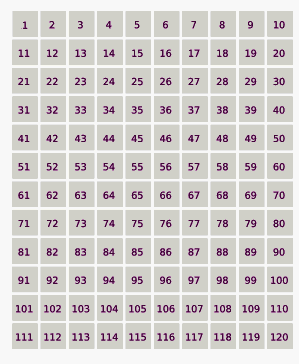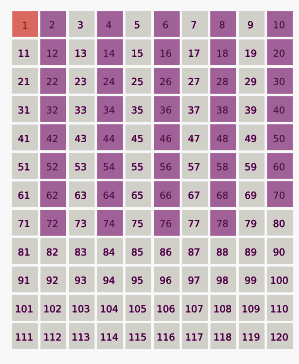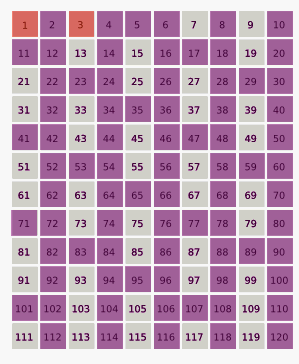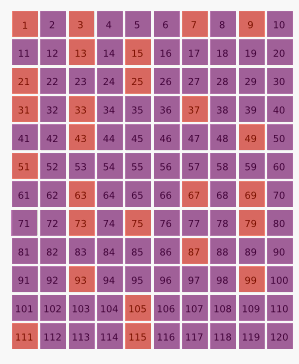
Una animación demostrando cuales son los números de la suerte (los marcados en rojo)

Comenzando con una lista de números enteros a partir de 1:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25...

Se eliminan los números de dos en dos, todos los números pares; en esta primera iteración solo quedan los números impares:

1,    3,    5,    7,    9,     11,     13,     15,     17,     19,     21,     23,     25...

El segundo término de esta secuencia es 3. Entonces se eliminan todos los números restantes de tres en tres:

1,    3,          7,    9,             13,     15,             19,     21,             25...

El tercer número que ha quedado es 7, así que cada séptimo número que queda se elimina:

1,    3,          7,    9,             13,     15,                     21,             25...

Dado que este procedimiento se repite indefinidamente, los sobrevivientes son los números de la suerte:[1]

1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99...

El término fue introducido en 1955 en un artículo de Gardiner, Lazarus, Metropolis y Ulam, que también sugirieron que la criba con la que se obtienen los números de la suerte, se debería llamar, Criba de Josefo Flavio.[2]

Los números de la suerte comparten algunas propiedades con los números primos, como el comportamiento asintótico de acuerdo con el teorema de los números primos, también se les ha extendido la conjetura de Goldbach.

Al igual que los números primos, hay infinitos números de la suerte y debido a las conexiones evidentes entre los dos grupos, algunos matemáticos han sugerido que estas propiedades se pueden encontrar en una clase más amplia de conjuntos de números generados por cribas, aunque hay pocas bases teóricas para esta conjetura.

Una de estas similitudes son los números de la suerte gemelos, que ocurren con una frecuencia similar a los primos gemelos.

Otro grupo destacable son los números primos de la suerte, números que son a la vez primos y de la suerte, no se sabe aún si es un grupo infinito, los primeros son:[3]

3, 7, 11, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193

Referencias
  1. The OEIS Foundation, Inc. (Marzo de 2008). «Secuencia de Números de la suerte». The On-Line Encyclopedia of Integer Sequences. Consultado el 21 de julio de 2010.
  2. V. Gardiner, R. Lazarus, N. Metropolis and S. Ulam, "On certain sequences of integers defined by sieves", Mathematics Magazine 29:3 (1955), pp. 117–122.
  3. The OEIS Foundation, Inc. (Marzo de 2008). «Secuencia de Números primos de la suerte». The On-Line Encyclopedia of Integer Sequences. Consultado el 21 de julio de 2010.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.