NP-completo

En teoría de la complejidad computacional, la clase de complejidad NP-completo es el subconjunto de los problemas de decisión en NP tal que todo problema en NP se puede reducir en cada uno de los problemas de NP-completo. Se puede decir que los problemas de NP-completo son los problemas más difíciles de NP y muy probablemente no formen parte de la clase de complejidad P. La razón es que de tenerse una solución polinómica para un problema NP-completo, todos los problemas de NP tendrían también una solución en tiempo polinómico.

Si se demostrase que un problema NP-completo, llamémoslo A, no se pudiese resolver en tiempo polinómico, el resto de los problemas NP-completos tampoco se podrían resolver en tiempo polinómico. Esto se debe a que si uno de los problemas NP-completos distintos de A, digamos X, se pudiese resolver en tiempo polinómico, entonces A se podría resolver en tiempo polinómico, por definición de NP-completo. Ahora, pueden existir problemas en NP y que no sean NP-completos para los cuales exista solución polinómica, aun no existiendo solución para A.

Como ejemplo de un problema NP-completo encontramos el problema de la suma de subconjuntos que se puede enunciar como sigue: dado un conjunto S de enteros, ¿existe un subconjunto no vacío de S cuyos elementos sumen cero? Es fácil verificar si una respuesta es correcta, pero no se conoce mejor solución que explorar todos los 2n-1 subconjuntos posibles hasta encontrar uno que cumpla con la condición.

Definición de NP-completo

Un problema de decisión C es NP-completo si:

  1. C está contenido en el conjunto NP, y
  2. Todo problema de NP es reducible a C en tiempo polinomial.

Se puede demostrar que C es NP demostrando que un candidato a solución de C puede ser verificado en tiempo polinómico.

Una transformación polinómica de L en C es un algoritmo determinista que transforma instancias de l ∈ L en instancias de c ∈ C, tales que la respuesta a c es positiva si y sólo si la respuesta a l lo es.

Como consecuencia de esta definición, de tenerse un algoritmo en P para C, se tendría una solución en P para todos los problemas de NP.

Esta definición fue propuesta por Stephen Cook en 1971. Al principio parecía sorprendente que existieran problemas NP-completos, pero Cook demostró (teorema de Cook) que el problema de satisfacibilidad booleana es NP-completo. Desde entonces se ha demostrado que miles de otros problemas pertenecen a esta clase, casi siempre por reducción a partir de otros problemas para los que ya se había demostrado su pertenencia a NP-completo; muchos de esos problemas aparecen en el libro de Garey and Johnson's de 1979 Computers and Intractability: A Guide to NP-completeness.

Un problema que satisface la segunda condición pertenece a la clase NP-hard independientemente de que satisfaga la primera.

Historia

El concepto de "NP-completo" fue introducido por Stephen Cook en un artículo titulado 《The complexity of theorem-proving procedures》 en las páginas 151-158 de Proceedings of the 3rd Annual ACM Symposium on Theory of Computing en 1971, aunque el término "NP-completo" como tal no aparece en el documento. En la conferencia de ciencias de la computación hubo un intenso debate entre los científicos de la computación sobre si los problemas NP-completos podían ser resueltos en tiempo polinómico o en una máquina de Turing determinista. John Hopcroft llevó a todos los asistentes de la conferencia a consenso concluyendo que el estudio sobre si los problemas NP-completos son resolubles en tiempo polinómico debería ser pospuesto ya que nadie había conseguido probar formalmente sus hipótesis ni en un sentido ni en otro. Esto se conoce como el problema ¿P=NP?.

Nadie ha sido capaz aún de dar una respuesta final a este problema, haciéndolo uno de los grandes problemas no resueltos de la matemática. Desde mayo de 2000, el Clay Mathematics Institute ofrece una recompensa de un millón de dólares a quien logre dar una demostración de que P=NP o P≠NP.

El Teorema de Cook demuestra que el problema de satisfacibilidad booleana es un problema NP-completo. En 1972, Richard Karp demostró que otros problemas eran también NP-completos (ver Lista de 21 problemas NP-completos de Karp). A partir de los resultados originales del Teorema de Cook, se han descubierto cientos de problemas que también pertenecen a NP-completo mediante reducciones desde otros problemas que previamente se habían demostrado NP-completos; muchos de estos problemas han sido recogidos en libro de 1979 de Garey and Johnson's Computers and Intractability: A Guide to NP-Completeness.

Ejemplos

Un problema interesante en teoría de grafos es el de isomorfismo de grafos: Dos grafos son isomorfos si se puede transformar uno en el otro simplemente renombrando los vértices. De los dos problemas siguientes:

Isomorfismo de grafos: ¿Es el grafo G1 isomorfo al grafo G2?
Isomorfismo de subgrafos: ¿Es el grafo G1 isomorfo a un subgrafo del grafo G2?

Se sospecha que el problema de isomorfismo de grafos no está ni en P ni en NP-completo, aunque está en NP. Se trata de un problema difícil, pero no tanto como para estar en NP-completo.

La forma más sencilla de demostrar que un nuevo problema es NP-completo es: primero demostrar que está en NP y luego transformar a este, en tiempo polinómico, en un problema que ya esté en NP-completo. Para ello resulta útil conocer algunos de los problemas de los que existe prueba de pertenencia a NP-completo. Algunos de los más famosos son:

Véase también:

  • Categoría:Problemas NP-completos
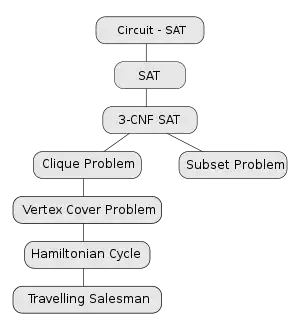
Algunos problemas NP-completos, indicando las reducciones usadas típicamente de completitud NP

A la derecha, un diagrama de algunos de los problemas y sus reducciones típicamente usadas para demostrar su completitud NP. En este diagrama, una flecha de un problema a otro indica la dirección de la reducción. Nótese que este diagrama puede resultar engañoso al llevarnos a pensar que muestra una descripción de la relación matemática entre esos problemas, ya que existe una relación de reducción de tiempo polinómico entre dos problemas NP-completos cualesquiera; pero esto indica que demostrar estas reducciones de tiempo polinómicas ha sido más fácil.

A menudo hay solo una pequeña diferencia entre un problema P y uno NP-completo. Por ejemplo, el problema 3SAT, una restricción del problema de satisfacibilidad, sigue siendo NP-completo, mientras que el problema 2SAT -ligeramente más estricto- está en P (específicamente, NL-completo), y el problema MAX 2SAT -ligeramente más general- es, de nuevo, NP-completo. Determinar si un grafo puede ser coloreado con 2 colores, está en P, pero con tres colores es NP-completo, incluso cuando se restringe a los grafos planos. Determinar si un grafo es ciclo o es bipartito es muy fácil (en L), pero encontrar un subgrafo máximo bipartito o ciclo es NP-completo. Una solución del problema de la mochila (knapsack) dentro de cualquier porcentaje fijo de la solución óptima puede ser computado en tiempo polinómico, pero encontrar la solución óptima es NP-completo.

Soluciones aproximadas

Actualmente, todos los algoritmos conocidos para problemas NP-completos utilizan tiempo exponencial con respecto al tamaño de la entrada. Se desconoce si hay algoritmos más rápidos, por lo cual, para resolver un problema NP-completo de tamaño arbitrario, se utiliza uno de los siguientes enfoques:

  • Aproximación: Un algoritmo que rápidamente encuentra una solución no necesariamente óptima, pero dentro de un cierto rango de error. En algunos casos, encontrar una buena aproximación es suficiente para resolver el problema, pero no todos los problemas NP-completos tienen algoritmos de aproximación.
  • Probabilístico: Un algoritmo probabilístico utiliza aleatoriedad para obtener en promedio una buena solución al problema planteado con una pequeña probabilidad de fallar, para una distribución de los datos de entrada dada.
  • Restricciones: Restringiendo la estructura de las entradas se pueden encontrar algoritmos más rápidos.
  • Casos particulares: Puede ocurrir que se reconozcan casos particulares del problema para los cuales existen soluciones rápidas.
  • Algoritmo genético: Algoritmos que mejoran las posibles soluciones hasta encontrar una que posiblemente esté cerca del óptimo. Tampoco existe forma de garantizar la calidad de la respuesta.
  • Heurísticas: Un algoritmo que trabaja razonablemente bien en muchos casos. En general son rápidos, pero no existe medida de la calidad de la respuesta. Las aproximaciones metaheurísticas suelen ser empleadas.

Un ejemplo de algoritmo heurístico de complejidad O(n log n) es el algoritmo voraz utilizado para la coloración de vértices en algunos compiladores. Gracias a que la mayoría de máquinas RISC tienen un gran número de registros de propósito general, incluso una aproximación heurística es efectiva para esta aplicación.

Completitud bajo diferentes tipos de reducción

En la definición de NP-completo dada anteriormente, el término "reducción" fue utilizado en el sentido transformar las instancias de un problema en instancias de otro (reducciones many-one).

Otro tipo de reducción consiste en la "reducción en tiempo polinómico de Turing". Un problema X es reducible en tiempo polinómico de Turing Y si dada una función que resuelve Y en tiempo polinómico, podría escribirse un programa que llamando a la subrutina anterior resuelva X en tiempo polinómico. Esto contrasta con el uso del término reducción del que hablábamos al principio ya que este tiene la restricción de que el programa solamente puede llamar una vez al subalgoritmo y el valor retornado por este debe ser el valor de retorno del programa.

Si se definen el análogo a NP-completo con reducciones de Turing en lugar de reducciones many-one, el conjunto de problemas resultante no sería menor de NP-completo, de hecho se cuestiona si serían más grandes. Si los dos conceptos fuesen lo mismo, se seguiría que NO = Co-NP. Esto se mantiene porque por definición las clases de los problemas NP-completos y co-NP-completos bajo las reducciones de Turing son las mismas gracias a que las clases definidas con reducciones many-one son subclases de estas mismas. Por lo tanto si ambas definiciones de la NP-completitud son iguales hay un problema co-NP-completo (bajo ambas definiciones) como por ejemplo el complementario del problema de la satisfacibilidad booleana que es también NP-completo (bajo ambas definiciones). Esto implica que NP = co-NP como se muestra como prueba en el artículo sobre co-NP. Aunque la cuestión de si NP = co-NP es una pregunta abierta se considera muy poco probable porque también es muy poco probable que las dos definiciones de NP-completitud sean equivalentes.

Otro tipo de reducción es empleado frecuentemente para definir NP-completitud es la de reducción de espacio logarítmico many-one que puede ser computerizada empleando únicamente una cantidad logarítmica de espacio. Ya que cada computación que puede ser realizada en espacio logarítmico también puede ser realizada en tiempo polinomial se razona que si hay una reducción de espacio logarítmico many-one también hay una reducción de tiempo polinómico many-one. Este tipo de reducción es más refinada que la más usual reducción de tiempo polinómico many-one y permite distinguir más clases como la P-completa. Ya sea en virtud de estos tipos de reducciones los cambios en la definición de NP-completo son todavía un problema abierto.

Véase también

Referencias
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.