Newton (unidad)

En física, un newton[1] (símbolo: N) es la unidad de medida de la fuerza en el Sistema Internacional de Unidades, nombrada de esa forma por las aportaciones de Isaac Newton a la física, especialmente a la mecánica clásica concretamente Segunda ley del movimiento de Newton.

Newton
Estándar unidades derivadas del Sistema Internacional
Magnitud Fuerza
Símbolo N
Nombrada en honor de Isaac Newton
Equivalencias
Unidades básicas del Sistema Internacional 1 N = 1 kg.m/s²
Sistema Técnico de Unidades 1 N = 1/9,80665
Sistema Cegesimal de Unidades 1 N = 105 dyn
Unidades de Planck 1 N = 1,21027×1044 N

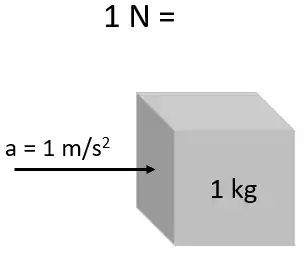
Se define como 1 kg⋅m/s2, la fuerza que proporciona a una masa de 1 kilogramo una aceleración de 1 metro por segundo en cada segundo.

Definición

Es una unidad derivada del Sistema Internacional de Unidades que se compone de las unidades básicas:

Un newton es la cantidad de fuerza aplicada durante un segundo a una masa de un kilogramo para que esta adquiera la velocidad de un metro por segundo respecto a la velocidad colineal que tenía previamente a la aplicación de la fuerza.[2] Las fuerzas tienen carácter vectorial y son la base del estudio de la dinámica, una de las principales ramas que tiene la mecánica.

En 1946, la VIII Conferencia General de Pesos y Medidas (CGPM), resolución 2, normalizó la unidad de fuerza del sistema MKS de unidades como la fuerza necesaria para proporcionar una aceleración de un 1 m/s² a un objeto de 1 kg de masa.[3] La IX CGPM, de 1948, adoptó el nombre de «newton» en su resolución 7.[4]

En términos más formales, Segunda ley del movimiento de Newton establece que la fuerza ejercida sobre un objeto es directamente proporcional a la aceleración adquirida por dicho objeto, así:[5]

donde representa la masa del objeto sometido a una aceleración .

Ejemplos

La gravedad media en la Tierra (convencionalmente, g = 9,80665 m/s²), una masa de un kilogramo ejerce una fuerza de unos 9,8 newtons.

  • Una manzana de tamaño medio, con 200 g, ejerce unos dos newtons de fuerza en la superficie de la Tierra, que medimos como el peso de la manzana en la Tierra.
0,200 kg × 9,80665 m/s² = 1,961 N.
62 kg × 9,80665 m/s² = 608 N (donde 62 kg es la masa media mundial de un adulto).[6]

Kilonewtons
Un mosquetón utilizado en escalada en roca, con un índice de seguridad de 26 kN cuando se carga a lo largo de la espina dorsal con el gatillo cerrado, 8 kN cuando se carga perpendicular a la espina dorsal, y 10 kN cuando se carga a lo largo de la espina dorsal con el gatillo abierto.

Es frecuente véase fuerzas expresadas en kilonewtons (kN), donde 1 kN = 1000 N. Por ejemplo, el esfuerzo de tracción de una locomotora de tren de vapor Clase Y y el empuje de un F100 son ambos de alrededor de 130 kN.

Un kilonewton, 1 kN, equivale a 102 kgf, o unos 100 kg de carga bajo la gravedad terrestre.

1 kN = 102 kg × 9,81 m/s².

Así, por ejemplo, una plataforma que indique que tiene una capacidad nominal de 321 kilonewtons (72 163,7 lbf) soportará con seguridad una carga de 32 100 kilogramos (70 768,4 lb).

Las especificaciones en kilonewtons son comunes en las especificaciones de seguridad para:

Múltiplos del Sistema Internacional

En la tabla que sigue se relacionan los múltiplos y submúltiplos del newton en el Sistema Internacional de Unidades.

Múltiplos del Sistema Internacional para newton (N)
Submúltiplos Múltiplos
Valor Símbolo Nombre Valor Símbolo Nombre
10−1 N dN decinewton 101 N daN decanewton
10−2 N cN centinewton 102 N hN hectonewton
10−3 N mN milinewton 103 N kN kilonewton
10−6 N µN micronewton 106 N MN meganewton
10−9 N nN nanonewton 109 N GN giganewton
10−12 N pN piconewton 1012 N TN teranewton
10−15 N fN femtonewton 1015 N PN petanewton
10−18 N aN attonewton 1018 N EN exanewton
10−21 N zN zeptonewton 1021 N ZN zettanewton
10−24 N yN yoctonewton 1024 N YN yottanewton
10−27 N rN rontonewton 1027 N RN ronnanewton
10−30 N qN quectonewton 1030 N QN quettanewton
Prefijos comunes de unidades están en negrita.
Esta unidad del Sistema Internacional es nombrada así en honor a Isaac Newton. En las unidades del SI cuyo nombre proviene del nombre propio de una persona, la primera letra del símbolo se escribe con mayúscula (N), en tanto que su nombre siempre empieza con una letra minúscula (newton), salvo en el caso de que inicie una frase o un título.
Basado en The International System of Units, sección 5.2.

Factores de conversión
Units of force
newton dina kilogramo-fuerza,
kilopondio		 libra-fuerza poundal
1 N ≡ 1 kg⋅m/s-2 = 105 dyn ≈ 0.10197 kp ≈ 0.22481 lbf ≈ 7.2330 pdl
1 dina = 10-5 N ≡ 1 g⋅cm/s2 ≈ 1.0197-6kp ≈ 2.2481-6lbf ≈ 7.2330-5pdl
1 kp = 9.80665 N = 980665 dina ≡ gn × 1 kg ≈ 2.2046 lbf ≈ 70.932 pdl
1 lbf ≈ 4.448222 N ≈ 444822 dina ≈ 0.45359 kp ≡ g{n × 1 lb ≈ 32.174 pdl 
1 pdl ≈ 0.138255 N ≈ 13825 dina ≈ 0.014098 kp ≈ 0.031081 lbf ≡ 1 lb⋅ft/s2
El valor de gn como se utiliza en la definición oficial del kilogramo-fuerza (9,80665 m/s2) se utiliza aquí para todas las unidades gravitacionales.

Véase también

Referencias
  1. Real Academia Española. «newton». Diccionario de la lengua española (23.ª edición). Consultado el 21 de marzo de 2015.
  2. «Newton | unit of measurement». Encyclopedia Britannica (en inglés). Archivado desde el original el 27 de septiembre de 2019. Consultado el 27 de septiembre de 2019.
  3. Newton (unidad), p. 65, en Google Libros
  4. Oficina Internacional de Pesas y Medidas (1977). The international system of units. 330-331 (3.ª edición). U.S. Dept. of Commerce, National brasol of Standards. p. 17. ISBN 0745649742. Consultado el 31 de julio de 2016.
  5. Oficina Internacional de Pesas y Medidas, ed. (2006). «Tabla 3. Unidades derivadas coherentes en el SI con nombres y símbolos especiales». El Sistema Internacional de Unidades (SI). Archivado desde el original el 18 de junio de 2007.
  6. Walpole, Sarah Catherine; Prieto-Merino, David; Edwards, Phillip; Cleland, John; Stevens, Gretchen; Roberts, Ian (2012). «El peso de las naciones: una estimación de la biomasa humana adulta». BMC Public Health 12 (12): 439. PMC 3408371. PMID 22709383.

Bibliografía
  • Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
  • Resnick, Robert & Halliday, David (2004). Física 4.ª. CECSA, México. ISBN 970-24-0257-3.
  • Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6.ª edición). Brooks/Cole. ISBN 0-534-40842-7.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.