Nefroide
La nefroide es una curva plana cuyo nombre significa forma de riñón. Aunque el término nefroide fue usado para describir otras curvas, fue aplicado para esta por Richard Anthony Proctor (1837-1888), matemático inglés que en 1878 publicó The geometry of cycloids en Londres. Christiaan Huygens (1629-1695), en 1678, demostró que la nefroide es la catacáustica de un círculo cuando el rayo de luz está en el infinito. Publicó esto en el Traité de la lumiére en 1690. (Una explicación del porqué no se descubrió hasta que se conoció la teoría de la longitud de onda del rayo de luz; se demostró teóricamente en 1838).
Este tipo de curvas fue estudiado además por Tschirnhausen en 1679, Jacques Bernoulli en 1692, Daniel Bernoulli en 1725 y Proctor, que como se ha mencionado le dio nombre en 1878.
Definición
La nefroide es una epicicloide de dos puntos de retroceso cuya forma es la de un riñón. Es engendrada por una circunferencia de radio que gira exteriormente sin deslizar sobre una circunferencia de radio y de centro .[1]
Ecuaciones de la nefroide
Ecuaciones paramétricas

Ecuaciones paramétricas para la nefroide mostrada a la derecha, con picos en el eje y, vienen dadas por:
Cuando los picos están en el eje x, las ecuaciones paramétricas están dadas por:
Ecuación cartesiana
Una ecuación cartesiana para la nefroide sería:
Propiedades de la nefroide
Las propiedades hacen referencia a la nefroide parametrizada por el primer par de ecuaciones mencionadas antes. La longitud de arco y el área de la nefroide son, respectivamente,
El radio de curvatura está dado por
Generación de la nefroide
La nefroide piuede generarse de varios modos:
- cáustica de un círculo: la nefroide puede verse como una cáustica de un círculo para los rayos proyectados desde un foco exterior a la circunferencia. En otras palabras, si un círculo refleja rayos paralelos de luz, el rayo reflectado nos daría una nefroide. En el vídeo, el rayo incidente se muestra en amarillo y los rayos reflejados en marrón. La nefroide aparece como la envolvente del haz de rayos reflejados.
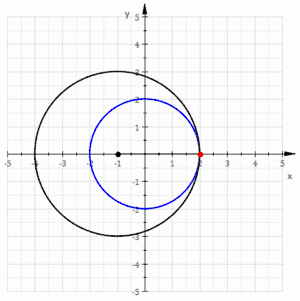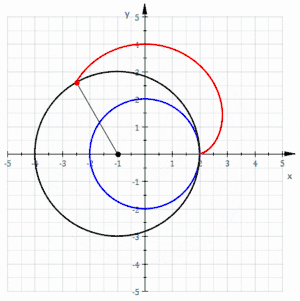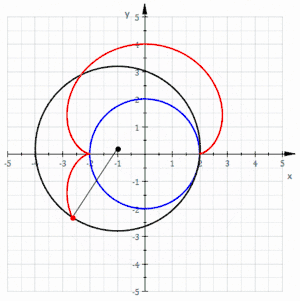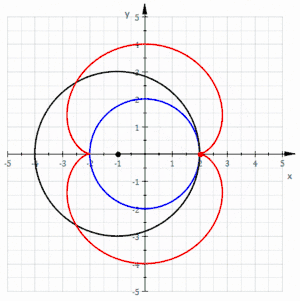
- envolvente de círculos: una nefroide puede crearse como una envolvente de círculos. Como se ve en la figura de la izquierda, se empieza con un círculo base (azul), y después se selecciona un punto en ese círculo (punto rojo). Con ese punto como centro, se dibuja un círculo (rojo) tangente al eje y. Cuando se dibujan varios círculos de esta forma, se produce la imagen de una nefroide.
- envolvente de líneas: una nefroide puede crearse como una envolvente de líneas. Se empieza con un círculo de radio a. Para varios valores de t, se unen los puntos que están a t grados y a 3t grados alrededor del círculo. En otras palabras, hay que unir los puntos y Estas líneas envuelven a la nefroide.
- epicicloide de dos picos: la nefroide es también una epicicloide de dos picos. En la figura, el círculo azul pequeño de radio a es tangente exterior del círculo mayor de radio 2a. Según el círculo pequeño va rodando a lo largo del círculo mayor sin deslizar, de forma que los dos arcos rojos son siempre de la misma longitud, el punto verde traza la nefroide.
- Generación de la nefroide
- Nefroide formada al proyectar rayos de luz desde un foco exterior a una circunferencia
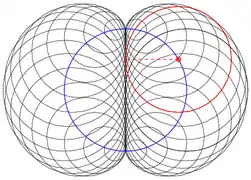 Nefroide como envolvente de círculos
Nefroide como envolvente de círculos- Nefroide utilizando GeoGebra mediante circunferencias tangentes (rojo) a un diámetro de una circunferencia mayor (azul) (hay 36 círculos con centros espaciados 10º sobre el círculo base)
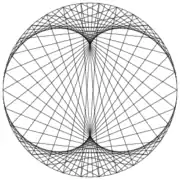 Nefroide como envolvente de líneas (90 líneas correspondientes al parámetro t tomando como valores los múltiplos de 4)
Nefroide como envolvente de líneas (90 líneas correspondientes al parámetro t tomando como valores los múltiplos de 4)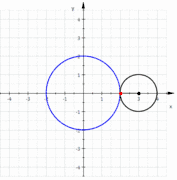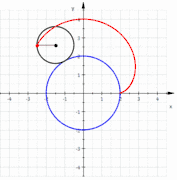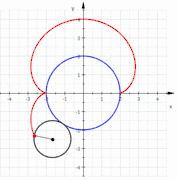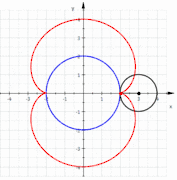 Nefroide como epicicloide de dos picos (línea roja): el círculo azul de radio 3 a es tangente interior al círculo negro de radio 2a. Según el círculo mayor rueda alrededor del pequeño sin deslizar, de forma que los dos arcos rojos son siempre de la misma longitud, el punto verde traza una nefroide.
Nefroide como epicicloide de dos picos (línea roja): el círculo azul de radio 3 a es tangente interior al círculo negro de radio 2a. Según el círculo mayor rueda alrededor del pequeño sin deslizar, de forma que los dos arcos rojos son siempre de la misma longitud, el punto verde traza una nefroide.
Curvas derivadas de la nefroide
- Evoluta: la evoluta de la nefroide es otra nefroide de la mitad de tamaño y girada 90 grados. La nefroide original es así vista como una envolvente de sus círculos osculadores (gris). 2 círculos osculadores pueden verse en azul. Sus centros aparecen sobre la evoluta (nefroide roja pequeña:).
- involuta: como la involuta de una nefroide es otra nefroide, se tiene que la involuta de la nefroide también es otra nefroide. La nefroide original (envolvente de círculos grises) en la imagen previa, es la involuta de la nefroide roja más pequeña.
- inversa: La inversa con respecto al origen de la nefroide (en rojo) es la curva mostrada como la envolvente de círculos (en negro). Estos círculos son los inversos de aquellos que servían en una imagen anterior para describir la nefroide como una envolvente de círculos. Al invertir respecto a un círculo de radio a, una ecuación cartesiana para la inversa es
- Derivadas de la nefroide
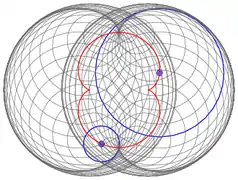 Evoluta de la nefroide (hay 60 círculos correspondientes al parámetro t tomando como valores los múltiplos de 6.)
Evoluta de la nefroide (hay 60 círculos correspondientes al parámetro t tomando como valores los múltiplos de 6.)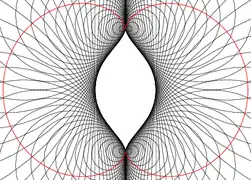 Inversa de la nefroide
Inversa de la nefroide
Referencias
- Curvas en la historia, de José Manuel Álvarez Pérez
- Julián Espinoza de los Montesinos Diccionario de matemáticas ISBN 84-8055-355-3
Enlaces externos
- Weisstein, Eric W. «Nephroid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.