Nonio
El nonio[1] [2] [3] o escala de Vernier[4][5] es una segunda escala auxiliar que tienen algunos instrumentos de medición, que permite apreciar una medición con mayor exactitud al complementar las divisiones de la regla o escala principal del instrumento de medida.[6]

Historia
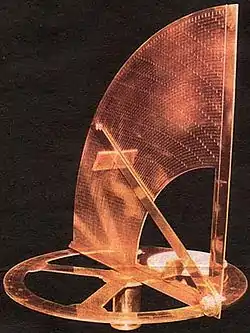
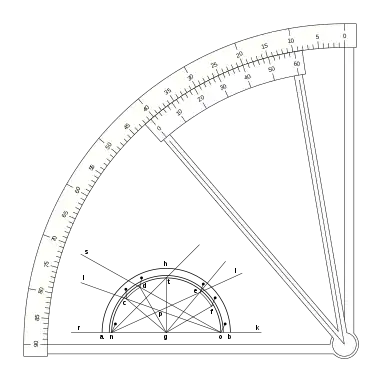
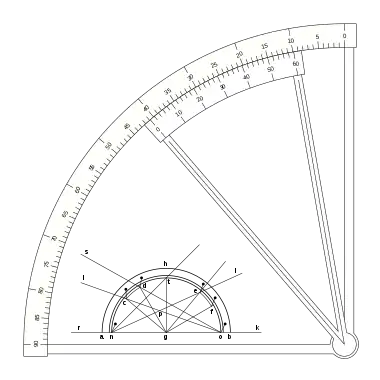
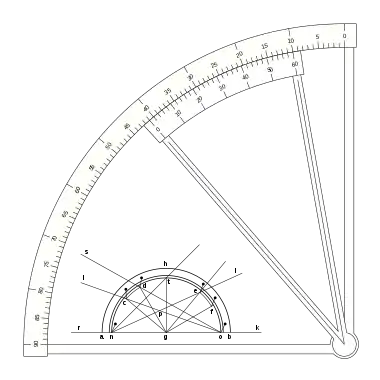
Pedro Nunes, conocido también por su nombre latino como Petrus Nonius (Alcácer do Sal, Portugal, 1492 – Coímbra, 1577), matemático, astrónomo y geógrafo portugués del siglo XVI, inventó en 1514 el nonio: un dispositivo de medida de longitudes que permite —con la ayuda de un astrolabio— medir fracciones de grado de ángulo.
El astrolabio de Pedro Nunes consistía en una serie de escala paralelas, de modo que alguna de ellas coincidiera lo más exactamente posible con la medición efectuada
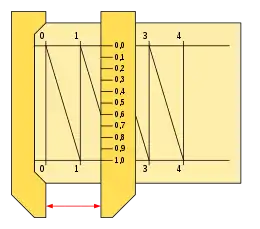
La escala transversal se usó en un momento en que los instrumentos finamente graduados eran difíciles de construir. Se han encontrado escalas transversales en instrumentos construidos a principios del siglo XIV, se desconoce el inventor, aunque se sabe que Leví ben Gerson las utilizó en su Vara de Jacob.[7][8] (aparentemente inventada el siglo anterior por Jacob ben Makira) y describió el método de la escala transversal aplicado a dicho instrumento.
Thomas Digges atribuyó, erróneamente, el descubrimiento de la escala transversal al navegante y explorador Richard Chancellor (citado por algunos como relojero y con otros nombres como Richard Chansler o Richard Kantzler).[9][10][11][12][13][14] Su uso en instrumentos astronómicos se popularizó a finales del siglo XVI. Tycho Brahe las utilizó y consiguió popularizar la técnica.[15] Finalmente el sistema comenzó a morir una vez que el nonius se hizo común a finales del siglo XVIII - más de un siglo después de que Pierre Vernier introdujera la técnica.[16]
Pierre Vernier (Ornans, 1580 – ibídem, 1637), matemático francés, es conocido por la invención en 1631 de la escala Vernier[17] para medir longitudes con gran precisión, recogida en su obra: La Construction, l'usage et les propriétez du quadrant nouveau de mathematique publicada en el año: 1631.[18] [19]
Dada la primera invención de Pedro Nunes (1514) y el posterior desarrollo de Pierre Vernier (1631), en la actualidad esta escala se suele denominar como «nonio» o «vernier», siendo empleado uno u otro término en distintos ambientes. En la rama técnica industrial suele ser más utilizado «nonio», si bien el término «vernier» es común en la enseñanza y en las ciencias aplicadas. Tomaremos el término «nonio» al ser el más antiguo y por tanto el que aportó la idea original, considerando, en todo caso, «nonio» y «vernier» como términos sinónimos.
Principio de funcionamiento
El sistema consiste en una regla sobre la que se ha grabado una serie de divisiones según el sistema de unidades empleado, y una corredera o carro móvil, con un fiel o punto de medida, que se mueve a lo largo de la regla.
 |
 |
 |
 |
 |
 |
 |
 |
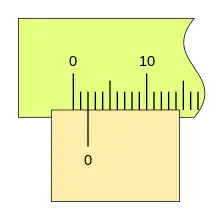 |
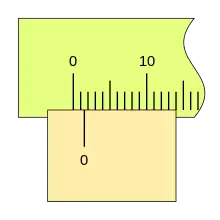
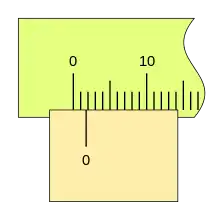
En una escala de medida, podemos apreciar hasta su unidad de división más pequeña, siendo esta la apreciación con la que se puede dar la medición; es fácil percatarse de que entre una división y la siguiente hay más medidas, que unas veces están más próximas a la primera de ellas y otras a la siguiente.
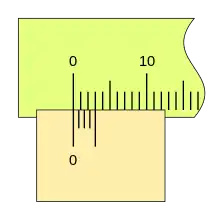
Para poder apreciar distintos valores entre dos divisiones consecutivas, se ideó una segunda escala que se denomina nonio o vernier. Grabada sobre la corredera y cuyo punto cero es el fiel de referencia. El nonio o vernier es esta segunda escala, no el instrumento de medida o el tipo de medida a realizar, tanto si es una medición lineal, angular, o de otra naturaleza, y sea cual fuere la unidad de medida. Esto es, si empleamos una regla para hacer una medida, solo podemos apreciar hasta la división más pequeña de esta regla; si además disponemos de una segunda escala, llamada nonio o vernier, podemos distinguir valores más pequeños.
El nonio o escala vernier toma un fragmento de la regla y lo divide en un número más de divisiones. En la figura se toman 3 divisiones de la regla y la dividen en 4 partes iguales; como caso más sencillo para ver el principio de funcionamiento. Esto hace que si la división cero del nonio coincide con la división cero de la regla, la distancia entre la primera división de la regla y la primera del nonio este desplazada un cuarto de la unidad de la regla; que entre la segunda división de la regla y la segunda del nonio haya una diferencia de dos cuartos de la regla, esto es la mitad de la unidad de la regla; y así, sucesivamente, la cuarta división del nonio coincide con la tercera de la regla, según se ha dicho en la forma de construcción del nonio. Esto hace que en todos los casos en los que el punto 0 del nonio coincida con una división de la regla el último punto del nonio también lo haga.
 |
 |
 |
 |
 |
 |
 |
 |
 |
El fiel indica el número entero de divisiones de la regla, y el nonio o vernier indica su posición entre dos divisiones sucesivas de la regla.
 |
 |
 |
 |
 |
 |
 |
 |
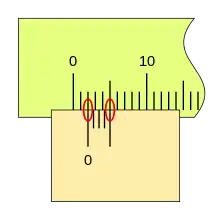 |
Para leer la medida primero se determina la posición del fiel por defecto señala la unidad entera, la división del nonio o vernier indica la parte fraccionaria.
Características del nonio
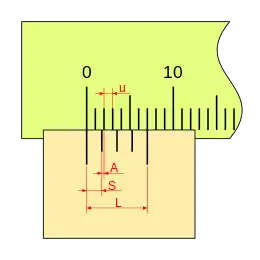
Partiendo de una regla de divisiones igualmente espaciadas se define:
- u: unidad de la regla.
Que, salvo que se especifique otro caso, toma el valor uno en la magnitud que mide la regla.
Una escala nonio se caracteriza por dos valores fundamentales:
- n: número de divisiones del nonio.
- k: constante de extensión.
Donde n y k son números enteros adimensionales, k mayor o igual que 1, normalmente 1 o 2 cuando se quiere facilitar la lectura.
Y podemos ver otras características (derivadas de las anteriores):
- L: longitud del nonio, distancia entre la primera y última división del nonio, medida en la misma unidad de la regla.
- S: separación entre dos divisiones sucesivas del nonio, medida en unidades de la regla.
- A: apreciación, medida más pequeña que puede representar.
Una escala nonio se basa en dos principios fundamentales que la definen (véase figura a la derecha):
1. la longitud del nonio es:
2. la separación entre dos divisiones sucesivas del nonio es:
por lo que tenemos:
de donde obtenemos el valor de la apreciación:A:
cumpliéndose que:
En resumen, para:
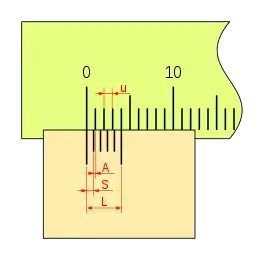
dados, temos que:
y según las relaciones fundamentales, tenemos que:
Influencia de k
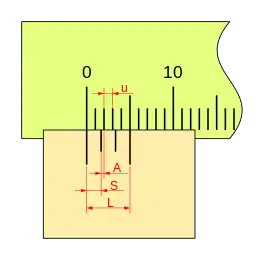
La influencia de los distintos valores de k en un nonio, viene definido por lo siguiente. Definido los valos de k como un número natural:
La separación S, viene determinada por:
para valores sucesivos de k:
Esto es, si para un valor de k la separación de las divisiones del nonio es S, si k se incremente en una unidad, S aumenta en una unidad de la regla: u.
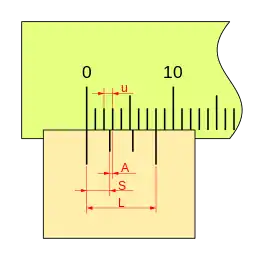
Del mismo modo podemos ver la influencia de k en la longitud total del nonio L, sabiendo que:
Al incrementar k, tenemos:
Si en un nonio de longitud L para un valor de k dado, si se incrementa k en una unidad, la longitud del nonio: L, se incremente en n veces la unidad de la regla u.
La apreciación A, solo depende de la unidad de la regla u, y del número de divisiones del nonio n, el valor de k no influye
La apreciación: A es independiente de la variable de extensión: k.
Las variables del nonio como funciones
El planteamiento, como función, de los distintos valores que definen un nonio, permite ver claramente sus dimensiones y las posibles variantes que admite. Los valores u y n los consideraremos parámetros.
Esto define la apreciación A:
El valor de k está definido por:
Siendo i un número natural, que tomaremos como variable independiente.
La separación entre divisiones del nonio: S está definida:
La longitud del nonio: L será:
La definición de los distintos valores de u y n, que define una apreciación A, para i = 1 definen el nonio más sencillo para esos valores. Si incrementamos progresivamente i el nonio se irá extendiendo en longitud, con la misma apreciación, presentando las distintas opciones posibles, en función de i.
Lectura del nonio
Visto lo anterior, tomando una regla graduada en milímetros, u= 1mm, veamos la lectura de un nonio con un poco más de rigor. Tomaremos como ejemplo uno de cinco divisiones y una constante k = 2.
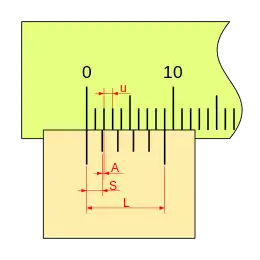
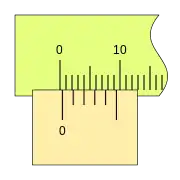
En la figura podemos ver este nonio de cinco divisiones; la línea del fiel esta en la línea cero de la regla, y la última división del nonio coincide con la 9 de la regla.
Si la corredera no dispusiese de una escala nonio, no podríamos apreciar medidas inferiores a las de una división de la regla, como ya se mencionó antes. En este caso las cinco divisiones del nonio nos permiten una apreciación de 0,2mm.
 |
 |
 |
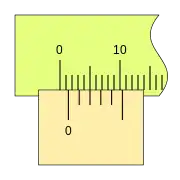 |
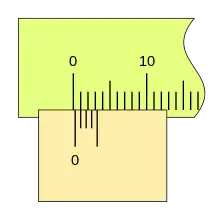
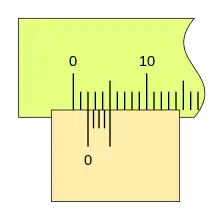
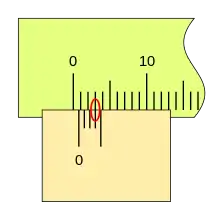
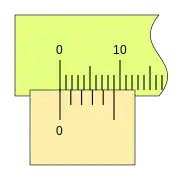
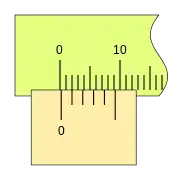
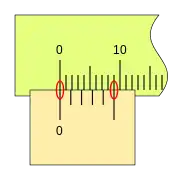
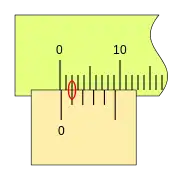
Podemos ver una progresión de medidas de 0,2mm, y la coincidencia sucesiva de las divisiones del nonio con las de la regla.
 |
 |
 |
 |
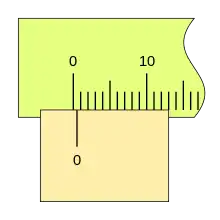
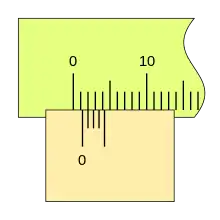
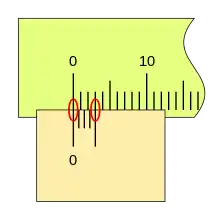
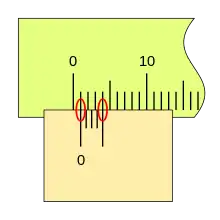
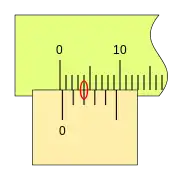
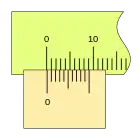
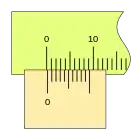
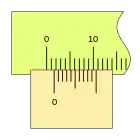
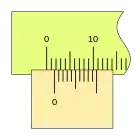
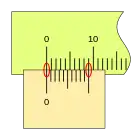
Cuando la lectura es cero (el fiel coincide con el cero de la regla) podemos ver que la última división del nonio también coincide con una división de la regla.
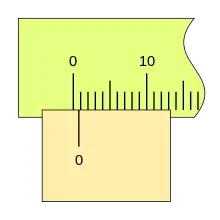
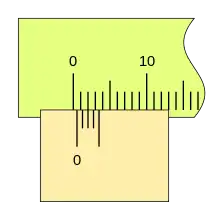
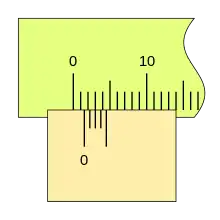
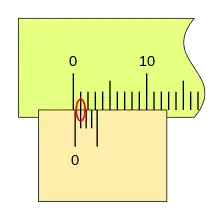
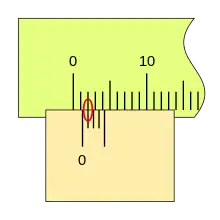
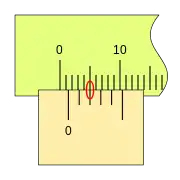
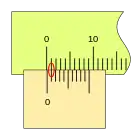
Al desplazarse la corredera, el fiel avanza respecto a la división cero de la regla, si la primera división del nonio coincide con una división de la regla la lectura es 0,2mm.
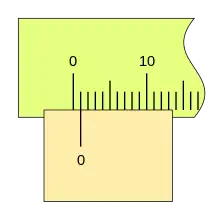
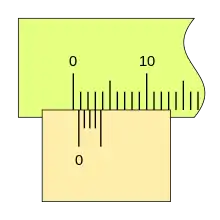
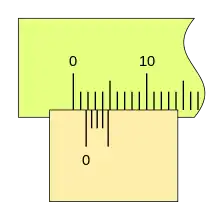
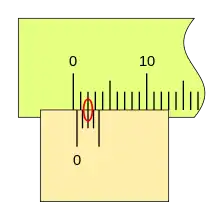
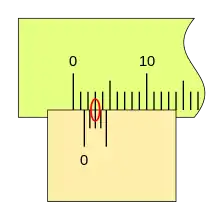
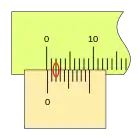
Si la corredera de desplaza más a la derecha y la segunda división de nonio coincide con una división de la regla, la lectura es 0,4mm.
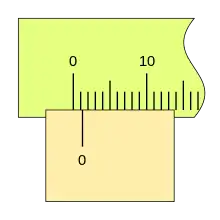
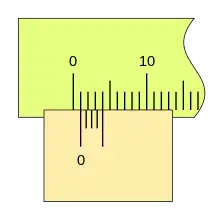
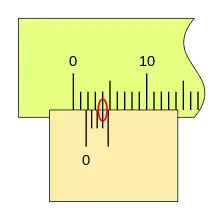
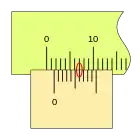
El ciclo se repite, aumentando la medida, cuando la primera división del nonio vuelve a coincidir con una división de la regla (la lectura será 1,0 1,2 1,4 ...), repitiéndose el proceso en toda la longitud de la regla.
La lectura del valor entero en la regla y la parte decimal en el nonio, con la apreciación que corresponda a su número de divisiones, da lugar a poder realizar lecturas de mediciones con mayor precisión que las unidades de la regla. Las distintas formas del nonio o vernier que se pueden construir permiten un abanico de instrumentos adaptable a las distintas necesidades, de una forma ingeniosa, económica y de gran calidad en las medidas.
Nonio de 10 divisiones
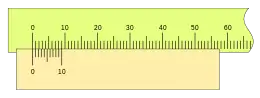
El primer ejemplo visto con anterioridad corresponde a 10 divisiones; con n = 10, tenemos que:
Este nonio, a pesar de su sencillez, es dentro del sistema decimal el más difundido en todo tipo de instrumentos.
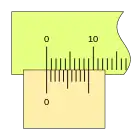 |
 |
 |
 |
 |
 |
 |
 |
 |
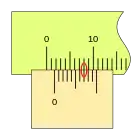 |
Y un buen ejemplo para comprender y adquirir cierta destreza en su manejo, antes de pasar a configuraciones más complejas.
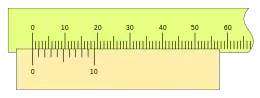
En el caso de que k = 2, tendríamos:
un nonio de 19 mm de longitud y 10 divisiones, tendría la misma apreciación, que uno de 9 mm con 10 divisionas, en el doble de longitud, lo que facilitaría su lectura, al estar sus divisiones más separadas.
 |
 |
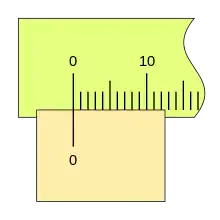
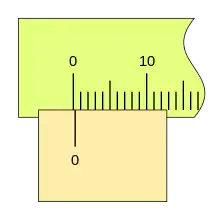
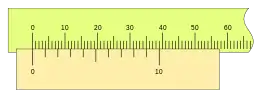
Otro ejemplo de nonio con n= 10 y k= 4 es el de la imagen.
Este caso de nonio en un calibre no es muy usual, siendo su característica más destacada la facilidad de lectura por la gran distancia entre sus divisiones.
En la imagen se ve un calibre con este nonio, cerrado, con lectura 0 mm.
Nonio de 20 divisiones
Podemos ver otro ejemplo, que junto con el anterior, es el más utilizado en el sistema decimal. Un nonio de 19 de longitud y 20 divisiones, con lo que tendríamos:
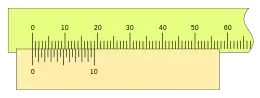
La longitud del nonio de 10 divisiones y k = 2 y 20 divisiones y k = 1 es la misma: 19 mm, como puede verse, pero en este segundo caso las 20 divisiones dan una apreciación de 0,05. En el caso anterior es de 0,1, por la diferencia en el número de divisiones.
Para un calibre Pie de Rey es la mayor apreciación, dado que divisiones más pequeñas no serían apreciables a simple vista, y sería necesario un equipo óptico auxiliar.
Si consideramos la posibilidad con n=20 y k=2, obtendremos una nonio de mayor longitud con la misma apreciación, así:
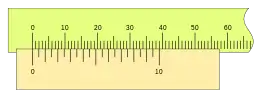 |
 |
En la imagen podemos ver este caso: la apreciación del instrumento es alta, 0,05mm, pero su lectura a simple vista resulta difícil. En la imagen puede verse en 3,50 mm y difícilmente podemos determinar si la lectura es 3,45 mm o 3,55 mm. El límite de la escala nonio viene determinado por la agudeza de la visión del usuario, que no suele superar 0,1 mm con ciertas garantías.
Nonio de 40 divisiones
Un ejemplo muy práctico y poco corriente es el nonio de 40 divisiones y una constante k= 1, con lo que tendríamos:
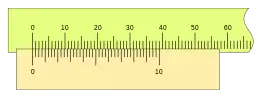
Este nonio tiene una apreciación de 25 micras, cada cuatro divisiones del nonio es una décima de milímetro.
Nonio de 50 divisiones
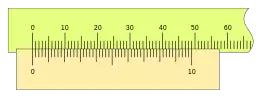
Veamos un nonio de gran apreciación, el de 50 divisiones, sobre una regla en milímetros.
 |
 |
 |
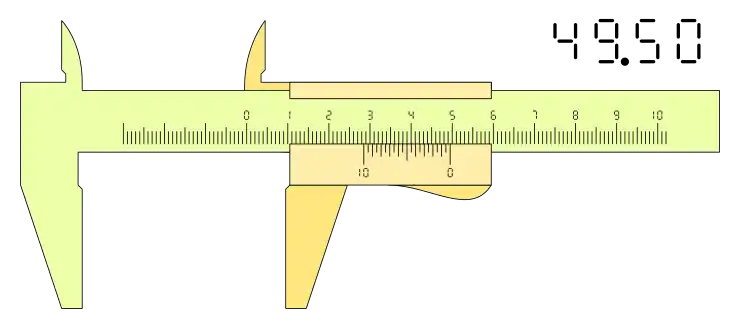
Un nonio de 50 divisiones es el de la fotografía.
La apreciación del instrumento, una división del nonio, equivale a 0,02, cada cinco divisiones son 0,02 * 5 = 0,1. En el nonio o escala vernier, se puede ver que cada cinco divisiones están marcadas con un número: del 0 —que indica el fiel y comienzo de la escala— al 10, indicando las décimas de milímetro.
La segunda fotografía representa en detalle el nonio de la misma imagen, indicando la lectura: 3,58, con dos trazos rojos, uno indica el 3, el valor de la regla anterior al fiel, y la otra la cuarta marca después del 5 en el nonio.
Aun tratándose de una fotografía ampliada, el señalar una lectura con más precisión de 3,6 es difícil. Es fácil percatarse de las dificultades de este calibre para diferenciar medidas de esta precisión, y aunque sí se fabrican y comercializan calibres de este tipo, en la práctica, resultaría poco útil intentar realizar mediciones de más apreciación que 0,05 mm en un calibre a simple vista.
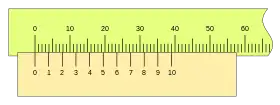
Nonios de igual longitud
 |
 |
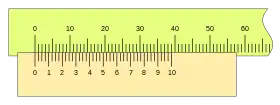 |
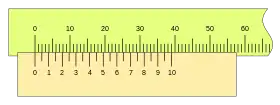
La comparación de distintos nonios de igual longitud nos permite ver la importancia entre las separaciones de las divisiones, por ejemplo con u= 1mm, n=10 y k= 4, tenemos:
con una apreciación A= 0,1mm pero si tomamos los valores: u= 1mm, n=20 y k= 2, tendremos:
con una apreciación A= 0,05mm y con la misma longitud L= 39mm que en el caso anterior, si por el contrario tomamos: u= 1mm, n=40 y k= 1:
con una apreciación A= 0,025mm, viéndose cuatro divisiones entre dos décima de milímetro sucesivas, en una misma longitud del nonio que en los casos anteriores.
Si entre dos divisiones del nonio hay más de una división de la regla, siempre cabe la posibilidad de añadir divisiones al nonio aumentando la apreciación A, y dando lugar, por supuesto, a que las distancia S de separación entre ellas sea menos.
Uso del nonio
El uso del nonio en los instrumentos de medida está muy generalizado, y se emplea en todo tipo de instrumento. Es en el calibre,[20] sin lugar a dudas, donde su utilización es más general y popular. También es utilizado en los planímetros, para cálculo de superficies.
Podemos ver un calibre con nonio o vernier de n= 10 y k= 1:
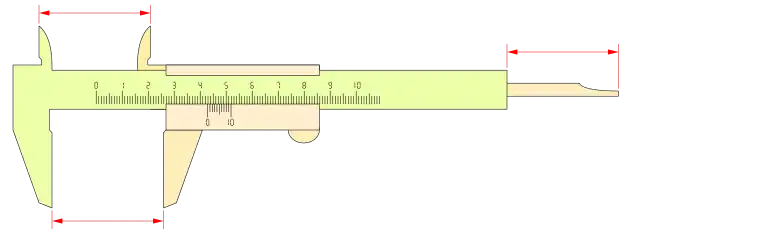
Un mismo calibre puede ser construido con distintos nonios, según las características deseadas. Por ejemplo com n= 10 y k= 2:
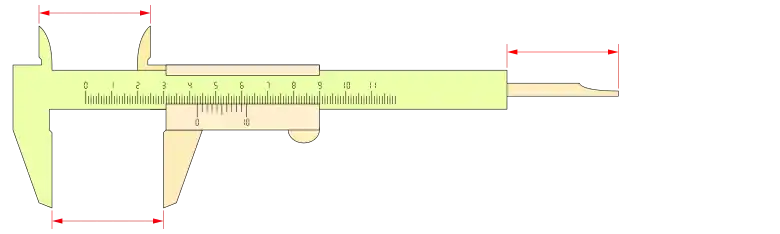
o un nonio o vernier con: n= 20 y k= 1:
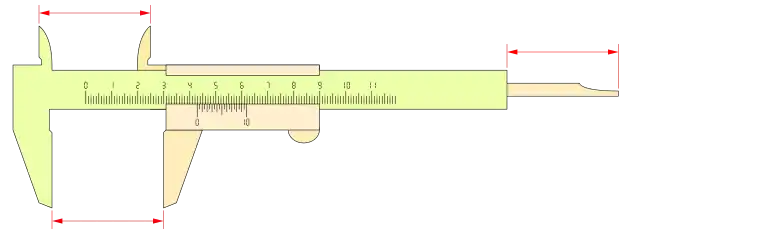
Este instrumento de medida, de gran precisión, que por su bajo coste es versátil y práctico, ha alcanzado una amplia difusión en los más distintos ámbitos.
Nonio en la escala sexagesimal

Hasta ahora hemos visto nonios o escala vernier, en el sistema decimal, donde una unidad inferior es la décima parte, esto es, un dígito a la derecha del anterior. En sistemas no decimales, como por ejemplo el sexagesimal, también se emplea este sistema de medición y la escala del nonio se puede representar en la unidad inferior.
En el sistema sexagesimal, el de medida de ángulos, por ejemplo; en grados, minutos y segundos, donde un grado son sesenta minutos y un minuto sesenta segundos, podemos emplear un nonio del siguiente modo.
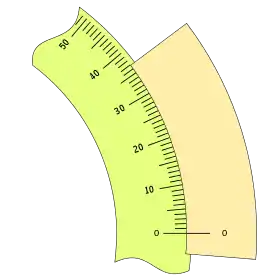
Partiendo de una regla graduada en grados sexagesimal podemos ver que:
y sabemos que:
la apreciación del nonio es:
donde n es el número de divisiones, y la apreciación vendrá dada en grados sexagesimal, por tanto podemos decir:
donde la apreciación vendrá dada en minutos sexagesimal.
Buscando el número n de divisiones entre los divisores de sesenta, tendremos una escala en minutos.
Nonio angular de 12 divisiones
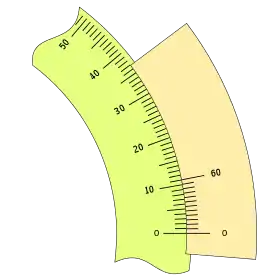
Por ejemplo para n = 12 y k = 1, tendremos:
Según la ordenación de las divisiones puede tomar los siguientes aspectos:
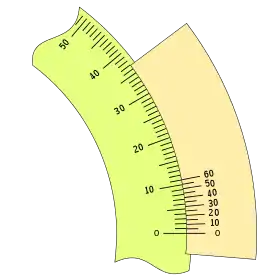 |
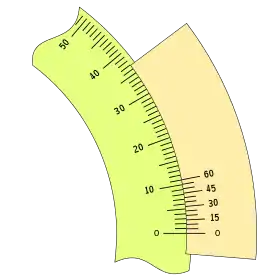 |
Este sencillo Nonio o Vernier, resulta muy práctico con una apreciación de 5 minutos, se pueden agrupar las divisiones es una escala de 10, o en una escala de 15, 30, 45, 60, que en el sistema sexagésimas es muy utilizada.
Nonio angular de 15 divisiones
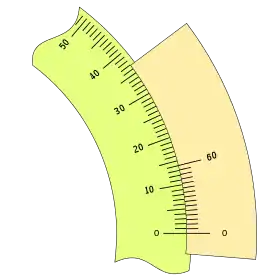
Otro ejemplo sería: n = 15 y k = 1, tendremos:
Diferenciando la forma de numerar las divisiones del nonio, podemos tener dos aspectos diferentes:
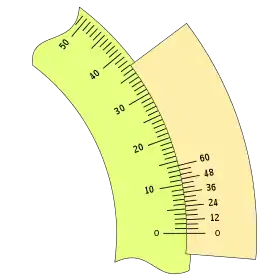 |
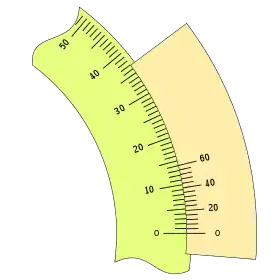 |
Nonio angular de 20 divisiones
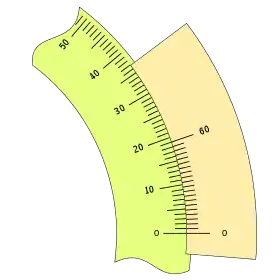
Un caso interesante es: n = 20 y k = 1, tendremos:
Que se puede configurar, destacando algunas de sus divisiones de tres formas:
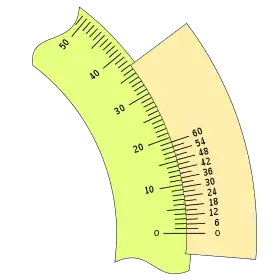 |
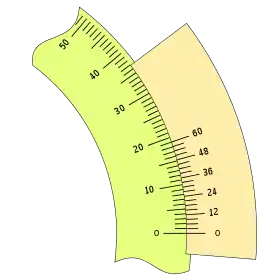 |
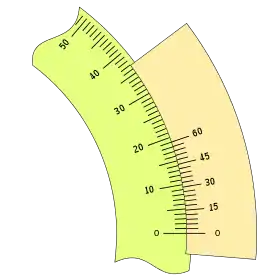 |
Nonio angular de 30 divisiones
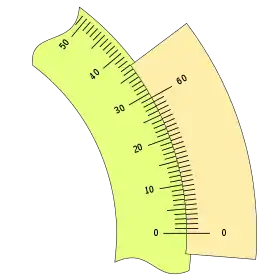
Con los valores: n = 30 y k = 1, tenemos el caso:
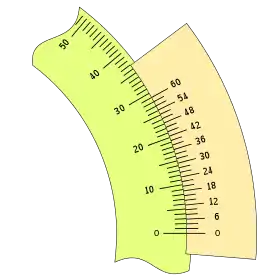
Configurado del siguiente modo:
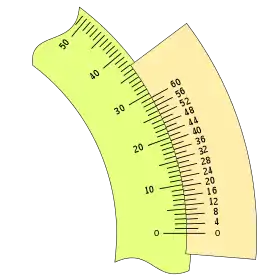 |
 |
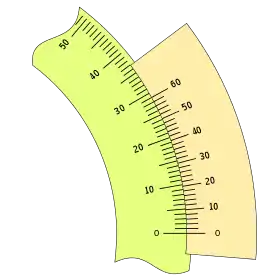 |
El último caso con una apreciación de 2 minutos, señalando las divisiones múltiplos de 10, resulta cómodo de leer en el sistema decimal de numeración.
Longitud del nonio: L = (nk + 1)u. El otro nonio.
Hasta ahora hemos visto L = (nk - 1)u, pero existe otra posibilidad haciendo L = (nk + 1)u.
1. la longitud del nonio:
2. la separación entre dos divisiones sucesivas del nonio:
y tenemos:
y como en el caso anterior tenemos que:
en este caso tenemos:
y según las relaciones fundamentales, tenemos que:
Lectura de este nonio
Como ejemplo tomaremos uno de cinco divisiones y k = 1, comparándolo con el ya analizado.
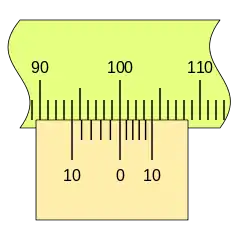
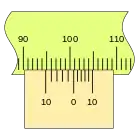
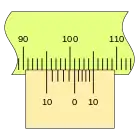
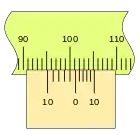
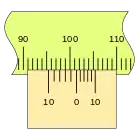
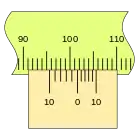
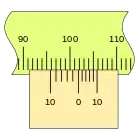
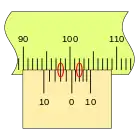
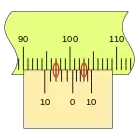
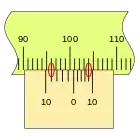
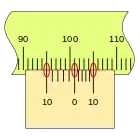
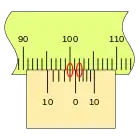
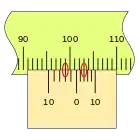
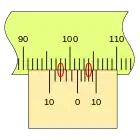
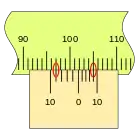
En primer lugar, es apreciable que la separación en este nonio es mayor que en el caso anterior, que las divisiones coinciden en sentido inverso, en el ejemplo sobre la división de la regla 100 mm podemos ver las sucesivas mediciones empleando los dos tipos de nonio.
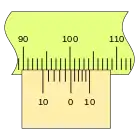 |
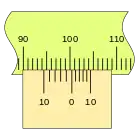 |
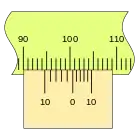 |
 |
 |
 |
 |
 |
 |
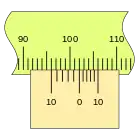 |
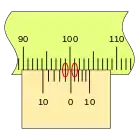
Este nonio se traza desde el punto de medida hacia atrás, por lo que no es lo más indicado para una regla lineal, pero si es muy adecuado para un tambor. por ejemplo.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Nonio de 10 divisiones

En este tipo de nonio, son n y k los parámetros que determinas sus dimensiones, pero a diferencia del primer caso visto, las divisiones se colocan en sentido opuesto al de avance de la corredera.
Las similitudes y las diferencias entre el nonio con: L = (kn - 1)u, y los que tienen L = (kn + 1)u nos permite disponer de una segunda opción para cada caso, definidos por n y k, podemos ver estos dos nonios en una misma regla.
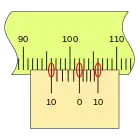
En la figura se puede ver la división del punto de medida, señalada con el número cero, a la derecha del primer nonio con una separaración entre sus divisiones menos que las de la regla, de modo que cuando la corredera se desplaza hacia la derecha irán coincidiendo con una división de la regla sucesivamente.
El segundo nonio se extiende desde el punto de medida hacia la izquierda, la separación de sus divisiones es mayor que las de la regla, de modo que cuando la corredera se desplaza hacia la derecha irán coincidiendo sucesivamente con las divisiones de la regla, del mismo modo que en el primer caso.
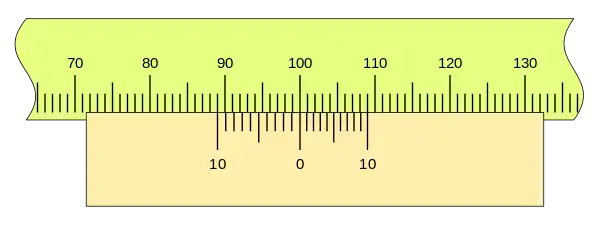
Estas dos opciones de nonio, si bien la primera es la más difundía, debido a que puede ser trazado con una regla que comience desde cero, sin divisiones anteriores, como en un calibre pie de rey. El segundo caso tiene unas divisiones más separada y necesita divisiones en la regla anteriores a la unidad medida, como por ejemplo en un tambor circular.
En el primer caso su división de la izquierda define el punto de medida y el nonio se extiende hacia la derecha, en el segundo caso el punto de medida viene definido por su división derecha si el nonio se extiende hacia la izquierda, esto ha de ser tenido en cuenta sobre todo al utilizar un instrumento de medida que no nos es familiar, nuevo, o de construcción o diseño reciente.
Esta segunda configuración admite el mismo análisis que el primero, y pueden construirse todas las configuraciones para n y k, como en el primer caso. Veamos para n= 10 y k= 2.
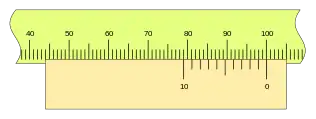
Nonio de 20 divisiones
Un nonio de 20 divisiones, con k= 1, da como resultado una nueva configuración de nonio.
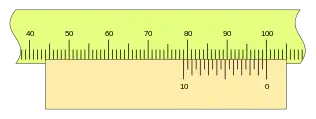
Con lo que tenemos una apreciación de 0,05mm.
Nonio de 40 divisiones
Si tomamos 40 divisiones el resultado es:

En los nonios de n pequeño las diferencias de n+1 y n-1 son muy evidentes, pero a medida que n es mayor la diferencia es más sutil, como es fácil de ver.
Nonio de 50 divisiones
Una configuración de nonio de gran apreciación, casi al límite de la capacidad de apreciación del ojo humano es el de 50 divisiones:
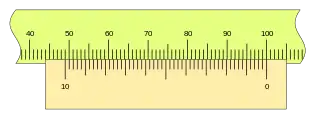
Esta apreciación 0,02mm, dos centésimas de milímetro, efectivamente, es difícil de diferenciar a simple vista, y denota que no simple la construcción de instrumentos de gran apreciación consigue el fin buscado, debido a la agudeza de visión humana, la calidad del instrumento que tiene que garantizar ese grado de calidad, así como el estado de conservación del instrumento, etc.
Nonio n+1 angular
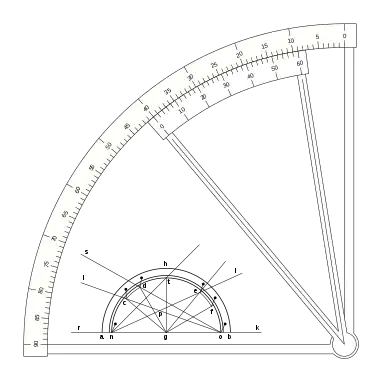
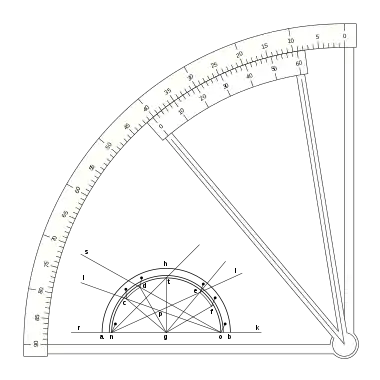
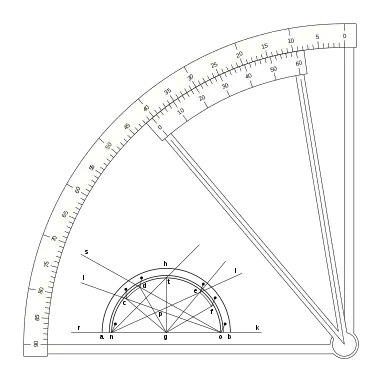
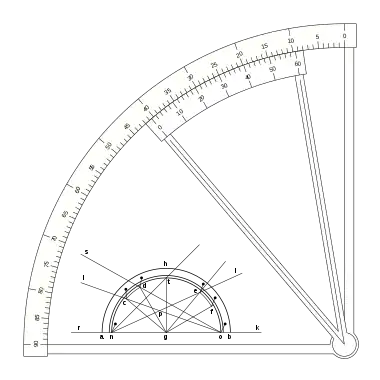
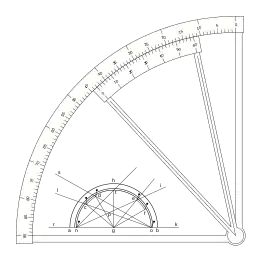
Una escala nonio o vernier que merece un estudio especial es la que presentó Pierre Vernier en su libreo: La Construction, l’usage, et les propriétés du quadrant nouveau de mathématiques ya mencionado. Se trata de una escala de medición angular con una escala en grados sexagesimales, situando el cero en el punto vertical, y una escala nonio o vernier de 30 divisiones que abarca 31 grados de la regla.
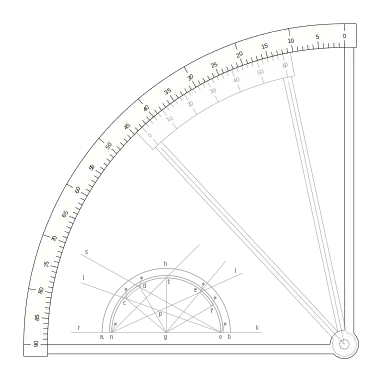 |
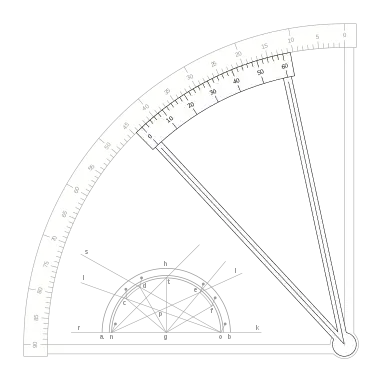 |
Con lo que tenemos:
Puede verse que la escala vernier crece en el sentido decreciente de la regla, la división 0 del vernier indica el punto de medida, y la fracción de grado se puede ver en la división del vernier, que coincide con una división de la regla desde la indicación cero hasta la sesenta, en sentido inverso al sentido creciente de la regla.
Galería de ejemplos
El análisis de un nonio o vernier fuera de contexto puede dar una falsa imagen de la realidad, por lo que podemos ver distintos tipos de nonos o escalas vernier, en un calibre completo, algunas de estas configuraciones son difíciles de ver en calibres reales, pero las mostramos como abanico posible de configuraciones en un calibre.
El ejemplo más clásico tiene diez divisiones con k= 1, en configuración n-1:
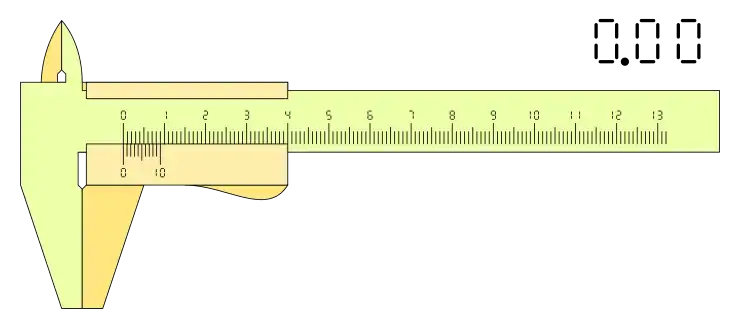
Otra configuración con diez divisiones, k= 1 y configuración: n+1, tenemos:
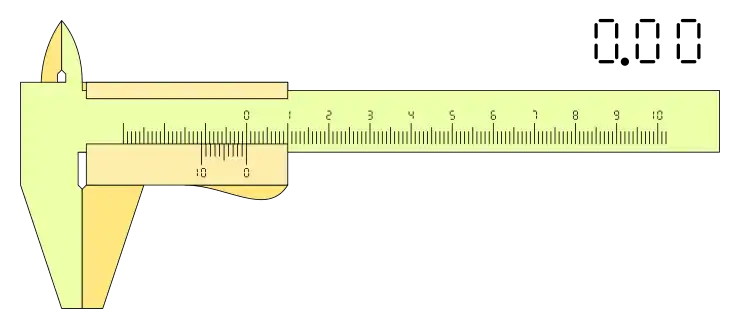
esta cofiguración necesita divisiones de la regla a la izquierda del cero y la lectura de nonio se hace de derecha a izquierda, en contra del caso anterior, esto no redude la horquilla de medidas posibles del calibre, dado que las divisiones adicionales a la izquierda del cero son las mismas divisiones que el nonio n-1 necesita a la derecha en la medida máxima del calibre.
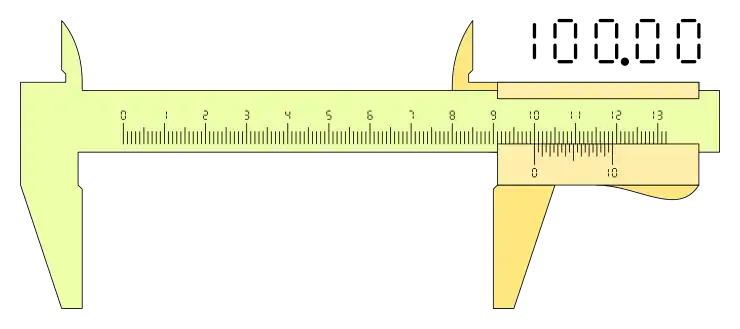
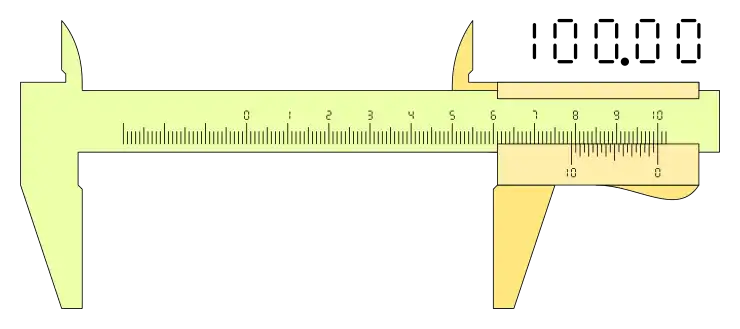
Las diferencias de los distintos calibres que se pueden ver según el nonio o vernier que tenga trazado en la corredera es fundamental para el manejo de este instrumento de medida, podemos ver distintas configuraciones de calibre con distintas medidas:
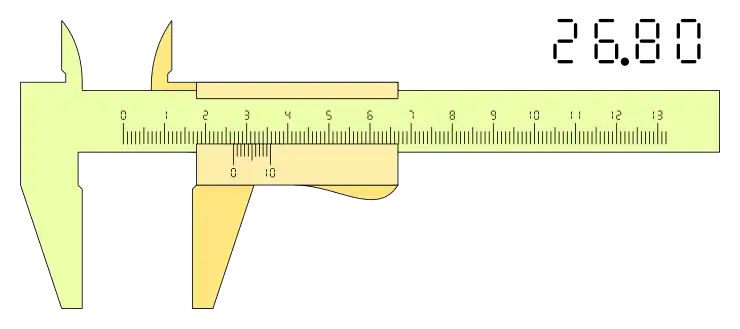
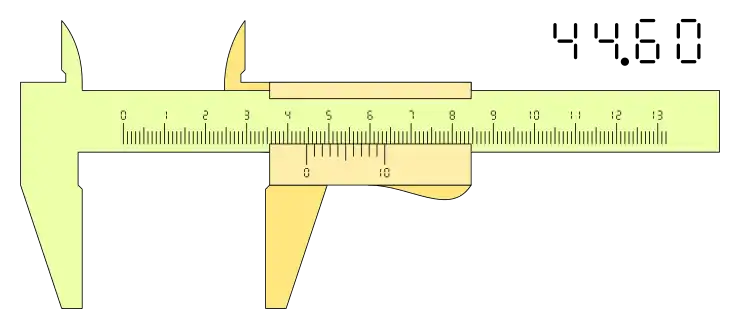
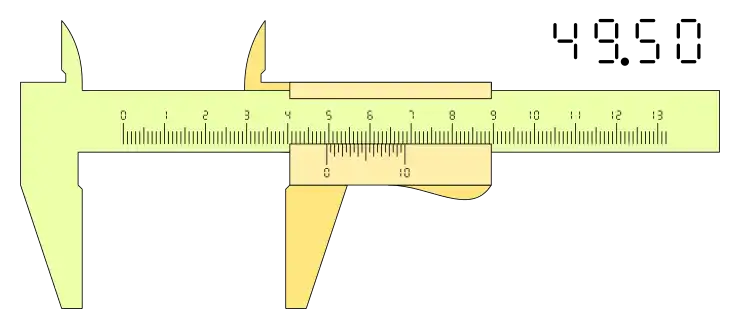
Si la configuración es n+1, el resultado es diferente, téngase en cuenta que en este tipo de nonios la lectura de la medida la determina la división cero de la derecha de nonio y la parte decimal se lee de derecha a izquierda:
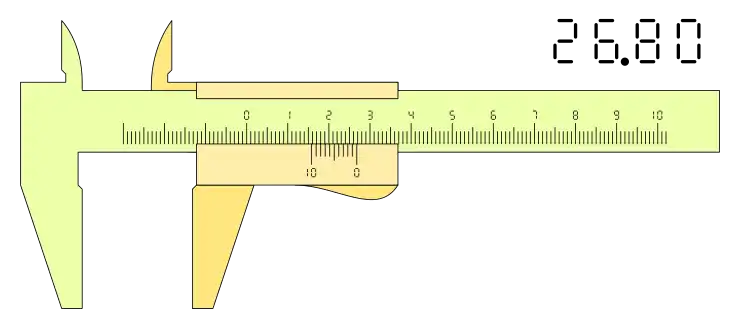
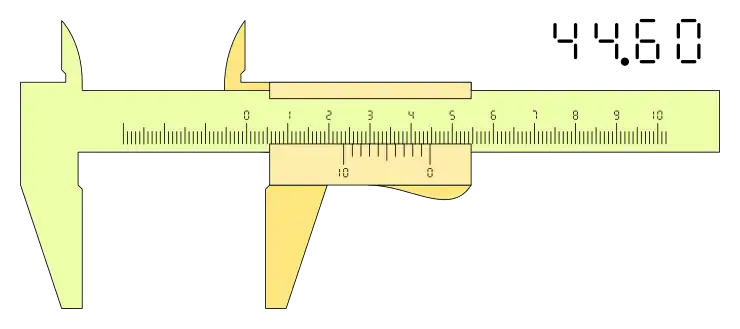
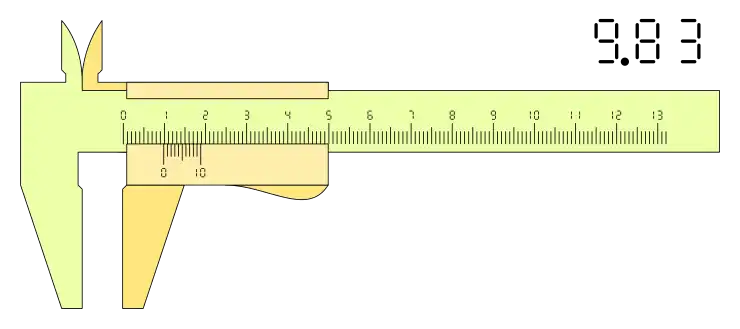
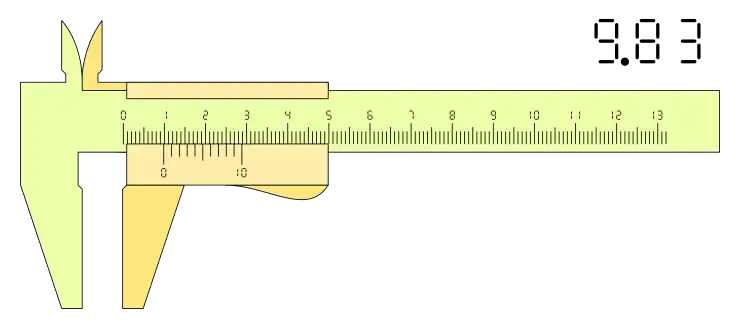
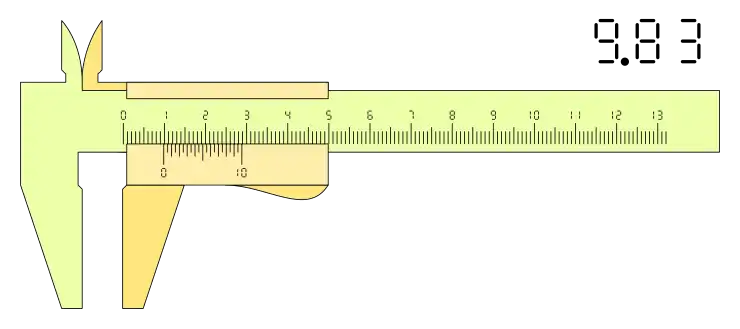
La posición del calibre puede se una cualesquiera dentro de la horquilla de medida, pero la lectura se hace según la apreciación del nonio o Vernier que depende del número de divisiones, por lo tanto, siempre se podrán presentar mediciones que superen esa apreciación, en estos casos se redondea la lectura al velos más próximo según la apreciación del calibre.
Véase también
Referencias
- F. brünnow (1869). «4». Tratado de astronomía esférica (Rafael Pardo de figueroa, trad.) (2 edición). Imprenta de la revista médica. p. 437.
- Ciscar, Gabriel (1851). Tratado de geometria II (6 edición). Imprenta del Ministerio de Comercio. p. 113.
- Dianderas Sánchez, Gerardo (1953). Geografía matemática. Universidad Nacional Mayor de San Marcos. p. 60.
- Frenabdez, Antonio (1994). «3». Manual de Prácticas de Laboratorio. intec. p. 5. ISBN 84-89525-48-X.
- Ginjaume Pujadas, Albert; Torre Crespo, Felipe (2005). «3». Realización de proyectos y piezas en las máquinas herramienta. Paraninfo. p. 38. ISBN 9788497323536.
- «2». Tecnología mecánica 3. Tr. Agustín Cortín. editorial Reverté. 1968. p. 5. ISBN 9788429182217.
- Bernard R. Goldstein (6 de diciembre de 2012). The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Springer Science & Business Media. pp. 164-. ISBN 978-1-4613-8569-1.
- Brian Lasater (2008). The Dream of the West, Pt II. Lulu.com. pp. 355-. ISBN 978-1-4303-1382-3.
- Thomas Digges (1573). Alae seu scalae mathematicae, quibus visibilium remotissima coelorum theatra conscendi, & planetarum omnium itinera nouis & inauditis methodis explorari: ... Thoma Diggeseo, ... authore. pp. 86-.
- Joseph Needham (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 296-. ISBN 978-0-521-05801-8.
- Jean Baptiste Joseph Delambre (1819). Histoire de l'astronomie du moyen age; par m. Delambre, chevalier de Saint-Michel et de la Legion-d'honneur ... mme ve Courcier, imprimeur-libraire pour les sciences. pp. 372-.
- Aimé Laussedat (1898). Recherches sur les instruments: Aperçu historique sur les instruments et les méthodes. La topographie dans tous les temps. Gauthier-Villars.
- Maurice Daumas (1953). Les Instruments scientifiques aux XVIIe et XVIIIe siècles. Presses Universitaires de France.
- A.D. Morrison-Low (2 de marzo de 2017). Making Scientific Instruments in the Industrial Revolution. Taylor & Francis. pp. 61-. ISBN 978-1-351-92074-2.
- António Estácio dos Reis. «Tycho Brahe recorre ao nónio de Pedro Nunes» [Tycho Brahe betakes Pedro Nunes' Nonius]. Ciência Viva. Archivado desde el original el 14 de abril de 2015. Consultado el 7 de noviembre de 2018.
- John Louis Emil Dreyer (13 de febrero de 2014). Tycho Brahe. Cambridge University Press. pp. 58-. ISBN 978-1-108-06871-0.
- Vega Álvarez, José Antonio; López Álvarez, José Luis (2006). «2.2.1». Oficial de Mantenimiento (1 edición). MAD. p. 13. ISBN 978-84-665-5181-6.
- Vernie, Pierre (1631). La Construction, l'usage et les propriétez du quadrant nouveau de mathematique (en francés).
- Vernie, Pierre (2009). La Construction, L'Usage Et Les Proprietez Du Quadrant Nouveau de Mathematique (en francés). Kessinger Publishing.
- Bendix, Friedrich (1978). «1». Alrededor del trabajo de los metales. Editorial Reverte SA. p. 13. ISBN 9788429160307.
Bibliografía
- Esteban José Domínguez; Julián Ferrer (2011). Aparatos y útiles de medida (Mecanizado básico). Editorial: Editex. ISBN 978-84-9003-135-3.
- A. LEYENSETER; G. WÜRTEMBER (2006). Tecnología para oficios metalúrgicos (Carlos Sáenz de Magarola, trad.) (38 edición). Editorial: Reverte S.A. ISBN 978-8429-16-066-6.
- Albert Ginjaume; Felipe Torre (2005). Realización de proyectos y piezas en las máquinas herramienta: libro de prácticas. Editorial Paraninfo.
- Fernando García Márquez (2003). Curso básico de topografía. Editorial Pax México. ISBN 978-968-860-671-1.
- Dietmar Falk; Gockel, H. K.; Lernet, F.; Schlossorsch, B. (1986). Metalotecnia fundamental. Editorial: Reverte S.A. ISBN 978-8429-16-047-5.
Enlaces externos
 Wikimedia Commons alberga una galería multimedia sobre Nonio.
Wikimedia Commons alberga una galería multimedia sobre Nonio. Wikimedia Commons alberga una categoría multimedia sobre Nonio.
Wikimedia Commons alberga una categoría multimedia sobre Nonio. Wikcionario tiene definiciones y otra información sobre nonio.
Wikcionario tiene definiciones y otra información sobre nonio.- La Construction, l'usage et les propriétez du quadrant nouveau de mathematique
- Simulador de prácticas de lectura e interpretación — nonio.
- O Nónio de Pedro Nunes, en Portugués.