Norma del supremo
En análisis matemático, la norma del supremo (o también conocida como la norma uniforme) asigna a funciones acotadas de valores complejos número no negativo
(de una forma análoga podemos definir la norma del supremo para funciones a valores reales ).
Esta norma es también llamada como la norma de Chebyshev, la norma infinito, la norma sup, o también, cuando el supremo es de hecho un máximo, en tal caso pasa a llamarse la norma del máximo. Uno de sus tantos nombres, la "norma uniforme" proviene del hecho de que la sucesión converge a bajo la norma uniforme si y solo si converge a uniformemente.[1]
El matemático Pafnuty Chebyshev fue el primero en estudiar esta norma de manera sistemática (de ahí el nombre de "norma de Chebyshev").
Definición
Sea un conjunto cualquiera, definimos el conjunto de las funciones acotadas en , es decir
,
en otras ocasiones este conjunto suele escribirse como (la letra viene por la palabra bounded en inglés que significa acotada), o también en otros casos o también (se usa este término en casos que la topología de tenga una forma específica). No es difícil ver que mediante las operaciones puntuales el conjunto se transforma en un espacio vectorial.
Si definimos la función de la forma
tenemos que el par se transforma en un espacio vectorial normado, es decir, es una norma. Finalmente a esta función la llamamos como la norma del supremo.
Norma del supremo para funciones no acotadas
Observe que si la condición de ser acotada es retirada, entonces puede existir tal que . Por lo tanto en este caso la función deja de ser una norma, sin embargo es posible definir una topología de todas formas en el espacio y
pasa a ser una métrica extendida.
No es difícil encontrar ejemplos en que . Si consideramos entonces definiendo la función dada por
, para todo
satisface lo que necesitamos.
Ejemplos
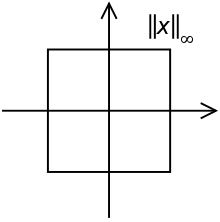
Caso Real y Complejo
Si consideramos al conjunto como un conjunto finito, por ejemplo si , entonces no es difícil notar que (de una manera análoga podemos construir ) y en este caso podemos notar que la norma del supremo toma la forma de la famosa norma del máximo en (o análogamente en ), esto es
.
¿Por qué el subíndice infinito?
Sea la medida de Lebesgue en , entonces definimos la norma p (o también conocida como la p-norma)
,
para toda función tal que sea -medible (observe que este valor puede ser infinito).
Finalmente, si es acotada y existe tal que sea finito entonces se tiene que
- .
Este resultado es generalizable para funciones de tipo donde es un espacio de medida de medida y es una función -medible.
Véase también
Referencias
- Rudin, Walter (1964). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 151. ISBN 0-07-054235-X. (requiere registro).