Oloide
El oloide es un cuerpo geométrico tridimensional creado por Paul Schatz en 1929.[1] Consiste en la envolvente convexa de una estructura construida colocando dos círculos de mismo radio y enlazados en planos perpendiculares, de forma que el centro de cada círculo reside sobre el borde del otro.
Propiedades físicas y aplicaciones
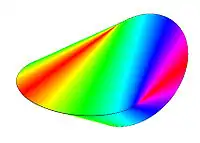
Un oloide se desplaza de una manera suave cuando se lo hace rodar sobre una superficie horizontal plana, debido a que la distancia de su centro de masas a la superficie es prácticamente constante.[2] Esto permite minimizar el trabajo necesario para hacerlo rodar, similar al necesario para rodar una esfera, mientras que permite emplearlo en varias aplicaciones prácticas al crear un tipo especial de turbulencias durante el mismo:
- Se utiliza para el tratamiento y clarificación de aguas ya que sirve para agitar, circular y airear medios líquidos. La técnica produce una corriente orientada, al mismo tiempo que produce impulsos rítmicos por medio del oloide, que da origen a un tipo de agitación muy especial. Esta técnica no daña el medio, produce una alta circulación y utiliza menos energía.[3]
- Sirve como medio de propulsión en navegación.
- Se usa como agitador en biotecnología.
Propiedades y características geométricas


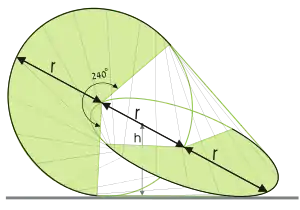
- La distancia entre los centros de los círculos es igual al radio de los mismos.
- Un tercio del perímetro de cada círculo descansa sobre la envolvente convexa, formando parte de la superficie del oloide. Por lo tanto, el mismo oloide se puede definir también como la envolvente convexa de dos arcos de radio r, cada uno de ellos abarcando un ángulo de 4π/3, cuyos centros estén colocados a una distancia r y con orientación perpendicular.
- El área de un oloide construido con círculos de radio r es igual al área de una esfera de radio r .[4]
- El valor numérico del volumen del oloide es
- Para generar un oloide basta con unir mediante segmentos de rectas los pares de puntos A(t) y B(t) cuyas coordenadas vienen dadas por:
Para valores de . El signo positivo en la coordenada z del punto B(t) corresponde a la mitad superior del oloide (por encima del plano xy) y el signo negativo a la mitad inferior.
- La ecuación cartesiana del oloide corresponde a una superficie algebraica de orden 8 cuya expresión viene dada por:[5]
Véase también
Referencias
Enlaces externos
- Construcción de un oloide de madera (inglés)
- Modelo en papel de un oloide
- "Oloid" from The Wolfram Demonstrations Project
- Weisstein, Eric W. «Oloid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Consultado el 27 de mayo de 2010.