Operación interna

Una operación matemática, se dice que es una operación interna, en un conjunto A si para todos los valores de la operación el resultado pertenece a A.[1][2][3][4]

Árbol de clasificación

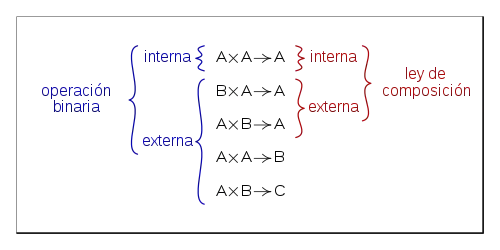
En el caso de un conjunto $A\,$ y una operación binaria $\circledcirc$ definida sobre él $(A,\circledcirc )$ , tendremos que para dos elementos cualesquiera del conjunto A operados bajo $\circledcirc$ , el resultado siempre pertenece al mismo conjunto A. Es decir:

{\displaystyle {\begin{array}{rccl}\circledcirc

El resultado siempre pertenece al mismo conjunto:

\forall a,b\in A:\quad a\circledcirc b\in A

Ejemplo

Sea el conjunto de los números naturales: N y la operación suma: +, $(\mathbb {N} ,+)$ podemos ver:

{\begin{array}{rccl}+:&\mathbb {N} \times \mathbb {N} &\longrightarrow &\mathbb {N} \\&(a,b)&\longmapsto &c=a+b\end{array}}

Se cumple:

\forall x,y\in \mathbb {N

.

Para todo valor x e y que pertenecen a los números naturales, la suma x + y pertenece a los números naturales.

Por lo tanto $(\mathbb {N} ,+)$ es una operación interna.

Si vemos el mismo conjunto de los números naturales y la operación resta: -, $(\mathbb {N} ,-)\,$ tenemos que:

\neg \forall x,y\in N:\quad x-y\in N

.

No para todos los valores x e y que pertenecen a N, x - y pertenece a N, o lo que es lo mismo:

\forall x\in \mathbb {N} ,\quad \exists y\in \mathbb {N

.

Para todo valor x de N, existen valores y de N tal que x - y no pertenece a N, eso se da en todos los casos en los que y es mayor que x, por ejemplo, 3 - 5 no pertenece a N.

La operación resta de los números naturales no es una operación interna.

Véase también

Referencias

Soto Aguilar, Alberto (2011). «1». Elementos de álgebra moderna (1 edición). EUNED. p. 3. ISBN 97-89-9683-1861-7.
del Pozo García, Eva María; Díaz Martínez, Zuleyka; Fernandez Menéndez, José; Segovia Vargas, Mª Jesús (2007). «3». Matemáticas fundamentales para estudios universitarios (1 edición). Delta Publicaciones. p. 8. ISBN 84-933631-6-2.
Díaz Martín, José Fernando; Arsuaga Uriarte, Eider; Riaño Sierra, Jesús M. (2005). «4.1.1». Introducción al álgebra (1 edición). Netbiblo. p. 117. ISBN 84-9745-128-7.
González Carlomán, Antonio (1976). «6.4». Lenguaje matemático: Álgebra I (1 edición). Universidad de Oviedo. p. 426. ISBN 84-400-1624-7.

Bibliografía

Díaz Martín, José Fernando; Arsuaga Uriarte, Eider; Riaño Sierra, Jesús M. (2005). Introducción al Álgebra. Netbiblo. ISBN 84-9745-128-7.
Xambó Descamps, Sebastián Xambó Descamps; Delgado, Félix; Fuertes, Concha (1009). Introducción al álgebra (1 edición). Editorial Complutense. ISBN 9788474914283.

Enlaces externos

Estructuras algebraicas básicas. Universidade da Coruña

Datos: Q15973341

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Soto Aguilar, Alberto (2011). «1». Elementos de álgebra moderna (1 edición). EUNED. p. 3. ISBN 97-89-9683-1861-7.

[2] Pozo García, Eva María; Díaz Martínez, Zuleyka; Fernandez Menéndez, José; Segovia Vargas, Mª Jesús (2007). «3». Matemáticas fundamentales para estudios universitarios (1 edición). Delta Publicaciones. p. 8. ISBN 84-933631-6-2.

[3] Díaz Martín, José Fernando; Arsuaga Uriarte, Eider; Riaño Sierra, Jesús M. (2005). «4.1.1». Introducción al álgebra (1 edición). Netbiblo. p. 117. ISBN 84-9745-128-7.

[4] González Carlomán, Antonio (1976). «6.4». Lenguaje matemático: Álgebra I (1 edición). Universidad de Oviedo. p. 426. ISBN 84-400-1624-7.