Optimización de hiperparámetros
En el aprendizaje automático, la optimización de hiperparámetros [1] o sintonización es el problema de elegir un conjunto de hiperparámetros óptimos para un algoritmo de aprendizaje. Un hiperparámetro es un parámetro cuyo valor se utiliza para controlar el proceso de aprendizaje. En cambio, los valores de otros parámetros (normalmente los pesos de los nodos) se aprenden.
El mismo tipo de modelo de aprendizaje automático puede requerir diferentes restricciones, pesos o ritmos de aprendizaje para generalizar distintos patrones de datos. Estas medidas se denominan hiperparámetros y deben ajustarse para que el modelo pueda resolver de forma óptima el problema de aprendizaje automático. La optimización de hiperparámetros encuentra una tupla de hiperparámetros que produce un modelo óptimo que minimiza una función de pérdida predefinida en datos independientes dados.[2] La función objetivo toma una tupla de hiperparámetros y devuelve la pérdida asociada.[2] La validación cruzada se utiliza a menudo para estimar este rendimiento de generalización, y por lo tanto elegir el conjunto de valores para los hiperparámetros que lo maximizan.[3]
Enfoques
Búsqueda en cuadrícula
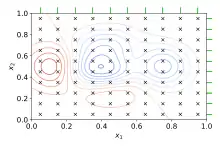
La forma tradicional de realizar la optimización de hiperparámetros ha sido la búsqueda en cuadrícula, o barrido de parámetros, que no es más que una búsqueda exhaustiva a través de un subconjunto especificado manualmente del espacio de hiperparámetros de un algoritmo de aprendizaje. Un algoritmo de búsqueda en cuadrícula debe guiarse por alguna métrica de rendimiento, normalmente medida por validación cruzada en el conjunto de entrenamiento[4] o evaluación en un conjunto de validación de espera.[5]
Dado que el espacio de parámetros de un aprendiz de máquina puede incluir espacios de valores reales o no limitados para ciertos parámetros, puede ser necesario establecer manualmente límites y discretización antes de aplicar la búsqueda de cuadrícula.
Por ejemplo, un clasificador SVM de margen suave típico equipado con un núcleo RBF tiene al menos dos hiperparámetros que deben ajustarse para obtener un buen rendimiento en datos no vistos: una constante de regularización C y un hiperparámetro de núcleo γ. Ambos parámetros son continuos, por lo que para realizar la búsqueda en la cuadrícula, se selecciona un conjunto finito de valores "razonables" para cada uno, digamos:
A continuación, la búsqueda de cuadrícula entrena una SVM con cada par (C, γ) en el producto cartesiano de estos dos conjuntos y evalúa su rendimiento en un conjunto de validación retenido (o mediante validación cruzada interna en el conjunto de entrenamiento, en cuyo caso se entrenan múltiples SVM por par). Por último, el algoritmo de búsqueda en cuadrícula proporciona los ajustes que han obtenido la puntuación más alta en el procedimiento de validación.
La búsqueda de cuadrícula sufre la maldición de la dimensionalidad, pero suele ser vergonzosamente paralela porque los ajustes de hiperparámetros que evalúa suelen ser independientes entre sí.[3]
Búsqueda aleatoria
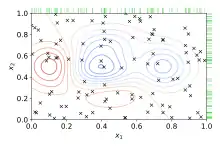
La búsqueda aleatoria sustituye la enumeración exhaustiva de todas las combinaciones por su selección aleatoria. Puede aplicarse de forma sencilla al entorno discreto descrito anteriormente, pero también se generaliza a espacios continuos y mixtos. Puede superar a la búsqueda cuadriculada, especialmente cuando sólo un pequeño número de hiperparámetros afecta al rendimiento final del algoritmo de aprendizaje automático.[3] En este caso, se dice que el problema de optimización tiene una dimensionalidad intrínseca baja.[6] La búsqueda aleatoria también es embarazosamente paralela y, además, permite la inclusión de conocimiento previo especificando la distribución de la que tomar muestras. A pesar de su simplicidad, la búsqueda aleatoria sigue siendo una de las líneas de base importantes con las que comparar el rendimiento de los nuevos métodos de optimización de hiperparámetros.
Optimización bayesiana
Artículo principal: Optimización bayesiana

La optimización bayesiana es un método de optimización global para funciones de caja negra ruidosas. Aplicada a la optimización de hiperparámetros, la optimización bayesiana construye un modelo probabilístico de la función que relaciona los valores de los hiperparámetros con el objetivo evaluado en un conjunto de validación. Mediante la evaluación iterativa de una configuración de hiperparámetros prometedora basada en el modelo actual, y su posterior actualización, la optimización bayesiana pretende recopilar observaciones que revelen tanta información como sea posible sobre esta función y, en particular, sobre la ubicación del óptimo. Intenta equilibrar la exploración (hiperparámetros para los que el resultado es más incierto) y la explotación (hiperparámetros esperados cerca del óptimo). En la práctica, se ha demostrado que la optimización bayesiana[7][8][9][10] obtiene mejores resultados en menos evaluaciones que la búsqueda cuadriculada y la búsqueda aleatoria, debido a la capacidad de razonar sobre la calidad de los experimentos antes de ejecutarlos.
Optimización basada en el gradiente
Para algoritmos de aprendizaje específicos, es posible calcular el gradiente con respecto a los hiperparámetros y, a continuación, optimizar los hiperparámetros mediante el descenso de gradiente. El primer uso de estas técnicas se centró en las redes neuronales.[11] Desde entonces, estos métodos se han extendido a otros modelos como las máquinas de vectores de soporte[12] o la regresión logística.[13]
Un enfoque diferente para obtener un gradiente con respecto a los hiperparámetros consiste en diferenciar los pasos de un algoritmo de optimización iterativo utilizando diferenciación automática.[14][15][16][17] Un trabajo más reciente en esta dirección utiliza el teorema de la función implícita para calcular hipergradientes y propone una aproximación estable del hessiano inverso. El método es escalable a millones de hiperparámetros y requiere memoria constante.
En un enfoque diferente,[18] se entrena una hiperred para aproximar la mejor función de respuesta. Una de las ventajas de este método es que también puede manejar hiperparámetros discretos. Las redes autoajustables[19] ofrecen una versión eficiente en memoria de este enfoque mediante la elección de una representación compacta para la hiperred. Más recientemente, Δ-STN[20] ha mejorado aún más este método mediante una ligera reparametrización de la hiperred que acelera el entrenamiento. Δ-STN también produce una mejor aproximación del jacobiano de mejor respuesta al linealizar la red en los pesos, eliminando así los efectos no lineales innecesarios de los grandes cambios en los pesos.
Además de los enfoques de hiperredes, los métodos basados en gradientes se pueden utilizar para optimizar hiperparámetros discretos también adoptando una relajación continua de los parámetros.[21] Tales métodos se han utilizado ampliamente para la optimización de hiperparámetros de arquitectura en la búsqueda de arquitecturas neuronales.
Optimización evolutiva
Artículo principal: Algoritmo evolutivo
La optimización evolutiva es una metodología para la optimización global de funciones caja negra ruidosas. En la optimización de hiperparámetros, la optimización evolutiva utiliza algoritmos evolutivos para buscar el espacio de hiperparámetros de un algoritmo determinado.[8] La optimización evolutiva de hiperparámetros sigue un proceso inspirado en el concepto biológico de evolución:
- Crear una población inicial de soluciones aleatorias (es decir, generar aleatoriamente tuplas de hiperparámetros, normalmente más de 100).
- Evaluar las tuplas de hiperparámetros y adquirir su función de aptitud (por ejemplo, la precisión de validación cruzada de 10 veces del algoritmo de aprendizaje automático con esos hiperparámetros).
- Clasificar las tuplas de hiperparámetros por su aptitud relativa
- Sustituir las tuplas de hiperparámetros con peor rendimiento por nuevas tuplas de hiperparámetros generadas mediante cruce y mutación.
- Repita los pasos 2-4 hasta que el rendimiento del algoritmo sea satisfactorio o deje de mejorar.
La optimización evolutiva se ha utilizado en la optimización de hiperparámetros para algoritmos de aprendizaje automático estadístico,[8] aprendizaje automático, búsqueda de arquitecturas típicas de redes neuronales[22] y redes neuronales profundas,[23][24] así como en el entrenamiento de los pesos en redes neuronales profundas.[25]
Basado en la población
El entrenamiento basado en la población (PBT) aprende tanto los valores de los hiperparámetros como los pesos de la red. Múltiples procesos de aprendizaje operan de forma independiente, utilizando diferentes hiperparámetros. Al igual que ocurre con los métodos evolutivos, los modelos de bajo rendimiento se sustituyen de forma iterativa por modelos que adoptan valores de hiperparámetros y pesos modificados basados en los de mejor rendimiento. Este arranque en caliente del modelo de sustitución es el principal diferenciador entre PBT y otros métodos evolutivos. PBT permite que los hiperparámetros evolucionen y elimina la necesidad de un ajuste manual. El proceso no hace suposiciones sobre la arquitectura del modelo, las funciones de pérdida o los procedimientos de entrenamiento.
PBT y sus variantes son métodos adaptativos: actualizan los hiperparámetros durante el entrenamiento de los modelos. Por el contrario, los métodos no adaptativos tienen la estrategia subóptima de asignar un conjunto constante de hiperparámetros para todo el entrenamiento.[26]
Parada anticipada
Una clase de algoritmos de optimización de hiperparámetros basados en la parada anticipada está diseñada para grandes espacios de búsqueda de hiperparámetros continuos y discretos, especialmente cuando el coste computacional para evaluar el rendimiento de un conjunto de hiperparámetros es alto. Irace implementa el algoritmo de carrera iterada, que centra la búsqueda en torno a las configuraciones más prometedoras, utilizando pruebas estadísticas para descartar las que rinden mal.[27][28] Otro algoritmo de optimización de hiperparámetros de parada temprana es el de partición sucesiva por la mitad (SHA),[29] que comienza como una búsqueda aleatoria pero periódicamente poda los modelos de bajo rendimiento, centrando así los recursos computacionales en los modelos más prometedores. Las divisiones sucesivas asíncronas (Asynchronous successive halving) (ASHA)[30] mejoran aún más el perfil de utilización de recursos de SHA al eliminar la necesidad de evaluar y eliminar de forma sincrónica los modelos de bajo rendimiento. La hiperbanda[31] es un algoritmo de alto nivel basado en la parada temprana que invoca SHA o ASHA varias veces con distintos niveles de agresividad de poda, para ser más ampliamente aplicable y con menos entradas requeridas.
Otros
También se han desarrollado enfoques de función de base radial (RBF)[32] y métodos espectrales.[33]
Problemas con la optimización de hiperparámetros
Cuando se realiza la optimización de hiperparámetros, el conjunto de hiperparámetros suele ajustarse a un conjunto de entrenamiento y seleccionarse en función del rendimiento de generalización, o puntuación, de un conjunto de validación. Sin embargo, este procedimiento corre el riesgo de sobreajustar los hiperparámetros al conjunto de validación. Por lo tanto, la puntuación del rendimiento de generalización del conjunto de validación (que pueden ser varios conjuntos en el caso de un procedimiento de validación cruzada) no puede utilizarse para estimar simultáneamente el rendimiento de generalización del modelo final. Para ello, el rendimiento de generalización debe evaluarse en un conjunto independiente (que no tenga intersección) del conjunto (o conjuntos) utilizado para la optimización de los hiperparámetros, de lo contrario el rendimiento podría dar un valor demasiado optimista (demasiado grande). Esto puede hacerse en un segundo conjunto de pruebas, o mediante un procedimiento de validación cruzada externa llamado validación cruzada anidada, que permite una estimación insesgada del rendimiento de generalización del modelo, teniendo en cuenta el sesgo debido a la optimización de los hiperparámetros.
Véase también
- Aprendizaje automático
- Búsqueda de arquitectura neuronal
- Metaoptimización
- Selección de modelo
- Autoajuste
- XGBoost
Referencias
- Matthias Feurer and Frank Hutter. «Hyperparameter optimization». AutoML: Methods, Systems, Challenges: 3-38.
- Claesen, Marc; Bart De Moor (2015). Hyperparameter Search in Machine Learning.
- Bergstra, James; Bengio, Yoshua (2012). «Random Search for Hyper-Parameter Optimization». Journal of Machine Learning Research: 281-305.
- Chin-Wei Hsu, Chih-Chung Chang and Chih-Jen Lin (2010). «A practical guide to support vector classification». Technical Report, National Taiwan University.
- Chicco, Davide (8 de diciembre de 2017). «Ten quick tips for machine learning in computational biology». BioData Mining 10: 35. ISSN 1756-0381. PMC 5721660. PMID 29234465. doi:10.1186/s13040-017-0155-3. Consultado el 17 de septiembre de 2023.
- Ziyu, Wang; Frank, Hutter; Masrour, Zoghi; David, Matheson; Nando, de Feitas (2016). «Bayesian Optimization in a Billion Dimensions via Random Embeddings». Journal of Artificial Intelligence Research: 361-387. doi:10.1613/jair.4806.
- Hutter, Frank; Hoos, Holger; Leyton-Brown, Kevin (2011). «Sequential model-based optimization for general algorithm configuration». Learning and Intelligent Optimization, Lecture Notes in Computer Science: 507-523. ISBN 978-3-642-25565-6. doi:10.1007/978-3-642-25566-3_40.
- Bergstra, James; Bardenet, Remi; Bengio, Yoshua; Kegl, Balazs (2011). «Algorithms for hyper-parameter optimization». Advances in Neural Information Processing Systems.
- Snoek, Jasper; Larochelle, Hugo; Adams, Ryan (2012). «Practical Bayesian Optimization of Machine Learning Algorithms». Advances in Neural Information Processing Systems.
- Thornton, Chris; Hutter, Frank; Hoos, Holger; Leyton-Brown, Kevin (2013). «Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms». Knowledge Discovery and Data Mining.
- Larsen, Jan; Hansen, Lars Kai; Svarer, Claus; Ohlsson, M (1996). «Design and regularization of neural networks: The optimal use of a validation set». Neural Networks for Signal Processing VI. Proceedings of the 1996 IEEE Signal Processing Society Workshop: 62-71. ISBN 0-7803-3550-3. doi:10.1109/NNSP.1996.548336.
- «The Geeks Zone». thegeekszone.com (en inglés estadounidense). Consultado el 18 de septiembre de 2023.
- Chuong B; Chuan-Sheng Foo; Andrew Y Ng (2008). «Efficient multiple hyperparameter learning for log-linear models». Advances in Neural Information Processing Systems.
- Domke, Justin (2012). «Generic Methods for Optimization-Based Modeling». Aistats.
- Maclaurin, Douglas; Duvenaud, David; Adams, Ryan P. (2015). Gradient-based Hyperparameter Optimization through Reversible Learning.
- Franceschi, Luca; Donini, Michele; Frasconi, Paolo; Pontil, Massimiliano (2017). «Forward and Reverse Gradient-Based Hyperparameter Optimization». Proceedings of the 34th International Conference on Machine Learning.
- Shaban, A., Cheng, C. A., Hatch, N., & Boots, B. (2019). «Truncated back-propagation for bilevel optimization». The 22nd International Conference on Artificial Intelligence and Statistics: 1723-1732.
- Lorraine, J., & Duvenaud, D. (2018). Stochastic hyperparameter optimization through hypernetworks.
- MacKay, M., Vicol, P., Lorraine, J., Duvenaud, D., & Grosse, R. (2019). Self-tuning networks: Bilevel optimization of hyperparameters using structured best-response functions.
- Bae, J., & Grosse, R. B. (2020). «Delta-stn: Efficient bilevel optimization for neural networks using structured response jacobians». Advances in Neural Information Processing Systems.
- Liu, H., Simonyan, K., & Yang, Y. (2018). Darts: Differentiable architecture search..
- Kousiouris, George; Cucinotta, Tommaso; Varvarigou, Theodora (1 de agosto de 2011). «The effects of scheduling, workload type and consolidation scenarios on virtual machine performance and their prediction through optimized artificial neural networks». Journal of Systems and Software 84 (8): 1270-1291. ISSN 0164-1212. doi:10.1016/j.jss.2011.04.013. Consultado el 18 de septiembre de 2023.
- Jaderberg M, Dalibard V, Osindero S, Czarnecki WM, Donahue J, Razavi A, Vinyals O, Green T, Dunning I, Simonyan K, Fernando C, Kavukcuoglu K (2017). Population Based Training of Neural Networks.
- Such FP, Madhavan V, Conti E, Lehman J, Stanley KO, Clune J (2017). Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning.
- Li, Ang; Spyra, Ola; Perel, Sagi; Dalibard, Valentin; Jaderberg, Max; Gu, Chenjie; Budden, David; Harley, Tim; Gupta, Pramod (2019). A Generalized Framework for Population Based Training.
- López-Ibáñez, Manuel; Dubois-Lacoste, Jérémie; Pérez Cáceres, Leslie; Birattari, Mauro; Stützle, Thomas (1 de enero de 2016). «The irace package: Iterated racing for automatic algorithm configuration». Operations Research Perspectives 3: 43-58. ISSN 2214-7160. doi:10.1016/j.orp.2016.09.002. Consultado el 18 de septiembre de 2023.
- Birattari, Mauro; Stützle, Thomas; Paquete, Luis; Varrentrapp, Klaus (2022). «A Racing Algorithm for Configuring Metaheuristics». Gecco 2002.
- Jamieson, Kevin; Talwalkar, Ameet (2015). Non-stochastic Best Arm Identification and Hyperparameter Optimization.
- Li, Liam; Jamieson, Kevin; Rostamizadeh, Afshin; Gonina, Ekaterina; Hardt, Moritz; Recht, Benjamin; Talwalkar, Ameet (2020). A System for Massively Parallel Hyperparameter Tuning.
- Li, Lisha; Jamieson, Kevin; DeSalvo, Giulia; Rostamizadeh, Afshin; Talwalkar, Ameet (2020). «Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization». Journal of Machine Learning Research.
- Diaz, Gonzalo; Fokoue, Achille; Nannicini, Giacomo; Samulowitz, Horst (2017). An effective algorithm for hyperparameter optimization of neural networks.
- Hazan, Elad; Klivans, Adam; Yuan, Yang (2017). Hyperparameter Optimization: A Spectral Approach.