Proceso de ortogonalización de Gram-Schmidt

En álgebra lineal, el proceso de ortogonalización de Gram–Schmidt es un algoritmo para construir, a partir de un conjunto de vectores de un espacio vectorial con producto interno, otro conjunto ortonormal de vectores que genere el mismo subespacio vectorial.

Animación que describe el proceso de ortonormalización en el espacio tridimensional.

El proceso se basa en un resultado de la geometría euclídea, el cual establece que la diferencia entre un vector $\mathbf {v}$ y su proyección sobre otro vector $\mathbf {u}$ , es perpendicular al vector $\mathbf {u}$ .[1] Dicho resultado constituye una herramienta para construir, a partir de un conjunto de dos vectores no paralelos, otro conjunto, conformado por dos vectores perpendiculares.

Este algoritmo recibe su nombre de los matemáticos Jørgen Pedersen Gram y Erhard Schmidt.

Interpretación geométrica

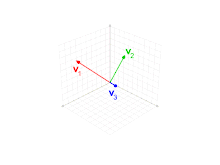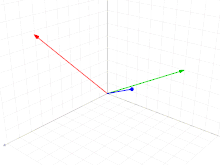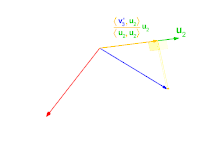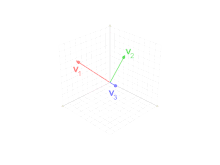
En el espacio euclídeo $\mathbb {R} ^{3}$ con el producto escalar usual definido, se propone un método para encontrar un sistema de vectores, perpendiculares entre sí, a partir de tres vectores no coplanarios cualesquiera. Sean $\mathbf {v} _{1},\mathbf {v} _{2},\mathbf {v} _{3}\in \mathbb {R} ^{3}$ dichos vectores.

El método consiste de dos proyecciones. La base ortogonal de $\mathbb {R} ^{3}$ compuesta por $\mathbf {u} _{1},\mathbf {u} _{2},\mathbf {u} _{3}$ , se calcula de la siguiente manera.

Se escoge arbitrariamente uno de los vectores dados, por ejemplo, $\mathbf {u} _{1}=\mathbf {v} _{1}$ .
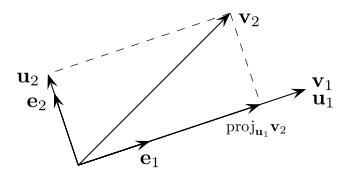
$\mathbf {u} _{2}$ se calcula como la diferencia entre $\mathbf {v} _{2}$ y el vector que resulta de proyectar a $\mathbf {v} _{2}$ sobre $\mathbf {u} _{1}$ . Dicha diferencia es perpendicular a $\mathbf {u} _{1}$ . Es equivalente afirmar que $\mathbf {u} _{2}$ es la diferencia entre $\mathbf {v} _{2}$ y el vector que resulta de proyectar a $\mathbf {v} _{2}$ sobre la recta que genera $\mathbf {u} _{1}$ .
$\mathbf {u} _{3}$ es la diferencia entre $\mathbf {v} _{3}$ y el vector que resulta de proyectar a $\mathbf {v} _{3}$ sobre el plano generado por $\mathbf {u} _{1}$ y $\mathbf {u} _{2}$ . La diferencia de vectores tiene como resultado otro vector que es perpendicular al plano.

Esta sencilla interpretación del algoritmo para un caso que puede verse es susceptible de generalización a espacios vectoriales de dimensión arbitraria, con productos internos definidos, no necesariamente canónicos. Dicha generalización no es otra que el proceso de Gram-Schmidt.

Descripción del algoritmo de ortogonalización de Gram–Schmidt

Los dos primeros pasos del proceso de Gram–Schmidt

El método de Gram-Schmidt se usa para hallar bases ortogonales (Espacio Euclideo no normalizado) de cualquier base no euclídea.

En primer lugar tenemos que:

\mathbf {v} -{\langle \mathbf {v} ,\mathbf {u} \rangle  \over \langle \mathbf {u} ,\mathbf {u} \rangle }\mathbf {u} =\mathbf {v} -\mathrm {proy} _{\mathbf {u} }\,(\mathbf {v} )

Es un vector ortogonal a $\mathbf {u}$ . Entonces, dados los vectores $\mathbf {v} _{1},\dots ,\mathbf {v} _{n}$ , se define:

	$\mathbf {u} _{1}=\mathbf {v} _{1},$
	$\mathbf {u} _{2}=\mathbf {v} _{2}-{\langle \mathbf {v} _{2},\mathbf {u} _{1}\rangle \over \langle \mathbf {u} _{1},\mathbf {u} _{1}\rangle }\mathbf {u} _{1},$
	$\mathbf {u} _{3}=\mathbf {v} _{3}-{\langle \mathbf {v} _{3},\mathbf {u} _{1}\rangle \over \langle \mathbf {u} _{1},\mathbf {u} _{1}\rangle }\mathbf {u} _{1}-{\langle \mathbf {v} _{3},\mathbf {u} _{2}\rangle \over \langle \mathbf {u} _{2},\mathbf {u} _{2}\rangle }\mathbf {u} _{2},$ Generalizando en k:
	$\mathbf {u} _{k}=\mathbf {v} _{k}-\sum _{j=1}^{k-1}{\langle \mathbf {v} _{k},\mathbf {u} _{j}\rangle \over \langle \mathbf {u} _{j},\mathbf {u} _{j}\rangle }\mathbf {u} _{j}$

A partir de las propiedades del producto escalar, es sencillo probar que el conjunto de vectores $\mathbf {u} _{1},\dots ,\mathbf {u} _{n}$ es ortogonal.

Proposición 1

Si

${\mathcal {B}}=\left\{\mathbf {v} _{1},\mathbf {v} _{2},\dots ,\mathbf {v} _{k}\right\}$

es un conjunto de vectores linealmente independientes, los vectores u₁, u₂, ... u_k definidos por

$\left\{{\begin{array}{rcll}\mathbf {u} _{1}&=&\mathbf {v} _{1}&\\\mathbf {u} _{k}&=&\mathbf {v} _{k}-\displaystyle \sum _{j=1}^{k-1}\operatorname {proy} _{\mathbf {u} _{j}}\left(\mathbf {v} _{k}\right)&{\textrm {para}}\ k>1\end{array}}\right.$

son todos no nulos. Dicho de otra manera, para cada k,

$\left\langle u_{k},u_{k}\right\rangle \neq 0.$

Demostración
Procedemos por inducción. Supongamos que fuese $\mathbf {u} _{1}=\mathbf {0}$ esto implica por definición de u₁ que $\mathbf {v} _{1}=\mathbf {0}$ lo cual contradice la hipótesis de que ${\mathcal {B}}$ es linealmente independiente. Luego, $\mathbf {u} _{1}\neq \mathbf {0} .$ Establezcamos la hipótesis inductiva como sigue. $\forall j<k,\ \mathbf {u} _{j}\neq \mathbf {0}$ Expresamos v₁, v₂, ... v_k en función de los u₁, u₂, ... u_k de la siguiente manera. ${\begin{bmatrix}1&0&\cdots &0\\{\frac {\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\{\frac {\left\langle \mathbf {u} _{1},\mathbf {v} _{k}\right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}&{\frac {\left\langle \mathbf {u} _{2},\mathbf {v} _{k}\right\rangle }{\left\langle \mathbf {u} _{2},\mathbf {u} _{2}\right\rangle }}&\cdots &1\end{bmatrix}}{\begin{bmatrix}\mathbf {u} _{1}&\mathbf {u} _{2}&\cdots &\mathbf {u} _{k}\end{bmatrix}}={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{k}\end{bmatrix}}$ En la expresión, se ve que es posible despejar u_k en función de una sucesión v_j de vectores, puesto que la matriz del conjunto de sistemas es triangular inferior, con todos sus elementos en la diagonal distintos de cero. Esto implica en particular que existen escalares $\mu _{(2)(1)},\dots ,\mu _{(k)(1)},\dots \mu _{(k)(2)},\dots \mu _{(k)(k-1)}$ (tantos como elementos en el triángulo inferior de la matriz inversa) tales que $\mathbf {u} _{k}=\mathbf {v} _{k}+\sum _{j=1}^{k-1}\mu _{(k)(j)}\mathbf {v} _{j}.$ Supongamos que fuera u_k = 0, en este caso queda $0=\mathbf {v} _{k}+\sum _{j=1}^{k-1}\mu _{(k)(j)}\mathbf {v} _{j}$ y por lo tanto existen escalares, no todos nulos, que producen una combinación nula con vectores de ${\mathcal {B}}$ . Esto contradice la hipótesis de que ${\mathcal {B}}$ es linealmente independiente. Luego, $\mathbf {u} _{k}\neq \mathbf {0}$ igualdad que, por el principio de inducción, es válida para todo k natural∎

Proposición 2

El conjunto

${\mathcal {E}}=\left\{\mathbf {u} _{1},\mathbf {u} _{2},\dots ,\mathbf {u} _{k}\right\}$

está constituido por vectores mutuamente ortogonales.

Demostración
Sea $P=\left\{(n,k)\in \mathbb {N} \times \mathbb {N$ Debemos aplicar dos veces el principio de inducción para probar que $P=\mathbb {N} \times \mathbb {N} .$ Comencemos por probar que $\forall k\in \mathbb {N} ,\,(1,k)\in P.$ De la Proposición 1 se deduce que $\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle \neq 0$ lo cual por un lado, implica que (1, 1) está en P, y por otro, permite definir el vector (1) $\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v_{2}} \right)=\left({\frac {\left\langle \mathbf {u} _{1},\mathbf {v_{2}} \right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}\right)\mathbf {u} _{1}$ Por la linealidad del producto interno, se tiene $\left\langle \mathbf {u} _{1},\mathbf {u} _{2}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{2}-\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle -\left\langle \mathbf {u} _{1},\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)\right\rangle$ que, en (1), queda $\left\langle \mathbf {u} _{1},\mathbf {u} _{2}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle -\left\langle \mathbf {u} _{1},\left({\frac {\left\langle \mathbf {u} _{1},\mathbf {v_{2}} \right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}\right)\mathbf {u} _{1}\right\rangle$ finalmente, por la homogeneidad del producto interno tenemos $\left\langle \mathbf {u} _{1},\mathbf {u} _{2}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle -\left({\frac {\left\langle \mathbf {u} _{1},\mathbf {v_{2}} \right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}\right)\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle -\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle =0$ luego $(1,2)\in P.$ Procedemos por inducción, la hipótesis inductiva es $\forall j,\ 1<j<k\Longrightarrow \left\langle \mathbf {u} _{1},\mathbf {u} _{j}\right\rangle =0.$ La Proposición 1, permite definir $\operatorname {proy} _{\mathbf {u} _{j}}\left(\mathbf {v} _{k}\right)=\left({\frac {\left\langle \mathbf {u} _{j},\mathbf {v_{k}} \right\rangle }{\left\langle \mathbf {u} _{j},\mathbf {u} _{j}\right\rangle }}\right)\mathbf {u} _{j}$ con lo cual, análogamente al caso j = 2, se tiene $\left\langle \mathbf {u} _{1},\mathbf {u} _{k}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{k}\right\rangle -\sum _{j=1}^{k-1}\left({\frac {\left\langle \mathbf {u} _{j},\mathbf {v_{k}} \right\rangle }{\left\langle \mathbf {u} _{j},\mathbf {u} _{j}\right\rangle }}\right)\left\langle \mathbf {u} _{1},\mathbf {u} _{j}\right\rangle =\left\langle \mathbf {u} _{1},\mathbf {v} _{k}\right\rangle -\left\langle \mathbf {u} _{1},\mathbf {v_{k}} \right\rangle =0.$ Esto demuestra que $\forall k\in \mathbb {N} ,\,(1,k)\in P$ es decir, todo vector en ${\mathcal {E}}$ es perpendicular a u₁, con excepción del mismo u₁. Aplicaremos inducción sobre n, considérese la hipótesis inductiva $\forall j<n,(j,k)\in P$ también puede escribirse $\forall j<n,\forall k\in \mathbb {N} ,\left(j<k\Longrightarrow \left\langle \mathbf {u} _{j},\mathbf {u} _{k}\right\rangle =0\land \left\langle \mathbf {u} _{j},\mathbf {u} _{j}\right\rangle \neq 0\right)$ La Proposición 1 garantiza la segunda condición de la conjunción lógica, con lo cual sólo hace falta demostrar para n la primera. $\left\langle \mathbf {u} _{n},\mathbf {u} _{k}\right\rangle =\left\langle \mathbf {u} _{n},\mathbf {v} _{k}\right\rangle -\sum _{j=1}^{k-1}\left({\frac {\left\langle \mathbf {u} _{j},\mathbf {v_{k}} \right\rangle }{\left\langle \mathbf {u} _{j},\mathbf {u} _{j}\right\rangle }}\right)\left\langle \mathbf {u} _{n},\mathbf {u} _{j}\right\rangle =\left\langle \mathbf {u} _{n},\mathbf {v} _{k}\right\rangle -\left\langle \mathbf {u} _{n},\mathbf {v_{k}} \right\rangle =0.$ por lo tanto $P=\mathbb {N} \times \mathbb {N} \quad \blacksquare$

Los conjuntos así definidos satisfacen la siguiente relación.

Proposición 3

Los sistemas de vectores

${\mathcal {B}}=\left\{\mathbf {v} _{1},\mathbf {v} _{2},\dots \mathbf {v} _{k}\right\},\,{\mathcal {E}}=\left\{\mathbf {u} _{1},\mathbf {u} _{2},\dots \mathbf {u} _{k}\right\}$

generan el mismo subespacio vectorial.

Para obtener una base ortonormal a partir de ${\mathcal {E}}$ , basta con dividir entre la norma de cada vector de la base hallada: $\mathbf {e} _{k}={\mathbf {u} _{k} \over ||\mathbf {u} _{k}||}={\mathbf {u} _{k} \over {\sqrt {\langle \mathbf {u} _{k},\mathbf {u} _{k}\rangle }}}$

Ejemplos

Dada ${\mathcal {B}}=\left\{\mathbf {v} _{1},\mathbf {v} _{2}\right\}$ una base de $\mathbb {R} ^{2}$ definida por

$\left\{{\begin{array}{rcl}\mathbf {v} _{1}&=&{\begin{bmatrix}2\\1\end{bmatrix}}\\\mathbf {v} _{2}&=&{\begin{bmatrix}1\\4\end{bmatrix}}\end{array}}\right.$

mediante el proceso de Gram-Schmidt es posible construir una base ortogonal ${\mathcal {E}}=\left\{\mathbf {u} _{1},\mathbf {u} _{2}\right\}$ con respecto al producto interno usual de $\mathbb {R} ^{2}$ .

$\left\langle (a,b),(c,d)\right\rangle =ac+bd$ .

Se calculan los vectores u₁ y u₂ a partir de las fórmulas.

$\left\{{\begin{array}{rlcl}\mathbf {u} _{1}=&\mathbf {v} _{1}&=&{\begin{bmatrix}2\\1\end{bmatrix}}\\&\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)&=&{\frac {\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}\mathbf {u} _{1}={\begin{bmatrix}{\frac {12}{5}}\\{\frac {6}{5}}\end{bmatrix}}\\\mathbf {u} _{2}=&\mathbf {v} _{2}-\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)&=&{\begin{bmatrix}-{\frac {7}{5}}\\{\frac {14}{5}}\end{bmatrix}}\end{array}}\right.$

nótese que

${\begin{bmatrix}-{\frac {7}{5}}\\{\frac {14}{5}}\end{bmatrix}}={\frac {7}{5}}{\begin{bmatrix}-1\\2\end{bmatrix}}$

de hecho, dado cualquier vector $(a,b)\in \mathbb {R} ^{2}$ y $\forall \;\alpha \in \mathbb {R}$ se cumple

$\left\langle (a,b),\alpha (-b,a)\right\rangle =0$ .
Sea ${\mathcal {B}}=\left\{\mathbf {v} _{1},\mathbf {v} _{2},\mathbf {v} _{3}\right\}$ el sistema definido por

$\left\{{\begin{array}{rcl}\mathbf {v} _{1}&=&{\begin{bmatrix}2\\1\\1\end{bmatrix}}\\\mathbf {v} _{2}&=&{\begin{bmatrix}1\\0\\10\end{bmatrix}}\\\mathbf {v} _{3}&=&{\begin{bmatrix}2\\-3\\11\end{bmatrix}}\end{array}}\right.$

Aplicamos el proceso, seleccionamos por ejemplo

$\mathbf {u} _{1}=\mathbf {v} _{1}={\begin{bmatrix}2\\1\\1\end{bmatrix}}$

y calculamos

$\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)={\frac {\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle }{\left\langle \mathbf {u} _{1},\mathbf {u} _{1}\right\rangle }}\mathbf {u} _{1}={\begin{bmatrix}4\\2\\2\end{bmatrix}}$

luego

$\mathbf {u} _{2}=\mathbf {v} _{2}-\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{2}\right)={\begin{bmatrix}-3\\-2\\8\end{bmatrix}}$ .

Análogamente se sigue para u₃ que

$\left\{{\begin{array}{rcc}\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{3}\right)&=&{\begin{bmatrix}4\\2\\2\end{bmatrix}}\\\operatorname {proy} _{\mathbf {u} _{2}}\left(\mathbf {v} _{3}\right)&=&{\begin{bmatrix}-{\frac {24}{7}}\\-{\frac {16}{7}}\\{\frac {64}{7}}\end{bmatrix}}\\\mathbf {u} _{3}=\mathbf {v} _{3}-\operatorname {proy} _{\mathbf {u} _{1}}\left(\mathbf {v} _{3}\right)-\operatorname {proy} _{\mathbf {u} _{2}}\left(\mathbf {v} _{3}\right)&=&{\begin{bmatrix}{\frac {10}{7}}\\-{\frac {19}{7}}\\-{\frac {1}{7}}\end{bmatrix}}\end{array}}\right.$

finalmente se obtiene

${\mathcal {E}}=\left\{\mathbf {u} _{1},\mathbf {u} _{2},\mathbf {u} _{3}\right\}=\left\{{\begin{bmatrix}2\\1\\1\end{bmatrix}},{\begin{bmatrix}-3\\-2\\8\end{bmatrix}},{\begin{bmatrix}{\frac {10}{7}}\\-{\frac {19}{7}}\\-{\frac {1}{7}}\end{bmatrix}}\right\}$

que es una base ortogonal de R³ con respecto al producto escalar canónico.

Descripción formal

Una manera de expresar el algoritmo explícitamente es a través de pseudocódigo. Se construye, para ello, una función con las siguientes características.

Tiene como entrada un conjunto ${\mathcal {B}}$ no vacío de vectores linealmente independientes.
Recibe dos instrucciones iterativas anidadas.
1. Una estructura para cada, que asigna a v un vector de la entrada, por cada iteración.
2. Una estructura mientras, que asigna a u el vector ortogonal a todos los u calculados en las iteraciones previas.
En cada iteración, se ejecutan las funciones
1. Proy, la cual calcula la proyección ortogonal de un vector sobre otro. Se define matemáticamente como sigue.
  $\operatorname {Proy} :V\times V\longrightarrow V,\,\operatorname {Proy} \left(v_{1},v_{2}\right)=\left({\frac {\left\langle v_{1},v_{2}\right\rangle }{\left\|v_{2}\right\|^{2}}}\right)v_{2}$ donde V es un espacio vectorial.
2. obtener, como su nombre lo indica, obtiene el elemento de un conjunto dado su ordinal.
Devuelve finalmente un conjunto ${\mathcal {E}}$ de vectores ortogonales.

Algoritmo Gram-Schmidt
función $\operatorname {ortogonalizar} ({\mathcal {B}})$ ${\mathcal {E}}\gets \emptyset ,\,i\gets 0$ para $\mathbf {v} \,$ en ${\mathcal {B}}\,$ haga $\mathbf {u} \gets \mathbf {v} ,\,j\gets 0$ mientras $i>j$ $\mathbf {u} \gets \mathbf {u} -\operatorname {Proy} \left(\mathbf {v} ,\operatorname {obtener} ({\mathcal {E}},j)\right),\,j\gets j+1$ agregue $\mathbf {u} \,$ a ${\mathcal {E}}$ $i\gets i+1$ devuelva ${\mathcal {E}}$

Para obtener una base ortonormal, basta normalizar los elementos de ${\mathcal {E}}$ .

Proceso de ortogonalización de Gram-Schmidt con el método de Gauss

Dada una matriz M cuyos vectores fila son los vectores de una base a ortogonalizar, si se aplica la eliminación Gaussiana por filas a la matriz $(M\cdot M^{t}|M)$ .

Ejemplo

Se realiza con la eliminación de Gauss la ortogonalización de Gram-Schmidt a la base dada por las filas de $M$ :

2	1	1
1	0	10
2	-3	11

Para ello escribimos a la derecha la matriz de su producto escalar $M\cdot M^{t}$

6	12	12	2	1	1
12	101	112	1	0	10
12	112	134	2	-3	11

Y se realiza la eliminación Gaussiana

A Fila2 le restamos la Fila1 por 2

A Fila3 le restamos la Fila1 por 2

6	12	12	2	1	1
0	77	88	-3	-2	8
0	88	110	-2	-5	9

A Fila3 por 7 le restamos la Fila2 por 8

6	12	12	2	1	1
0	77	88	-3	-2	8
0	0	66	10	-19	-1

Las filas de la derecha son una base ortogonal,

*	*	*	2	1	1
*	*	*	-3	-2	8
*	*	*	10	-19	-1

cuyos vectores son proporcionales a los que se obtuvieron anteriormente con el proceso de Gram-Schmidt.

Referencias

Sullivan, Michael. Trigonometría y geometría analítica (4ª edición). México: Pearson educación. p. 403. ISBN 9789688809433.

Datos: Q475239

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Sullivan, Michael. Trigonometría y geometría analítica (4ª edición). México: Pearson educación. p. 403. ISBN 9789688809433.