Pantalón (matemáticas)
En matemáticas, un pantalón es una superficie que es homeomórfica a una esfera con tres orificios. El nombre proviene de considerar uno de los discos eliminados como la cintura y los otros dos como las bocas de las perneras de un pantalón.
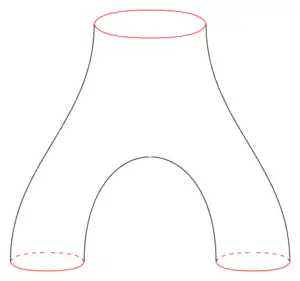
Los pantalones se utilizan como bloques de construcción para las superficies compactas en varias teorías. Dos aplicaciones importantes son para la geometría hiperbólica, donde se utilizan descomposiciones de superficies mediante pantalones para construir sistemas de coordenadas de Fenchel-Nielsen en el espacio de Teichmüller, y en teoría topológica cuántica de campo, donde son los cobordismos no triviales más simples entre las variedades unidimensionales.
Pantalones y su descomposición
Pantalones como superficies topológicas
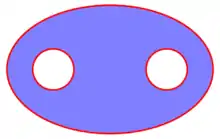
Matemáticamente, un pantalón es cualquier superficie homeomorfa a una esfera con tres orificios, que formalmente es el resultado de quitar de la esfera tres discos con cierres disjuntos por pares. Así, un pantalón es una superficie compacta de genus cero con tres fronteras.
La característica de Euler de un par de pantalones es igual a −1, y la única otra superficie con esta propiedad es el toro perforado (un toro menos una abertura en forma de disco).
Descomposiciones de un pantalón
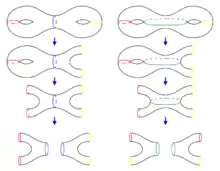
La importancia de los pantalones en el estudio de las superficies se deriva de la siguiente propiedad: definir la complejidad de una superficie compacta conexa de genus con componentes de contorno como , y para una superficie no conexa tomar la suma de todos los componentes. Entonces, las únicas superficies con característica de Euler negativa y complejidad cero son uniones disjuntas de pantalones. Además, para cualquier superficie y cualquier curva simple cerrada sobre que no sea homotópica para un componente límite, la superficie compacta obtenida cortando en tiene una complejidad estrictamente menor que . En este sentido, los pantalones son las únicas superficies "irreducibles" entre todas las superficies de característica negativa de Euler.
Por un argumento recursivo, esto implica que para cualquier superficie existe un sistema de curvas cerradas simples que cortan la superficie en pantalones. Esto se denomina "descomposición en pantalones" de la superficie, y las curvas obtenidas se denominan "puños" de la descomposición. Esta descomposición no es única, pero al cuantificar el argumento se ve que todas las descomposiciones en pantalones de una superficie dada tienen el mismo número de curvas, que es exactamente su complejidad.[1] Para superficies conexas, una descomposición en pantalones tiene exactamente pantalones.
Una colección de curvas cerradas simples sobre una superficie es una descomposición en pantalones si y solo si son inconexas, dos de ellas no son homotópicas y ninguna es homotópica a un componente de contorno, y la colección es máxima para estas propiedades.
Complejo de pantalones
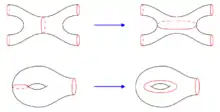
Una superficie dada tiene infinitas descomposiciones en pantalones distintas (se entiende que dos descomposiciones son distintas cuando no son homotópicas). Una forma de tratar de entender las relaciones entre todas estas descomposiciones es el complejo de pantalones asociado a la superficie. Este es un grafo con vértice establecido en las descomposiciones en pantalones de , y dos vértices se unen si están relacionados por un movimiento elemental, que es una de las dos operaciones siguientes:
- Tómese una curva en la descomposición en un toro de un agujero y reemplácese por una curva en el toro que lo interseca solo una vez,
- Tómese una curva en la descomposición en una esfera de cuatro orificios y reemplácese por una curva en la esfera que la interseca solo dos veces.
El complejo de pantalones es conexo[2] (lo que significa que dos descomposiciones de pantalones están relacionadas por una secuencia de movimientos elementales) y tiene diámetro infinito (lo que significa que no hay un límite superior en el número de movimientos necesarios para pasar de una descomposición a la otra). En el caso particular cuando la superficie tiene complejidad 1, el complejo de pantalones es isomórfico a la sucesión de Farey.
La acción del grupo de clase de aplicación en el complejo de los pantalones es de interés para el estudio de este grupo. Por ejemplo, Allen Hatcher y William Thurston lo han usado para demostrar que es de presentación finita.
Pantalones en geometría hiperbólica
Módulo del espacio de pantalón hiperbólico
Las interesantes estructuras hiperbólicas de un pantalón se clasifican fácilmente.[3]
- Para todo existe una superficie hiperbólica que es homeomorfa a un pantalón y cuyas componentes de contorno son geodésicas cerradas simples de longitudes iguales a . Tal superficie está determinada únicamente por salvo isometrías.
Al tomar la longitud de un puño (boca de pernera) igual a cero, se obtiene una mátrica completa en el pantalón menos el puño, que se reemplaza por un cúspide. Esta estructura es de volumen finito.
Pantalones y hexágonos
La prueba geométrica de la clasificación en el párrafo anterior es importante para comprender la estructura de un pantalón hiperbólico. Se procede de la siguiente manera: Dado un pantalón hiperbólico con límite totalmente geodésico, existen tres arcos geodésicos únicos que unen los puños por pares y que son perpendiculares a ellos en sus extremos. Estos arcos se llaman las "costuras" de los pantalones.
Al cortar un pantalón por sus costuras, se obtienen dos hexágonos hiperbólicos en ángulo recto que tienen tres lados alternos de longitudes a juego. El siguiente lema se puede probar con geometría hiperbólica elemental.[4]
- Si dos hexágonos hiperbólicos en ángulo recto tienen cada uno tres lados alternos de longitudes iguales, entonces son isométricos entre sí.
Entonces se comprueba que el pantalón es el doble de un hexágono en ángulo recto en lados alternos. Dado que la clase de isometría del hexágono también está determinada únicamente por las longitudes de los tres lados alternos restantes, la clasificación del pantalón se deriva de la de los hexágonos.
Cuando la longitud de un puño es cero, se reemplaza el lado correspondiente en el hexágono en ángulo recto por un vértice ideal.
Coordenadas de Fenchel-Nielsen
Un punto en el espacio de Teichmüller de una superficie está representado por un par , donde es una superficie hiperbólica completa y un difeomorfismo.
Si tiene una descomposición en pantalones por las curvas , entonces se pueden parametrizar los pares de Teichmüller mediante las coordenadas de Fenchel-Nielsen, que se definen a continuación. Las "longitudes de puño" son simplemente las longitudes de las geodésicas cerradas homotópicas a .
Los "parámetros de torsión" son más difíciles de definir. Corresponden a cuánto se gira al pegar dos pantalones en : esto se define define por el módulo . Se puede refinar la definición (utilizando la continuación analítica [5] o técnicas geométricas) para obtener parámetros de giro valorados en (más o menos, el punto es que cuando se hace un giro completo, cambia el punto en el espacio de Teichmüller al precomponer con un giro de Dehn alrededor de ).
El complejo de los pantalones y la métrica de Weil-Petersson
Se puede definir una aplicación del complejo de pantalones al espacio de Teichmüller, que lleva una descomposición de pantalones a un punto elegido arbitrariamente en la región donde la parte del puño de las coordenadas de Fenchel-Nielsen está limitada por una constante lo suficientemente grande. Es una quasi-isometría cuando el espacio de Teichmüller está dotado de la métrica de Weil-Petersson, que ha demostrado su utilidad en el estudio de esta métrica.[6]
Pantalón y grupos de Schottky
Estas estructuras corresponden a grupos de Schottky en dos generadores (más precisamente, si el cociente de la geometría hiperbólica por un grupo de Schottky en dos generadores es homeomorfo al interior de un pantalón, entonces su núcleo convexo es un pantalón hiperbólico como se describe arriba, y todos se obtienen como tales).
Cobordismos bidimensionales
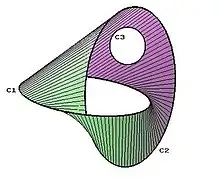
Un cobordismo entre dos variedades cerradas n-dimensionales es una variedad compacta (n+1)-dimensional cuyo límite es la unión disjunta de las dos variedades. La categoría de cobordismos de dimensión n+1 es la categoría con objetos de las variedades cerradas de dimensión n, y son morfismos los cobordismos entre ellos (nótese que la definición de un cobordismo incluye la identificación del límite de las variedades). Téngase en cuenta que una de las variedades puede estar vacía; en particular, una variedad cerrada de dimensión n+1 se ve como un endomorfismo del conjunto vacío. También se pueden componer dos cobordismos cuando el final del primero es igual al inicio del segundo. Una teoría cuántica topológica de campo n-dimensional (TQFT) es un funtor monoide de la categoría de "n"-cobordismos a la categoría de espacio vectorial complejo (donde la multiplicación viene dada por el producto tensorial).
En particular, los cobordismos entre variedades unidimensionales (que son uniones de círculos) son superficies compactas cuyo límite se ha separado en dos uniones disjuntas de circunferencias. Los TQFT bidimensionales corresponden a un álgebra de Frobenius, donde el círculo (la única 1-variedad cerrada conexa) se asigna al espacio vectorial subyacente del álgebra, mientras que el pantalón da un producto o coproducto, dependiendo de cómo se agrupen los componentes del límite: que es conmutativo o coconmutativo. Además, la aplicación asociada con un disco da una counidad (traza) o unidad (escalares), dependiendo de la agrupación del límite, que completa la correspondencia.
Referencias
- Ratcliffe, 2006, Theorem 9.7.1.
- Hatcher y Thurston, 1980.
- Ratcliffe, 2006, Theorem 9.7.3.
- Ratcliffe, 2006, Theorem 3.5.14.
- Imayoshi y Taniguchi, 1992, p. 63.
- Brock, Jeff (2002). «Pants decompositions and the Weil-Petersson metric». En Earle, Clifford J.; Harvey, William J.; Recillas-Pishmish, Sevín, eds. Complex Manifolds and Hyperbolic Geometry. Contemporary Mathematics 311. Providence, RI: American Mathematical Society. pp. 27-40. ISBN 978-0-8218-7901-6. doi:10.1090/conm/311/05445.
Bibliografía
- Hatcher, Allen; Thurston, William (1980). «A presentation for the mapping class group of a closed orientable surface». Topology 19 (3): 221-237. doi:10.1016/0040-9383(80)90009-9.
- Imayoshi, Yôichi; Taniguchi, Masahiko (1992). An introduction to Teichmüller spaces. Springer. pp. xiv+279. ISBN 4-431-70088-9.
- Ratcliffe, John (2006). Foundations of hyperbolic manifolds, Second edition. Springer. pp. xii+779. ISBN 978-0387-33197-3.