Perceptrón multicapa
El perceptrón multicapa es una red neuronal artificial (RNA) formada por múltiples capas, de tal manera que tiene capacidad para resolver problemas que no son linealmente separables, lo cual es la principal limitación del perceptrón (también llamado perceptrón simple). El perceptrón multicapa puede estar totalmente o localmente conectado. En el primer caso cada salida de una neurona de la capa "i" es entrada de todas las neuronas de la capa "i+1", mientras que en el segundo cada neurona de la capa "i" es entrada de una serie de neuronas (región) de la capa "i+1".
Tipos
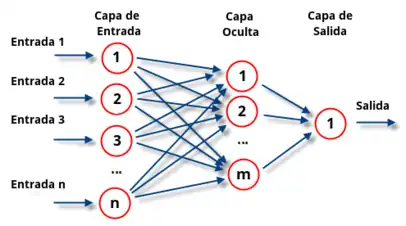
Las capas pueden clasificarse en tres tipos:
- Capa de entrada: Constituida por aquellas neuronas que introducen los patrones de entrada en la red. En estas neuronas no se produce procesamiento.
- Capas ocultas: Formada por aquellas neuronas cuyas entradas provienen de capas anteriores y cuyas salidas pasan a neuronas de capas posteriores.
- Capa de salida: Neuronas cuyos valores de salida se corresponden con las salidas de toda la red.
La propagación hacia atrás (también conocido como retropropagación del error o regla delta generalizada), es un algoritmo utilizado en el entrenamiento de estas redes, por ello, el perceptrón multicapa también es conocido como red de retropropagación (no confundir con la red de contrapropagación).
Historia
En 1969, Minsky y Papert, demuestran que el perceptrón simple y ADALINE no puede resolver problemas no lineales (por ejemplo, XOR). La combinación de varios perceptrones simples podría resolver ciertos problemas no lineales pero no existía un mecanismo automático para adaptar los pesos de la capa oculta. Rumelhart y otros autores, en 1986, presentan la "Regla Delta Generalizada" para adaptar los pesos propagando los errores hacia atrás, es decir, propagar los errores hacia las capas ocultas inferiores. De esta forma se consigue trabajar con múltiples capas y con funciones de activación no lineales. Se demuestra que el perceptrón multicapa es un aproximador universal. Un perceptrón multicapa puede aproximar relaciones no lineales entre los datos de entrada y salida. Esta red se ha convertido en una de las arquitecturas más utilizadas en el momento.[1]
Características
- Las funciones de transferencia de los elementos de procesado (neuronas) han de ser derivables.
Limitaciones
- El Perceptrón Multicapa no extrapola bien, es decir, si la red se entrena mal o de manera insuficiente, las salidas pueden ser imprecisas.
- La existencia de mínimos locales en la función de error dificulta considerablemente el entrenamiento, pues una vez alcanzado un mínimo el entrenamiento se detiene aunque no se haya alcanzado la tasa de convergencia fijada.
Cuando caemos en un mínimo local sin satisfacer el porcentaje de error permitido se puede considerar: cambiar la topología de la red (número de capas y número de neuronas), comenzar el entrenamiento con unos pesos iniciales diferentes, modificar los parámetros de aprendizaje, modificar el conjunto de entrenamiento o presentar los patrones en otro orden.
Aplicaciones
El perceptrón multicapa (de aquí en adelante MLP, MultiLayer Perceptron) se utiliza para resolver problemas de asociación de patrones, segmentación de imágenes, compresión de datos, etc.
Aprendizaje a través de la retropropagación
El aprendizaje ocurre en el perceptrón cambiando los pesos de las conexiones después de cada elemento se procese, basado en la cantidad del error en la salida comparada con el resultado esperado. Esto es un ejemplo de aprendizaje supervisado y se lleva a cabo a través de la retropropagación, una generalización del algoritmo LMS (menor media cuadrática) en el perceptrón lineal.
Representamos el error en el nodo en el punto de datos como , donde es el valor objetivo y es el valor producido por el perceptrón. Cuando hacemos las correcciones a los pesos de los nodos basados en estas correcciones las cuales minimizan el error en toda la salida, dado por
- .
Usando un descenso de gradiente, encontramos que nuestro cambio en cada peso es
Donde es la salida de la neurona anterior y es el ritmo de aprendizaje, que se selecciona cuidadosamente para que los pesos converjan a una respuesta lo suficientemente rápido, sin producir oscilaciones. En la programación de aplicaciones este parámetro generalmente va de 0.2 a 0.8
La derivada a ser calculada depende del campo local inducido , el cual varía por sí mismo. Es fácil probar que para un nodo de salida esta derivada puede ser simplificada a
Donde es la derivada de la función de activación descrita más arriba, la cual no varía. El análisis es más complicada para el cambio en pesos en un nodo oculto, pero puede mostrarse que la derivada relevante es
- .
Esto depende en el cambio en los pesos de los nodos , que representan la capa de salida. Entonces para cambiar los pesos de la capa oculta, debemos primero cambiar los pesos de la capa de salida de forma acorde a la derivada de la función de activación, y entonces este algoritmo representa una retropropagación de la función de activación.[2]
Compresión de datos
Considérese un MLP de 3 capas, una de entrada, una oculta y la de salida. La capa de entrada está formada por N neuronas, la capa oculta por M (M < N) neuronas y la capa de salida posee N neuronas al igual que la capa de entrada. Se entrena dicho MLP para que cuando se le dé como entrada un vector de datos (x1, x2,..., xN) devuelva ese mismo vector con M datos como salida, con ello estamos enseñando al MLP a transformar un vector de N componentes en uno de M componentes (recordemos que M < N) y a recuperar el vector original a partir del vector "comprimido".
Una vez que el MLP esté entrenado se procede de la siguiente forma:
- Compresión: Para comprimir los datos utilizamos un MLP de dos capas, la de entrada con N neuronas y la de salida con M, los pesos de estas dos capas son los de la capa de entrada y oculta respectivamente, del MLP que entrenamos anteriormente.
- Descompresión: Para descomprimir los datos utilizamos un MLP de dos capas, la de entrada con M neuronas y la de salida con N, los pesos de estas dos capas son los de la capa oculta y la de salida respectivamente, del MLP que entrenamos anteriormente.
El MLP no conseguirá (al menos normalmente) un error nulo durante el entrenamiento, por lo que se trata de un sistema de compresión con pérdidas. Obviamente cuanto mayor queramos que sea el factor de compresión, más error se cometerá.
Reconocimiento de números
Es posible entrenar un perceptrón multicapa para que reconozca un número presente en una imagen de entrada gracias a la librería sklearn en Python. Para ello se puede utilizar la clase MLPClassifier y el dataset MNIST.[3] En el ejemplo se muestra como un simple MLP con 50 capas y un dataset de números de 70.000 imágenes (60.000 para entrenamiento y 10 000 para validación) se puede obtener un score de 0.986800 y 0.970000 sobre los datasets de entrenamiento y testing respectivamente.
Referencias
- Perceptrón multicapa Archivado el 14 de julio de 2014 en Wayback Machine., Redes de Neuronas Artificiales, UC3M, RAI 2012.
- Haykin, Simon (1998). Neural Networks: A Comprehensive Foundation (2 edición). Prentice Hall. ISBN 0-13-273350-1.
- Cursos Python. «Tu primera red neuronal con sklearn, reconociendo imágenes con números». Cursos Python. Consultado el 25 de mayo de 2020.